Матрица сумма по треугольникам

Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .

|А|, ∆ , det A — символы, которыми обозначают определитель матрицы.

Способ вычисления определителя выбирают в зависимости от порядка матрицы.

Определитель матрицы 2-го порядка вычисляют по формуле:

d e t A = 1 — 2 3 1 = 1 × 1 — 3 × ( — 2 ) = 1 + 6 = 7

Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Определитель матрицы 3-го порядка: правило треугольника

Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:

• правило треугольника;
• правило Саррюса.

Как найти определитель матрицы 3-го порядка по методу треугольника?

а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32

А = 1 3 4 0 2 1 1 5 — 1

d e t A = 1 3 4 0 2 1 1 5 — 1 = 1 × 2 × ( — 2 ) + 1 × 3 × 1 + 4 × 0 × 5 — 1 × 2 × 4 — 0 × 3 × ( — 1 ) — 5 × 1 × 1 = ( — 2 ) + 3 + 0 — 8 — 0 — 5 = — 12

Видео:Миноры и алгебраические дополненияСкачать

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

• дописать слева от определителя два первых столбца;
• перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
• перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32

А = 1 3 4 0 2 1 — 2 5 — 1 1 3 0 2 — 2 5 = 1 × 2 × ( — 1 ) + 3 × 1 × ( — 2 ) + 4 × 0 × 5 — 4 × 2 × ( — 2 ) — 1 × 1 × 5 — 3 × 0 × ( — 1 ) = — 2 — 6 + 0 + 16 — 5 — 0 = 3

Видео:Сумма элементов матрицы онлайнСкачать

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:

• разложением по элементам строки;
• разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Разложение матрицы по элементам строки:

d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n

Разложение матрицы по элементам столбца:

d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0

• раскладываем по 2-ой строке:

А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 2 × ( — 1 ) 3 × 1 — 1 3 — 2 5 1 3 1 0 = — 2 × 1 — 1 3 4 5 1 2 1 0 + 1 × 0 — 1 3 — 2 5 1 3 1 0

• раскладываем по 4-му столбцу:

А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 3 × ( — 1 ) 5 × 2 1 0 — 2 4 5 3 2 1 + 1 × ( — 1 ) 7 × 0 1 — 1 2 1 0 3 2 1 = — 3 × 2 1 0 — 2 4 5 3 2 1 — 1 × 0 1 — 1 2 1 0 3 2 1

Видео:МАТРИЦЫ математика УМНОЖЕНИЕ МАТРИЦ и простейшие операции с матрицамиСкачать

Свойства определителя

• если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
• если поменять местами строки и столбцы, то знак поменяется на противоположный;
• определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Пример 6

А = 1 3 4 0 2 1 0 0 5

d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10

Определитель матрицы, который содержит нулевой столбец, равняется нулю.

Видео:Математика это не ИсламСкачать

Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.

Используя этот онлайн калькулятор для вычисления определителя (детерминанта) матриц, вы сможете очень просто и быстро найти определитель (детерминант) матрицы.

Воспользовавшись онлайн калькулятором для вычисления определителя (детерминанта) матриц, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на транспонирование матриц, а также закрепить пройденный материал.

Видео:Сумма элементов матрицы на главной диагоналиСкачать

Найти определитель (детерминант) матрицы

Введите значения Матрицы:

Ввод данных в калькулятор для вычисления определителя (детерминанта) матриц

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления определителя (детерминанта) матриц

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Теория. Определитель (детерминант) матрицы.

Вычисление определителя матрицы 2×2

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

Правило треугольника для вычисления определителя матрицы 3×3

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

+	–

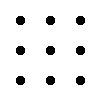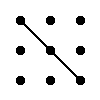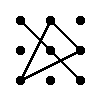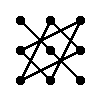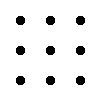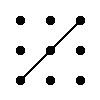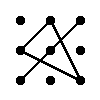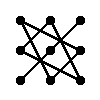Вычисление определителя матрицы произвольного размера

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Определители

Содержание:

Видео:5 способов вычисления определителя ★ Какой способ лучше?Скачать

Определители, их свойства и способы вычисления

Для произвольной квадратной матрицы порядка n можно установить конкретную числовую характеристику, которая носит название определителя (детерминанта) матрицы.

Определитель матрицы обозначают:

— греческой буквой ;

— выражением .

Пример.

В зависимости от размера матрицы (иногда говорят порядка матрицы) определители называют определителями некоторого порядка.

Если порядок матрицы n=1, то её определителем будет сам элемент матрицы, то есть для определитель .

Если порядок матрицы n=2, то есть матрица имеет вид:

то определителем второго порядка, который соответствует такой матрице назовём число, равное

То есть определитель матрицы А будет иметь вид:

Для вычисления определителей матриц более высоких порядков необходимо ввести понятие минора.

Минором произвольного элемента матрицы n-го порядка называют определитель n-1 порядка, который получаем после вычёркивания i-ой строки и j-ого столбца.

Пример. Минорами матрицы А

будут следующие определители:

для элемента

для элемента

для элемента

Минор, взятый вместе со знаком носит название алгебраического дополнения элемента

Знаки алгебраических дополнений чередуются согласно схеме:

в зависимости от расположения элемента

Определитель матрицы n-го порядка равен сумме произведений элементов одной строки или столбца на их алгебраические дополнения.

Запись определителя n-го порядка через его алгебраические дополнения n-1-го порядка называют разложением по i-ой строке или j-ому столбцу.

Например, определитель n-го порядка записанный через разложение по элементам первой строки будет иметь вид:

Пример. Разложить по первой строке определитель 3-го порядка:

Видим, что определитель 3-го порядка разложился на определители 2-го порядка, которые можно вычислить по введённому ранее правилу.

Для определителей 3-го порядка можно воспользоваться мнемоническим правилом, которое значительно упрощает процесс вычисления. Действительно, дописав два первых столбца и перемножив диагональные элементы (см. пример) с соответствующими знаками, получим выражение, которое совпадает с выражением полученным при разложении по минорам:

При вычислении определителей более высокого порядка постепенно разлаживают миноры аж до определителей 2-го порядка.

Очевидно, что при вычислении определителей более высокого порядка удобнее разлаживать по минорам той строки (столбца), в которой больше нулевых элементов (произведение будет равно нулю).

Для достижения такого результата используют свойства определителей.

Свойства определителей

1) то есть определитель не меняется при транспонировании матрицы;

2) если одна строчка определителя состоит только из нулей, то определитель равен нулю (то же самое относится и к столбцам);

3) при перестановке двух строк (столбцов) местами определитель меняет знак;

4) определитель, что содержит две одинаковые строки (столбца) равные нулю;

5) если все элементы некоторой строки определителя умножить на произвольное число k то сам определитель умножится на это же число;

следствие: общий множитель всех элементов строки или столбца можно вынести за знак определителя;

6) определитель, который содержит две пропорциональные строки (столбца) равные нулю;

7) если к элементам одной строки (столбцу) прибавить элементы другой (возможно умноженные на некоторый коэффициент), то определитель не изменится;

8) определитель треугольной матрицы равный произведению элементов, которые расположены на главной диагонали матрицы;

9) определитель произведения матриц равный произведению определителей матриц

Пример 1. Вычислить определитель:

Решение.

Отнимая от первого столбца утроенный последний столбец получим:

Далее определитель разложим по первому столбцу:

Теперь можно воспользоваться приведённым мнемоническим правилом для вычисления определителя 3-го порядка. Можно также продолжить использовать свойства определителей для дальнейшего упрощения выражения. Так, отнимем от 2-го столбца удвоенный 1-ый столбец, получим:

Разложив определитель по первой строке имеем:

Пример 2. Вычислить определитель:

Решение.

Сведём элементы 3-ей строки к нулю, оставив только один ненулевой элемент во втором столбце. Для этого:

— второй столбец умножим на 2 и отнимем от первого

— второй столбец прибавим к третьему

Теперь легко разложить по 3-ей строке:

Можно продолжить использовать свойства определителей для упрощения выражения:

или воспользоваться мнемоническим правилом.

Возможны и другие варианты приведения определителей к удобному для вычисления виду.

Пример 3. Вычислить определитель матрицы АВ, если

Решение.

Вычислим определители матриц А и В:

следовательно, согласно свойствам определителей

Видео:2. Действия над матрицами ( сложение матриц, умножение матрицы на число )Скачать

Понятие определителя и определители второго и третьего порядков

Решение многих экономических задач сводится к решению систем линейных алгебраических уравнений. В основе некоторых методов решения таких систем используются выражения, которые называются определителями (или детерминантами).
Рассмотрим квадратную таблицу из n 2 чисел, размещенных в n-горизонтальных и n-вертикальных рядах. По специальным правилам находится число, которое называют определителем n-го порядка и обозначают буквой «Δ» греческого алфавита:

Числа a_ij (i = 1,2, . n, j = 1,2, . n) называют элементами определителя. Первый индекс указывает номер строки, а второй — номер столбца, на пересечении которых находится элемент. Элементы, в которых оба индекса одинаковы (т.е. элементы a₁₁, a₂₂, . a_nn образуют главную диагональ определителя. Другая диагональ называется побочной
(вспомогательной). Порядок определителя определяет количество его строк (или столбцов).

При вычислении определителей n-го порядка получаем число, равное алгебраической сумме всех возможных произведений его элементов, взятых по одному из каждого из n строк и каждого из n столбцов. При этом половина слагаемых имеют свои знаки, а другая — противоположные.

Покажем, как вычисляются определители второго и третьего порядков. Для уточнения понятия «определитель» рассмотрим два линейных уравнения с двумя неизвестными с буквенными коэффициентами:

Для решения этих уравнений мы должны умножить их на соответствующие коэффициенты, при которых исключается одно из неизвестных:

В зависимости от используемой пары множителей (по вертикали) исключаем или x₁ или x₂ и получим такие уравнения:

Отсюда

Эти выражения имеют смысл только при условии, если знаменатель не равен нулю.
Если, a₁₁ a₂₂ – a₁₂ a₂₁ = 0, то система уравнений либо не имеет решения, либо имеет бесконечное множество решений. Коэффициенты при неизвестных образуют выражения, которые называются определителями.

Рассматривая эти коэффициенты, мы видим, что они одинаковы при обоих неизвестных; состоят из двух произведений, каждое из которых включает два элемента.
Определители второго порядка символически обозначаются так:

Определителем второго порядка называется число, которое равно разнице произведений элементов главной и вспомогательной диагоналей, то есть

Это иллюстрируется схемой:

Пример 1. Вычислить определитель второго порядка:
Решение. По предыдущей формуле находим:

Определителем третьего порядка называется число, которое находится по формуле

Знаки, которые стоят перед каждым из слагаемых, следует выбирать по следующей схеме:

Это правило вычисления определителей 3-го порядка называется правилом треугольников. Здесь слагаемые со знаком «+» являются произведениями элементов, которые стоят на главной диагонали определителя a₁₁, a₂₂, a₃₃ и произведения элементов, стоящих в вершинах треугольников с основаниями, параллельными главной диагонали a₁₂, a₂₃, a₃₁ и a₁₃, a₂₁, a₃₂. Со знаком «–» берутся слагаемые, которые являются произведениями элементов побочной диагонали a₁₃, a₂₂, a₃₁ и произведения элементов вершин треугольников с основаниями, параллельными этой диагонали определителя a₁₂, a₂₁, a₃₃ и a₁₁, a₂₃, a₃₂.

Пример 2. Вычислить определитель

Решение. Пользуясь правилом треугольников, получим

Правило треугольников легко запомнить, если дописать рядом с определителем первый, а затем второй его столбцы. Произведения элементов, которые находятся на диагоналях, отмеченных на схеме сплошными линиями, берутся со знаком «+», a произведения элементов, которые находятся на диагоналях, обозначенных на схеме пунктиром, со знаком «–» . Алгебраическая сумма этих шести произведений и дает значение определителя

Такой способ вычисления определителя третьего порядка называется правилом Саррюса.
Вычислим предыдущий определитель 3-го порядка по правилу Саррюса.

При вычислении определителей используют их свойства, которые рассматриваются в следующем параграфе.

Замечание. Определителем первого порядка является число, которое равно этому элементу, то есть . Поэтому не следует путать обозначение определителя с модулем самого числа.

Свойства определителей

Определители произвольного порядка обладают рядом свойств.
Свойство 1. Если в определителе поменять местами строки на столбцы, то величина определителя не изменится:

Доказательство. Для определителя второго порядка имеем:

Замену в определителе строк на соответствующие столбцы называют транспонированием определителя.

Пример 1. Проверим справедливость свойства на примере определителя третьего порядка:

Поменяем местами строки на столбцы:

Следовательно, величина определителя не меняется при его транспонировании, то есть его строки и столбцы равноправны.

Свойство 2. Если в определителе поменять местами две строки (или столбца), то он изменит только знак, не меняя абсолютной величины.

Доказательство. Поменяем местами строки в определителе второго порядка:

Пример 2. Поменяем местами первую и третью строки определителя третьего порядка из примера 1.

Итак,

то есть имеет место свойство 2.

Свойство 3. Если в определителе все элементы произвольной строки (или столбца) равны нулю, то определитель равен нулю:

i-я строка

Доказательство. Доказательство этого свойства очевидно, поскольку при вычислении определителя все слагаемые содержат нулевые множители i-й строки. Поэтому и сам определитель равен нулю.

Свойство 4. Если в определителе есть две одинаковые строки (или столбца), то определитель равен нулю.

Доказательство. Для доказательства этого свойства поменяем местами i-ю и k-ю строки. С одной стороны, величина определителя не изменится (поскольку одинаковые строки), а с другой — изменится знак на противоположный (согласно свойству 2). Если обозначить величину определителя через Δ, то получим равенство Δ = –Δ, то есть 2Δ = 0, а значит Δ = 0.

Пример 3. Определитель третьего порядка равен нулю:

поскольку он имеет два одинаковых столбца.

Свойство 5. Если все элементы произвольной строки (или столбца) имеют общий множитель, то его можно вынести за знак определителя:

Доказательство. Пусть все элементы i -й строки определителя имеют общий множитель . Поскольку определитель равен сумме произведений элементов, в т. ч. рассматриваемой i -й строки, то можно вынести из этой суммы за скобки. Если записать выражение в скобках в виде определителя, то получим предыдущее равенство.

Следствие. Если произвольную строку (или столбец) определителя умножить на число , то величина определителя изменится в раз.

В частности, если элементы, например, первой строки определителя второго порядка имеют общий множитель ««, то

Пример 4. В определителе третьего порядка

элементы первой и второй строк имеют общие множители «2» и «4», поэтому их можно вынести за знак определителя

Свойство 6. Если в определителе элементы одной строки (или столбца) пропорциональны соответствующим элементам другой строки (или столбца), то определитель равен нулю:

Доказательство. Пусть элементы i-й и k-й строк пропорциональны. По свойству 5 постоянный множитель пропорциональности можно вынести за знак определителя. При этом получим произведение числа на определитель с двумя одинаковыми строками, равный нулю (по свойству 4).

Пример 5. Определитель третьего порядка

потому что первая и вторая строки пропорциональны.

Свойство 7. Если в определителе все элементы произвольной строки (или столбца) являются суммой двух слагаемых, то определитель можно представить в виде суммы двух определителей. При этом элементы рассматриваемой строки (или столбца) в первом определителе являются первыми слагаемыми, а элементы соответствующей строки (или столбца) второго определителя — вторыми слагаемыми:

Доказательство. Докажем справедливость этого свойства на примере определителя второго порядка:

Пример 6. Вычислить определитель:

Элементы, например, второй строки можно представить в виде суммы двух слагаемых:

= (–18 + 2 + 0 + 0 – 8 – 6) + (–12 + 2 + 0 + 0 – 8 – 3) = –30 – 21 = –51.

Свойство 8. Величина определителя не изменится, если к элементам произвольной строки (или столбца) добавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число :

Доказательство. Для доказательства представим определитель правой части согласно свойству 7 в виде суммы двух определителей:

Во втором определителе правой части элементы i-й строки пропорциональны соответствующим элементам k-й строки, поэтому по свойству такой определитель равен нулю. Следовательно, имеет место свойство 8.

Пример 7. Вычислить определитель

Здесь мы к элементам третьей строки добавили соответствующие элементы первой строки, умноженные на число «–3».

В дальнейшем, свойство 8 используется для вычисления определителей высших порядков. При этом в произвольной строке (или столбце) образуем все нули, кроме одного элемента.
Пусть имеем определитель n — го порядка (n > 3);

Δ =

Определение 1. Минором M_ij элемента a_ij определителя n-го порядка называется определитель (n – 1)-го порядка, полученный сиз предыдущего после вычеркивания i-й строки и j-го столбца, на пересечении которых находится данный элемент.

Определение 2. Алгебраическим дополнением A_ij элемента aij определителя n-го порядка называется минор для этого элемента, взятый со знаком «+», если число (i + j) — четное и со знаком «–», если оно нечетное. То есть A_ij = (-1) i+j M_ij.

Пример 8. Найти алгебраические дополнения к элементам a₁₃ и a₃₂ определителя

Алгебраические дополнения A₁₃ и A₃₂ найдем по предыдущей формуле:

Согласно определению 1 имеем:

Искомые алгебраические дополнения будут A₁₃ = 6, A₃₂ = –18.

Свойство 9. (Теорема Лапласа).
Определитель равен сумме произведений элементов произвольной строки (или столбца) на соответствующие алгебраические дополнения:

(1.1)
Эта теорема называется еще теоремой разложения. При этом первая формула является разложением определителя по элементам его строки, а вторая — разложением определителя по элементам его столбца.

Доказательство. Докажем это свойство для определителя третьего порядка:

Таким образом,

Это формула разложения определителя по элементам первой строки. Аналогично можно найти разложение определителя по элементам второй строки или произвольного столбца.

С помощью этого свойства, вычисление определителя n-го порядка сводится к вычислению определителей (n – 1)-го порядка. Поэтому при вычислении таких определителей лучше выбирать для разложения строку или столбец, в котором есть нули. При этом будем вычислять не n определителей (n – 1)-го порядка, а меньше.

Пример 9. Вычислить определитель 3-го порядка, разложив его по элементам первой строки:

=

Замечание. Данный определитель проще было бы вычислять, разложив его по элементам третьей строки (или третьего столбца), поскольку одно из слагаемых не нужно вычислять (элемент a₃₃ = 0).

Следствие 1 (Теорема замещения).
Пусть A_i1, A_i2, . A_in — алгебраические дополнения элементов i-й строки определителя n-го порядка.
Δ =
Тогда сумма произведений алгебраических дополнений элементов i-й строки на произвольные числа b₁, b₂, . b_n равна такому определителю n-го порядка Δ’ , у которого элементами i -й строки являются числа b₁, b₂, . b_n, а остальные — совпадают с соответствующими элементами определителя Δ.

Здесь

где правая часть образовалась после разложения определителя n-го по строке с элементами i -й строки. Это и доказывает теорему.

Аналогично, сумма произведений алгебраических дополнений элементов j-го столбца на произвольные числа b₁, b₂, . b_n то есть b₁ A_1j + b₂ A_2j + . + b_n A_nj равно определителю Δ’, элементами j-го столбца которого являются числа 1 февраля b₁, b₂, . b_n, а остальные элементы совпадают с соответствующими элементами определителя Δ.

Следствие 2 (Теорема аннулирования).
Сумма произведений элементов произвольной строки (или столбца) на алгебраические дополнения параллельной другой строки (или столбца) равна нулю.

Доказательство. В определителе Δ выделим две строки — i-ю и k-ю.

Найдем сумму произведений элементов i-й строки на алгебраические дополнения элементов k-й строки:
a_i1 A_k1 + a_i2 A_k2 + . + a_in A_kn.
По теореме замещения эту сумму можно заменить определителем с двумя одинаковыми
строками

Полученный определитель имеет две одинаковых строки, а потому равен нулю.

Пример 10. Пользуясь свойствами определителей, вычислить.
Δ =
Решение. Добавим элементы первого и второго столбцов, а от элементов третьего столбца вычтем удвоенные элементы первого. Получим:
Δ =

Пример 11. Вычислить определитель, использовав его свойства:
Δ =
Решение. Вынесем за знак определителя общий множитель «8» первого столбца и общий множитель «7» второй строки
Δ = 8 ⋅7 ⋅
Вычтем из элементов первой строки удвоенные соответствующие элементы второй строки. К элементам третьей строки добавим соответствующие элементы второй строки, умноженные на число «–5»:
Δ = 8 ⋅ 7 ⋅
Такой определитель легко вычислить, разложив его по элементам первого столбца:
Δ =

Вычисление определителей произвольного порядка

Определителем n-го порядка называется число, равное сумме произведений элементов произвольной строки или столбца, на соответствующие алгебраические дополнения.

При этом имеют место формулы разложения определителя по элементам его произвольной строки (или столбца) (1.1).

Определение определителя n-го порядка взято как метод его вычисления.

Пример 1. Вычислить определитель 4-го порядка:

Решение. Разложим определитель по элементам второй строки:

Каждый из этих определителей вычислим, еще раз использовав формулу Лапласа. Первый и третий определители разложим по элементам второй строки:

Четвертый определитель разложим по элементам третьей строки:

Итак,
Δ = 1⋅ (–1) 3 ⋅ 3 + 1⋅ (–1) 5 ⋅63 + 2 ⋅ (–1) 6 ⋅ 21 = –3 – 63 + 42 = –24.

Как видим, вычисление определителя 4-го порядка сводится к вычислению четырех определителей 3-го порядка, а вычисление определителя 5-го порядка — к вычислению пяти определителей 4-го порядка или двадцати определителей 3-го порядка. Поэтому целесообразно сначала преобразовать определитель так, чтобы в одной из строк (или столбцов) все элементы, кроме одного, стали нулевыми. Этого можно достичь, использовав свойства определителей.
Таким образом, вычисления определителя n-го порядка сводится к вычислению только одного определителя (n –1)-го порядка.

Пример 2. Вычислить определитель, использовав его свойства:

Δ =
Решение. От элементов третьего столбца вычтем соответствующие элементы первого столбца, а к элементам четвертого столбца добавим соответствующие элементы первого столбца, умноженные на «–2».
Δ =
Полученный определитель 3-го порядка можно вычислить, например, по правилу Саррюса, или свести к определителю 2-го порядка, отняв от элементов второго и третьего столбцов
соответствующие элементы первого столбца
Δ =
Получили значительно более легким путем тот же результат определителя.

Пример 3. Вычислить определитель 5-го порядка

Δ =
Решение. Добавим к элементам первого столбца соответствующие элементы третьего столбца, умноженные на «–2», а от элементов четвертого столбца вычтем утроенные элементы третьего и от пятого — вычтем элементы третьего. В результате получим
Δ =
Добавим к элементам первого столбца соответствующие элементы четвертого столбца, умноженные на «5», от элементов второго столбца вычтем соответствующие элементы четвертого столбца, а к элементам третьего столбца добавим соответствующие элементы четвертого столбца, умноженные на число «4».
Δ =
Добавим к элементам второй строки удвоенные элементы первой строки:

Итак, определитель Δ = -264.
Определитель n-го порядка можно вычислить, сведя его к треугольному виду.

Определение. Определителем треугольного вида называется определитель, у которого ниже (или выше) главной диагонали все нулевые элементы, то есть:

ТЕОРЕМА. Определитель треугольного вида равен произведению диагональных элементов.

Доказательство. Действительно, поскольку определитель равен алгебраической сумме произведений его элементов, взятых по одному из каждой строки и каждого столбца, то единственным отличным от нуля слагаемым является произведение элементов, которые стоят по главной диагонали:
Δ₁ = Δ₂ = a₁₁ ⋅ a₂₂ ⋅ a₃₃ ⋅ . ⋅ a_nn.
Произвольный определитель можно свести к определителю треугольного вида, использовав его свойства.

Пример 4. Вычислить определитель третьего порядка, сведя его к треугольному виду:

Δ =
Решение. Поменяем местами элементы первой и третьей строк, изменив знак перед определителем на противоположный:

Δ =
Добавим к элементам второй и третьей строк соответствующие элементы первой строки, умноженные соответственно на «–3» и «–2»:
Δ =
Из третьей строки вынесем общий множитель «–3» за знак определителя и одновременно поменяем местами вторую и третью строки. При этом перед определителем знак изменится на противоположный:

Δ =
Добавим к элементам третьей строки соответствующие элементы второй строки, умноженные на «6».
Δ =
Отсюда получим Δ = –3 ⋅ 1⋅ 1⋅ 1 = –3.

Пример 5. Вычислить определитель пятого порядка:
Δ =
Решение. Поменяем местами две первые строки, изменив знак перед определителем на противоположный:

Δ =
Добавим к элементам второй, третьей и четвертой строк соответствующие элементы первой строки, умноженные соответственно на «–2», «–4», «–3». Получим:

Δ =
Добавим к элементам третьей и четвертой строк соответствующие элементы второй строки, умноженные на «–7» и «–2 «:

Δ =
Если добавить элементы третьей и четвертой строк, то определитель будет треугольного вида:

Δ =
который равен произведению элементов главной диагонали:
Δ = (-1) ⋅ (-1) ⋅ 4 ⋅ 40 = 160.

Определители второго и третьего порядков

Каждой квадратной матрице А размерности по определенному закону ставится в соответствие некоторое число (читается «дельта а»), называемое определителем матрицы А. Т.к. мы условились, что такие матрицы имеют порядок , то и определитель будет иметь порядок . Часто вместо слова «определитель» говорят «детерминант». Другие обозначения определителя или .

Определитель 2 —го порядка вводится с помощью формулы:

(1)

а определитель 3-го порядка — формулой

(2)

Для запоминания (2) удобно пользоваться схемой:

На левой половине схемы соединены линиями каждые три элемента определителя, произведение которых входит в правую часть (2) со знаком «+». На правой части схемы показаны произведения, входящие со знаком «-».

Для запоминания (2) часто применяют и правило Саррюса. К основному определителю дописывают первые два столбца и действуют по следующей схеме:

Определители порядка n

Перейдем теперь к общему случаю — рассмотрим определитель порядка :

Определение 1. Минором элемента называется определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих . Алгебраическим дополнением элемента называется минор взятый со знаком ,т.е.

Например, для определителя

Используя понятие алгебраического дополнения, непосредственной проверкой можно убедиться в том, что (1) может быть записана, как

(3)

(4) Формулы (3), (4) наводят на мысль о характере общего определения, которое можно дать определителю порядка .

Определение 2. Определителем матрицы А называется сумма произведений элементов первой строки на их алгебраические дополнения:

(5)

Заметим, что определение 2 дает и способ вычисления определителей любого порядка. Оказывается, что справедлив и более общий результат.

Теорема 1 (основная теорема об определителях). Определитель равен сумме произведений элементов любой строки на их алгебраические дополнения.

Свойства определителей

Результат, сформулированный как теорема 1, позволяет раскладывать определители порядка по строке. Это приводит к вычислению ряда миноров, т.е. определителей порядка ( -1) и т.д. Т.о., если — достаточно большое число, то процедура вычисления может оказаться громоздкой. Однако, ее можно сильно упростить, если знать свойства определителей.

Основными свойствами определителей являются следующие:

1. Если все элементы некоторой строки равны нулю, то определитель равен нулю.

2. При перестановке двух строк местами знак определителя изменяется на противоположный.

3. Определитель с двумя одинаковыми строками равен нулю.

4. Общий множитель всех элементов строки можно выносить за знак определителя.

5. Если элементы некоторой строки определителя представлены в виде суммы двух слагаемых, то и сам определитель равен сумме двух определителей и . В определителе указанная строка состоит из первых слагаемых, а в — из вторых слагаемых. Остальные строки определителей и — те же, что и в .

6. Если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже число, то определитель не изменится.

7. Сумма произведений элементов произвольной строки на алгебраические дополнения элементов другой строки равна нулю.

8. Определитель при транспонировании матрицы не изменяется.

Замечание 1. Решение значительно упрощается, если в строке, по которой раскладывается определитель, имеется возможно большее число нулей. Этому можно способствовать, используя свойства определителей.

Замечание 2. Из свойства 8 следует, что любое из свойств определителя остается справедливым, если в формулировках слово «строка» заменить всюду на слово «столбец». В частности, можно сформулировать и аналог теоремы 1.6.

Пример №28

Вычислить определитель матрицы :

Решение:

Используя свойства определителей и основную теорему 1.6, получим

Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:

Другие темы которые вам помогут понять высшую математику:

Видео:Определитель матрицы 3 порядка. Как легко найти? Метод треугольников и Саррюса. Просто и наглядноСкачать

Определители: определения и методы вычисления

В линейной алгебре определи́тель (или детермина́нт) — это скалярная величина, которая обозначает ориентированное «растяжение» или «сужение» многомерного евклидового пространства после преобразования матрицей: детерминант имеет смысл только для квадратных матриц.

Определение определителя. Определители 2-го и 3-го порядков

Одним из видов числовых матриц, которые часто используются при построении математических моделей экономических задач являются квадратные матрицы. Таким матрицам ставится в соответствие числовая характеристика — определитель, или детерминант, который обозначают rрецькою буквой со ссылкой на соответствующую матрицу: (или без него), а также (от лат. determinans — определяющий).

Прежде, чем дать определение детерминанта, введем к рассмотрению некоторые вспомогательные понятия. Пусть задано конечное множество с первых натуральных чисел . Кроме естественного расположения чисел (по возрастанию), иx можно упорядочить и многими другими способами. Любое расположение чисел в некотором определенном порядке называется перестановкой чисел, а сами числа называют элементами перестановки. (Число различных перестановок чисел равно произведению , которое обозначается через и читается эн-факториал.) Рассмотрим два произвольные элементы и перестановки элементов (). Говорят, что элементы и образуют инверсию (от греч. inversio — переворачивание, перестановка), если , но в перестановках предшествует, то есть нарушается порядок расположения цифр по возрастанию. Перестановки называется пapним (нечетным), если оно имеет в себе парное (нечетное) число инверсий. Числа, которые образуют перестановки, обычно берутся в круглые скобки.

Так, перестановки из четырех цифр: (3, 1, 4, 2), содержит три инверсии; иx образуют три пары цифр: (3,1), (3,2) и (4,2), то есть эта перестановка являются нечетной. Перестановка (4, 2, 1, 3) содержит четыре инвepcии: (4,2), (4,1), (4,3) и (2,1), так она есть четной.

Определителем, или детерминантом, -гo порядка матрицы называется число, которое равняется алгебраической сумме слагаемых вида , каждый из которых является произведением элементов матрицы, выбранных по одному и только по одному из каждой строки и каждого столбца, при этом произведение берется со своим (с противоположным) знаком, если перестановка с вторых индексов элементов является парным (нечетным):

где — количество инверсий в перестановках , образованных из вторых индексов элементов матрицы при условии, что первые индексы расположены в порядке возрастания.

Определители изображают, как и матрицу, в виде таблицы чисел, но в прямых скобках (а не в круглых или в квадратных):

Слагаемые алгебраической суммы (2.1) называются членами определителя.
Для лучшего осмысления приведенного определения рассмотрим детерминанты второго и третьего порядков.

Согласно с определения детерминант 2-гo порядка равен сумме произведения элементов главной диагонали, взятом со знаком плюс, и произведения элементов побочной диагонали, взятом со знаком минус, поскольку перестановка из вторых индексов элементов первого члена не содержит инверсий: (1, 2), а перестановка из вторых индексов элементов второго члена — одну инверсию: (2, 1).

Справа в (2.2) приведено геометрическую схему, по которой исчисляется . На ней элементы определителя обозначены кружками, а отрезками соединены элементы, которые находятся в разных строках и разных столбцах.

По определению (2.1) детерминант третьего порядка имеет шесть членов: и вычисляется по формуле:

Справа в (2.3) изображена геометрическая схема, по которой исчисляется определитель 3-го порядка, ее называют правило треугольников. На этой схеме, как и выше, элементы определителя обозначены кружками, а отрезки соединяются элементами, которые находятся в разных строках и разных столбцах; они определяют шесть треугольников (по количеству членов детерминанта).

В первой тройке членов перестановки из вторых индексов элементов парные, поэтому каждый из них берется со знаком плюс, а во второй — нечетные, поэтому каждый берется со знаком минус.

Замечания. Определителем 1-гo порядка матрицы является сам элемент, из которого он состоит:

Вычислим определитель 3-го порядка:

Количество членов детерминанта быстро растет с увеличением его порядка. Например, вычисления определителя четвертого порядка требует подсчета двадцати четырех его членов: , а при уже есть .

Рядом со словосочетанием вычисление определителя используют раскрытия определителя, как синоним.

Свойства определителей

Рассмотрим свойства определителей, которые целесообразно использовать для упрощения процесса их вычисления.

1 (о определителе транспонированной матрицы). Определитель транспонированной матрицы равный определителю исходной матрицы :

Это свойство указывает на равноправие строк и столбцов определителя, поэтому при дальнейшем рассмотрении мы будем формулировать свойства определителя относительно действий над строками, но те же свойства распространяются и на действия над столбцами.

2 (об изменении знака). Если в определителе поменять местами две строки, то получим определитель, который имеет противоположный знак:

где и — номера двух строк, которые меняются местами.

3 (о общем множителе элементов строки). Если элементы некоторой строки определителя содержат общий множитель , то его можно вынести за знак (символ) определителя:

Свойство 3 предполагает другую формулировку: если все элементы любой строки определителя умножить на некоторое число , то выходной определитель умножится на .

4 (о равенстве определителя нулю). Определитель равен нулю, если: а) все элементы некоторой строки равны нулю:

б) он содержит две или более строк с одинаковыми или пропорциональными элементами:

5 (о представлении определителя в виде суммы двух определителей). Если элементы любой строки определителя (пусть это будет -я строка) является суммой двух слагаемых, то этот определитель можно представить в виде суммы двух определителей того же порядка, в которых элементы всех строк, кроме -гo, являются элементами исходного определителя, а элементами их -x строк является слагаемые -й строки заданного определителя:

6 (об инвариантности, то есть неизменность определителя). Определитель не изменится, если к элементам любой его строки добавить соответствующие (по номеру) элементы другой строки, умноженные на одно и то же число :

действительно по предварительному свойству получаем сумму двух определителей, первый из которых равен , а второй, содержащий две строки с пропорциональными элементами и по свойству (4 б) равен нулю.

Как одно из свойств определителей приведем теорему Лапласа, которая является частным случаем более общей теоремы. Она имеет важное теоретическое значение и применяется при исчислении определителей, порядок которых больше трех. Для ее формулировки и доказательства необходимо обозначить новые понятия.

Минором элемента определителя -го порядка (от лат. minor — меньше) называется определитель ( -1) -го порядка, который получают из исходного определителя исключением -й строки и -го столбца, на пересечении которых расположен данный элемент. Он обозначается .

Алгебраическим дополнением элемента определителя -гo порядка называют его минор, взятый со знаком «плюс», если сумма индексов () является четным числом, и со знаком минус», если эта сумма индексов нечетная. Он обозначается :

Определим минор и алгебраическое дополнение элемента определителя

Изымаем из исходного определителя первую строчку и второй столбец, на пересечении которых расположен элемент , и вычисляем определитель 2-го порядка. Поскольку для элемента сумма индексов является нечетной, то минор и алгебраическое дополнение этого элемента отличаются знаком:

Введены понятия используются для установления важных утверждений относительно обоснования внедрений матриц и определителей к решению прикладных задач.

Теорема 2.1 (теорема Лапласа о раскрытии определителя). Определитель -го порядка равен сумме произведений элементов любой строки или столбца с их алгебраическими дополнениями:

Доказательство проведем для , исходя из формулы (2.3):

Сгруппируем попарно члены определителя относительно элементов первой строки:

Выражения в круглых скобках с учетом знака слагаемых являются алгебраическими дополнениями элементов

Аналогично проводят доведения (2.12) для произвольного , произвольных строк и столбцов.

Следствие. Сумма произведений элементов любой строки (столбца) с алгебраическими дополнениями соответствующих (по номеру) элементов другой строки или столбца равна нулю:

Видео:Обратная матрицаСкачать

Способы вычисления определителей

Рассмотрим на примерах способы вычисления определителей.

Применение теоремы Лапласа

Вернемся к примеру, который рассматривался ранее, и вычислим определитель 3-гo порядка по теореме Лапласа.

Обратите внимание на то, что , поэтому целесообразно осуществлять разложение определителя по элементам или первой строки или второго столбца, поскольку в этих случаях будем иметь только два слагаемых. Если раскладывать по элементам первой строки, то получаем:

Результаты вычислений по определению (2.3) и по теореме Лапласа (2.12) совпали.

По теореме Лапласа вычисления определителя -го порядка можно всегда свести к вычислению определителей -го порядка, количество которых составляет и дальше, пока не дойдем до определителей первого порядка — элементов исходного определителя.

Применение теоремы Лапласа с привлечением свойства об инвариантности определителя

Понятно, что объем вычислений по формуле (2.12) уменьшается, ежели некоторые из элементов выбранной строки равны нулю, поскольку соответствующие им алгебраические дополнения нет необходимости вычислять. Свойство 6 (об инвариантности определителя) позволяет получить все элементы произвольного строки или столбца равными нулю, кроме одного. Элемент , который остается отличным от нуля, называется ведущим элементом, а соответствующая строка с номером (или столбец ), в котором стоит и с помощью которого как раз и осуществляются преобразования, тоже называется ведущим.

Вычислим определитель четвертого порядка:

Второй столбец определителя уже содержит ноль , а йоrо элемент возьмем ведущий, и сделаем нулями все остальные элементы второго столбца. Поскольку первая строка является ведущим, то его элементы оставляем без изменения, а к элементам второй строки добавляем соответствующие элементы першего, умноженные на . К элементам четвертой строки добавляем соответствующие элементы первого, умноженные на :

Теперь раскрываем определитель по элементам второго столбца получаем вместо определителя четвертого порядка один определитель третьего порядка:

С первой строки выносим множитель (-1) и получим определитель:

Аналогично сводим вычисления полученного определителя к вычислению определителя 2-го порядка. Для этого возьмем элемент по проводной. Вторую строчку определителя оставим без изменения, а к элементам первой строки добавим соответствующие элементы второго, помноженные на (-7), а к элементам третьей строки — элементы второго, помноженные на 19:

Теперь раскрываем этот определитель по элементам третьего столбца и получаем определитель второго порядка, вычисляем по определению:

Применение теоремы Лапласа к вычислению определителя треугольной матрицы

Определитель верхней треугольной матрицы последовательно раскрывают по элементам 1-го столбца каждого с определителей, которые для такой матрицы являются алгебраическими дополнениями элементов главной диагонали. Тогда выходной определитель получим в виде произведения элементов его главной диагонали:

Такую же формулу получим для вычисления определителя нижней треугольной матрицы, если на каждом шагу раскрывать по элементам первой строки алгебраические дополнения диагональных элементов.

Рассмотрим этот способ на примере:

Таким образом, для вычисления определителя -го порядка можно применять несколько способов, которые упрощают вычисления. Все они опираются на свойства определителя, а выбор определенного способа зависит от исследователя.

Обратная матрица

Квадратная матрица называется неособенной или невырожденной, если ее определитель не равен нулю: . В противном случае она называется особой, или вырожденной.

Матрица , транспонированная к матрице, составленной из алгебраических дополнений элементов матрицы , называется присоединенной или союзной, к матрице :

Матрица называется обратной к матрице , если произведение этой матрицы с матрицей как слева, так и справа равна единичной матрицы:

Теорема 2.2 (существования и единственности обратной матрицы). Любая неособенная матрица имеет обратную матрицу , и притом только одну.

Доказательство. Пусть матрица является неособенной. Разделим элементы союзной матрицы на определитель исходной матрицы (это можно сделать, поскольку ) и получим:

Докажем, что матрица, которую определяет соотношение (2.14), является обратной к матрице , то есть по определению для нее выполняются равенства:

Для этого рассмотрим произведение матриц:

Действительно, сумма произведений элементов -й строки матрицы и соответствующих элементов -го столбца матрицы согласно теореме Лапласа равен определителю матрицы при, а при это произведение равно нулю.
Итак, произведение матрицы с матрицей дает единичную матрицу.

Аналогичный результат получим, если будем рассматривать произведение

Предположим теперь, что существует матрица , отличная от , для которой тоже выполняется соотношение . Тогда на основании ассоциативности умножения матриц приходим к противоречию:

Таким образом, матрица не может быть отличной от матрицы . Обратные матрицы используются как в теоретических исследованиях, связанных со свойствами матриц, так и в прикладных задачах.

Найдем матрицу. Обратную к матрице

Убедимся в том, что матрица является невырожденной. Для этого вычислим ее определитель:

Поскольку , то обратная матрица существует. Находим алrебраьiчнi дополнение всех элементов исходной матрицы:

Записываем союзную и обратную матрицы:

Проверим правильность полученного результата:

Решение системы линейных уравнений по правилу Крамера

Определители -го порядка применяются при решении систем линейных уравнений с неизвестными:

Теорема 2.3 (правило Крамера). Если определитель -го порядка основной матрицы системы отличен от нуля , то она имеет единственное решение, который находится по формуле:

где — определитель, полученный из определителя основной матрицы системы заменой -го столбца столбцом свободных членов :

Доказательство. Покажем справедливость формулы (2.16) для = 1. Для этого умножьте в левую и правую части -гo уравнения системы (2.15) на алгебраическое дополнение элемента первого столбца определителя основной матрицы системы и запишем сумму преобразованных таким образом уравнений:

В полученном уравнении коэффициент при неизвестном есть расписанию определителя основной матрицы системы с элементами первого столбца, а коэффициенты при равны нулю (согласно следствием из теоремы Лапласа). Свободный член есть расписанию определителя по элементам первого столбца. Таким образом , уравнение (2.17) имеет вид: . Отсюда

Аналогично выводим формулу (2.16) для других неизвестных.

Замечания. Правило Крамера исключает из рассмотрения случай, когда

С формулы (2.16) следует:

1) если , но хотя бы один из определителей отличный от нуля, то система несовместима, так по крайней мере один из дробей в (2.16) теряет смысл;
2) если и то система неопределенная и имеет множество решений.

Рассмотрим решения СЛАУ по правилу Крамера:

Вычислим определитель основной матрицы системы:

Поскольку матрица является невырожденной, то система уравнений имеет единственное решение. Вычисляем определители, соответствующие неизвестным:

По правилу Крамера находим решение системы:

Итак, решением системы является тройка чисел:

Решение системы линейных алгебраических уравнений методом обратной матрицы

Запишем систему линейных уравнений в матричной форме (1.8):

Решим это матричное уравнение относительно матрицы неизвестных . Будем рассматривать случай, когда основная матрица системы является невырожденной, то есть для нее существует обратная. тогда:

умножаем обе части уравнения слева на

применяем соединительный закон применим определения обратной матрицы и свойство единичной:

Следовательно, если существует обратная матрица к основной матрице системы, то решение СЛАУ, содержащее уравнений относительно неизвестных, можно найти с помощью обратной матрицы в виде:

Решим СЛАУ, которая состоит из трех уравнений относительно трех неизвестных, по методу обратной матрицы:

Обратная матрица существует, поскольку определитель основной матрицы системы не равен нулю:

Определим алгебраические дополнения и построим союзную матрицу :

Умножив матрицу на постоянную , получим обратную матрицу:

Проверим правильность вычислений:

Следовательно, обратная матрица найдена правильно.

Теперь находим решение системы по формуле (2.18):

Таким образом, решением данной системы будет единственная тройка цифр:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

📸 Видео

Как найти определитель матрицы 2х2, 3х3 и 4х4Скачать

Как найти сумму матриц онлайн. Пример с решениемСкачать

Сумма и разность матриц, умножение матрицы на числоСкачать

Двумерный массив. Элементы главной диагонали. СуммаСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Умножение матрицСкачать

Как найти ранг матрицы (пример) - bezbotvyСкачать

Обратная матрица (2 способа нахождения)Скачать