 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
- Вписанные и центральные углы
- Теоремы о вписанных и центральных углах
- Теоремы об углах, образованных хордами, касательными и секущими
- Доказательства теорем об углах, связанных с окружностью
- Внутренние накрест лежащие углы
- Геометрия. Урок 2. Углы
- Понятие угла
- Виды углов:
- Биссектриса угла
- Углы, образованные при пересечении двух прямых
- Углы, образованные при пересечении двух прямых секущей
- Сумма углов многоугольника
- Примеры решений заданий из ОГЭ
- 📽️ Видео
Видео:УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
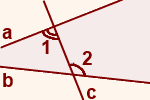
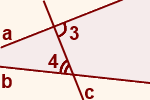
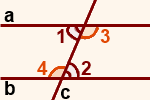
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Накрест лежащие углы⚔️Скачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Пары углов в геометрииСкачать  Внутренние накрест лежащие углыВнутренние накрест лежащие углы — один из видов углов, образованных при пересечении двух прямых секущей. Две прямые разбивают плоскость на внутреннюю (внутри между прямыми) и внешнюю области. Углы, лежащие во внутренней части, так и называются — внутренние. Внутренние накрест лежащие углы — это углы, которые лежат во внутренней области по разные стороны от секущей (накрест друг от друга). При пересечении двух прямых секущей образуется две пары внутренних накрест лежащих углов. ∠1 и∠2 — внутренние накрест лежащие углы при прямых a и b и секущей c. ∠3 и∠4 — внутренние накрест лежащие углы при прямых a и b и секущей c. Из всех внутренних накрест лежащих углов наибольший интерес представляют углы при параллельных прямых. Свойство параллельных прямых Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны. ∠1 = ∠2 ∠3 = ∠4 (как внутренние накрест лежащие углы при a ∥ b и секущей c). Признак параллельных прямых Если внутренние накрест лежащие углы равны, то прямые параллельны. А так как эти углы — внутренние накрест лежащие при прямых a и b и секущей c, то a ∥ b (по признаку параллельных прямых). Равенство внутренних накрест лежащих углов при параллельных прямых используется, в частности, при доказательстве равенства треугольников и подобия треугольников. Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать  Геометрия. Урок 2. УглыСмотрите бесплатные видео-уроки на канале Ёжику Понятно. Видео-уроки на канале Ёжику Понятно. Подпишись! Содержание страницы:
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Понятие углаУгол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Стороны угла – лучи, которые образуют угол. Вершина угла – точка, из которой выходят лучи. Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла. Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O . Величину угла измеряют в градусах. ∠ A O B = 24 ° . Видео:Параллельные прямые | Математика | TutorOnlineСкачать  Виды углов:Видео:Накрест лежащие, односторонние и соответственные углы. Геометрия 7 классСкачать  Биссектриса углаБиссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла. Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла. O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла. ∠ A O D = ∠ B O D = ∠ A O B 2 Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B . Видео:Вариант 11, № 1. Внутренние накрест лежащие углы. Пример 1Скачать  Углы, образованные при пересечении двух прямыхВертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго. Свойство: вертикальные углы равны. Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой. Свойство: сумма смежных углов равна 180 ° . ( 1 ) и ( 3 ) называются вертикальными . По свойству вертикальных углов: ∠ C O D = ∠ A O B ( 1 ) и ( 2 ) называются смежными . По свойству смежных углов: ∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 ° Видео:Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать  Углы, образованные при пересечении двух прямых секущейПрямая, пересекающая две заданные прямые, называется секущей этих прямых. Существует пять видов углов, которые образуются при пересечении двух прямых секущей. ( 1 ) и ( 5 ) называются соответственными . ( 3 ) и ( 5 ) называются внутренними односторонними . ( 1 ) и ( 7 ) называются внешними односторонними . ( 3 ) и ( 6 ) называются внутренними накрест лежащими . ( 1 ) и ( 8 ) называются внешними накрест лежащими . Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:
Видео:Внутренние накрест лежащие углы. Часть 3Скачать  Сумма углов многоугольникаСумма углов произвольного n -угольника вычисляется по формуле: S n = 180 ° ⋅ ( n − 2 ) где n – это количество углов в n -угольнике. Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника. Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 ° Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 ° Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 ° Так можно продолжать до бесконечности. Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны. На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов. α n = 180 ° ⋅ ( n − 2 ) n Видео:Накрест лежащие углыСкачать  Примеры решений заданий из ОГЭМодуль геометрия: задания, связанные с углами 📽️ ВидеоУрок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  Углы внутренние односторонние и внутренние накрест лежащиеСкачать  Внутренние накрест лежащие углы, образованные ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать  ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать  Вписанные углы в окружностиСкачать  №201. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210Скачать  7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  |



































 Если a ∥ b, то
Если a ∥ b, то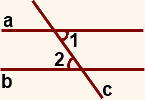 ∠1=∠2.
∠1=∠2.



