Пример №1 . Даны векторы ε1(2;1;3), ε2(3;-2;1), ε3(1;-3;-4), X(7;0;7). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = 2*((-2)*(-4) — (-3)*1) — 3*(1*(-4) — (-3)*3) + 1*(1*1 — (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1α2α3, что имеет место равенство:
X = ⓫ε1 + ⓬ε2 + ⓭ε3
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α1;1α1;3α1😉 + (3α2;-2α2;1α2😉 + (1α3;-3α3;-4α3😉
(7;0;7) = (2α1 + 3α2 + 1α3;1α1 -2α2 -3α3;3α1 + 1α2 -4α3)
По свойству равенства векторов имеем:
2α1 + 3α2 + 1α3 = 7
1α1 -2α2 -3α3 = 0
3α1 + 1α2 -4α3 = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
| X = |
|
X = 2ε1 + ε2
В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
Пример №2 . В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4).
- Онлайн калькулятор. Разложение вектора по базису.
- Калькулятор для разложения вектора по базисным векторам
- Инструкция использования калькулятора для разложение вектора по базисным векторам
- Ввод данных в калькулятор для разложение вектора по базисным векторам
- Дополнительные возможности калькулятора разложение вектора по базисным векторам
- Теория. Разложение вектора по базису
- Координаты вектора в данном базисе.
- 📸 Видео
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Онлайн калькулятор. Разложение вектора по базису.
Этот онлайн калькулятор позволит вам очень просто разложить вектор по базисным векторам.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач и закрепить пройденый материал.
Видео:Координаты в новом базисеСкачать

Калькулятор для разложения вектора по базисным векторам
Выберите размерность пространства
Количество координат в векторе:
Введите значение базисных векторов:
Введите значение вектора, который необходимо разложить по базису:
Инструкция использования калькулятора для разложение вектора по базисным векторам
- Для того чтобы разложить вектор по базисным векторам онлайн:
- выберите необходимую вам размерность пространства (количество координат в векторе);
- введите значения базисных векторов;
- введите значения вектора который нужно разложить по базису;
- Нажмите кнопку «Разложить вектор по базису» и вы получите детальное решение задачи.
Ввод данных в калькулятор для разложение вектора по базисным векторам
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора разложение вектора по базисным векторам
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Видео:Найдите разложение вектора по векторам (базису)Скачать

Теория. Разложение вектора по базису
Чтобы разложить, вектор b по базисным векторам a1 , . an , необходимо найти коэффициенты x 1, . xn , при которых линейная комбинация векторов a1 , . an равна вектору b .
Коэффициенты x 1, . xn будут координатами вектора b в базисе a1 , . an .
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Разложение вектора по базису. 9 класс.Скачать

Координаты вектора в данном базисе.
Дата добавления: 2015-08-06 ; просмотров: 9227 ; Нарушение авторских прав
Базисом векторного пространства называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства можно представить в виде линейной комбинации векторов этой системы.
В трехмерном векторном пространстве базис состоит из трех векторов, который обычно обозначается так: <е1, е2, е3 >.
Базис называется ортонормированным, если длины всех базисных векторов равны единицы, и базисные векторы попарно перпендикулярны. Ортонормированный базис обычно обозначается так: <i, j, k>.
Координатами вектора m в базисе <е1, е2, е3 >называются коэффициенты разложения вектора m по векторам базиса, т.е. если m = хе1 + уе2 + zе3, то числа х, у, z — координаты вектора m. В этом случае будем записывать m(х, у, z).
Имеет место теорема о координатах линейной комбинации:
1.24. Даны векторы а(2, 3, -1), b (0,1,4), с(1,0,-3). Найти координаты векторов: а) 2а — b —2с,б)а — b —3с,в)а +2b +3с),г) а — b – с,
д) 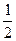

ОТВЕТ. а) (2,5,0), б) (-1,2,4), в) (5,5,-2), г) (1,2,-2), д) (1,1,3), е) (1, 
ПРИМЕР 1.7
Даны векторы а(1,1,2), b (-2, 3 5), с(-4,1,1), d (0, -1, 3) Можно ли вектор dпредставить в виде линейной комбинации векторов а, b, с? Если да, то найти коэффициенты этой линейной комбинации.
Выясним, существуют ли такие числи х, у, z, что
d =ха +уb +z с.(1)
По теореме о координатах линейной комбинации векторов из равенства (1) получаем выражение для первой координаты вектора dчерез первые координаты векторов а, b, с, и аналогичные выражения для вторых и третьих координат
0 = х — 2у — 4 z (2)
Выясним, имеет ли эта система решение. Из (2) следует, что
Затем, подставляя (5) в (3) и (4), получаем:
Система, состоящая из уравнений (2), (3), (4), равносильна системе, состоящей из уравнений (5), (6), (7) . Ясно, что последняя система не имеет решений, следовательно, и данная система не имеет решений,. Поэтому вектор dнельзяпредставить в виде линейной комбинации векторов а, b, с. ■
1.25. Определить, какие из данных троек векторов линейно зависимы:
а) а(-3,0, 2), b (2, 1, -4), с(11, -2, -2); б) а(1, 0, 7), b (-1, 2, 4), с(3, 2, 1);
в) а(5, -1,4),b (3,-5, 2), с(-1,-13, -2).
ОТВЕТ.. а), с) линейно зависимы.
1.26. Представить вектор d как линейную комбинацию векторов а, b, с:
1)а(2,3,1), b (5, 7, 0), с(3, -2, 4), d (4, 12, -3);
2) а(5, -2, 0), b (0, -3, 4), с(-6, 0, 1), d (25, -22, 16);
3)а(3, 5, 6), b (2, -7, 1), с(12, 0, 6), d (0, 20, 18).
ОТВЕТ. 1) d = а + b + с, 2) d = 5а + 4b, 3) d = 4а – с.
1.27. Можно ли вектор d (1,1,1) представить в виде линейной комбинации векторов а(1,-1,0), b (2,2,1), с(0,-4,-1)?
ОТВЕТ.. Нет.
1.28. Даны векторы а(х, 3, 4), b (-1, 5, у).Существуют ли такие числа х и у, для которых система векторов <а, b >линейно зависима ?
ОТВЕТ. Да, х = — 
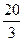
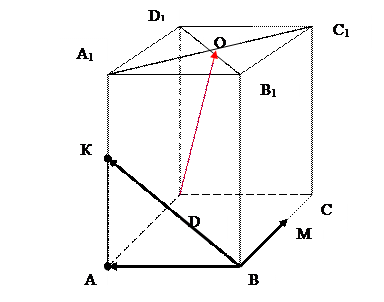
ПРИМЕР 1.8
В параллелепипеде АВСDА1В1С1D1 К – середина ребра АА1, точка М лежит на ребре ВС и ВМ = 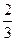
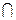

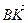

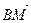
Так как координаты вектора в данном базисе это коэффициенты разложения этого вектора по векторам базиса, то данную задачу можно сформулировать так: выразить вектор 
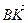

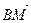
1) 
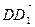
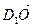
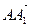
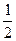
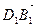
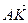
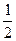
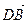

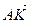
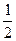
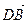
2) Выразим вектор 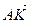
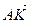
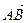
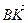

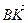
3) Выразим вектор 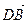
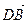
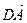
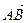
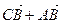
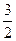
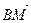

4) Подставим (2) и (3) в (1), получим


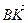
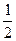
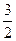
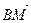

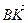

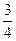
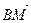
Следовательно, первая координата вектора 
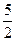
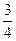

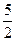
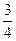
ОТВЕТ. 
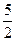
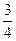
1.29. АВСD – тетраэдр. М и К – точки пересечения медиан граней ВСD и АDС, N – середина АВ, Р 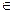
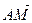
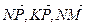
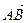
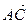
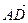
ОТВЕТ. 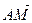



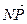
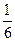

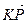
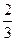

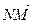
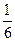


1.30. АВСD – тетраэдр. N и К середины ребер ВС и АС. Найти координаты векторов 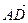
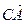
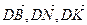
ОТВЕТ. 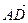
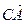
1.31. В тетраэдре АВСD М- середина ВС, а N – точка пересечения медиан грани АDС. Найти координаты векторов 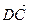
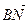
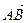
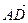
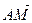
ОТВЕТ. 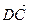
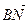
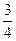

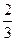
1.32. В тетраэдре АВСD N — середина ВС, а М и К – точки пересечения медиан граней ВСD и АВD. Найти координаты векторов 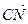
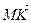
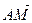
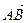
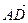
ОТВЕТ. 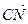
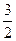
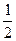


📸 Видео
Координаты вектора. 9 класс.Скачать

Координаты точки и координаты вектора 1.Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Базис. Разложение вектора по базису.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Образуют ли данные векторы базисСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Координаты вектора в базисе. Собственные числа и векторы (решение задач)Скачать

Координаты вектора в пространстве. 11 класс.Скачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Семинар №4 "Замена базиса и системы координат"Скачать

Замена базиса. ТемаСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать