Вектор умова для плоской волны

ЛЕКЦИЯ №2

МЕХАНИЧЕСКИЕ ВОЛНЫ. АКУСТИКА

ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В широком смысле, под волной понимают процесс распространения в пространстве колебаний или возмущений состояния вещества или поля с течением времени. Математически этот процесс выражается функцией, описывающей распространение в пространстве изменений какой-либо физической величины. Выделяют три типа волн: волны на поверхности жидкости, упругие (иначе механические) и электромагнитные. Рассмотрим механические волны, т.е. процессы распространения механических возмущений в упругой среде.

Механические колебания, возбужденные в какой-либо точке пространства вследствие взаимодействия между упруго связанными частицами среды будут распространяться в ней с некоторой конечной скоростью. Частицы среды последовательно вовлекаются в колебательное движение около своих положений равновесия, но не перемещаются вместе с волной. Таким образом, в волновом процессе не происходит переноса массы. От частицы к частице передается только колебательное движение, а значит, и энергия.Перенос энергии без переноса вещества – это основное свойство всех волн, независимо от их природы.

Волны бывают продольные, если колебания частиц среды происходят вдоль направления распространения, и поперечные, если направление колебаний перпендикулярно вектору скорости волны. Очевидно, что в случае продольных волн в среде возникают деформации сжатия и разрежения, которые в свою очередь приводят к образованию локальных областей сгущения и разрежения вещества, т.е. области повышенного и пониженного давления. Такие волны могут возникать в любых средах: в газах, жидкостях и твердых телах. Поперечные механические волны обусловлены деформациями сдвига. Это означает, что они могут существовать только в твердых телах.

В общем случае, волны представляют собой пространственное образование. Геометрическое место точек (поверхность), до которых колебания дошли к некоторому моменту времени, называется фронтом волны. В зависимости от формы фронта волны бывают: плоские, сферические, цилиндрические и т.д.

Поверхность, точки которой имеют одно и то же значение фазы, называется волновой поверхностью. Волновых поверхностей

бесчисленное множество, а фронт волны всегда один.

УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ

Получим уравнение плоской волны в однородной среде вдоль оси 0х, совпадающей с направлением её распространения. Т.к., в этом случае фронт волны перпендикулярен 0х, то смещения s частиц среды будут зависеть только от координаты х и момента времени t, т.е. уравнение волны будет представлять собой функцию – s = f(x,t). Пред-положим, что в точке 0 (рис.1) частица совершает колебания по гармоническому закону: s = Acosωt. Тогда, очевидно, что колебания в некоторой точке М, удаленной от точки 0 на расстояние 0М = х, будут совершаться по тому же закону, но с некоторым отставанием по времени τ от колебаний в точке 0:

Если обозначить скорость волны через u, то время запаздывания, за которое волна добежит от точки 0 до точки М: τ = х/u, и уравнение колебаний в произвольной точке М на расстоянии х от источника примет вид:

s= A cos ω( t-τ ) = A cos ω( t — ). (2)

Это и есть искомое уравнение плоской бегущей волны. Здесь: А – амплитуда смещения частиц среды от положения равновесия, ω – циклическая частота колебаний частиц, ω( t — ) – фаза колебаний в точке с координатой х, u – скорость плоской волны.

Расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе, называется длиной волны λ (рис.1).

Длина волны равна расстоянию, на которое распространяется определенная фаза колебаний за период колебаний частиц среды. Тогда λ = u·T = u/ν. Т.к. ω = 2πν, то (2) можно переписать в виде:

s = Acosω( t — ) = Acos2π(vt — ) = Acos(ωt — 2π ). (3)

Покажем, что скорость распространения волны u – это скорость перемещения фиксированного значения фазы. Положим ω( t – ) = С, т.е. const. Выразим х: х = ut — Cu/ω. Продифференцировав это выражение по t, получим: (С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью.

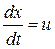
Скорость распространения механических волн зависит от физических свойств среды. Скорость распространения продольных волн определяется формулой: . Для поперечных волн – . Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.

Основные свойства волн: прямолинейность распространения в однородной среде, отражение и преломление на границе раздела сред, дисперсия, интерференция и дифракция.

ВОЛНОВОЕ УРАВНЕНИЕ

Аналогично тому, как уравнение колебаний является решением дифференциального уравнения, описывающего процесс колебаний, так и уравнение волны представляет собой решение дифференциального уравнения, описывающего процесс распространения волн в среде. Это дифференциальное уравнение второго порядка в частных производных называется волновым. Найдем его вид. Запишем первые и вторые производные уравнения волны (2) по переменным t и х:

; ;

; ; (4)

; . (5)

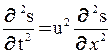
В трехмерном случае:

.

СТОЯЧИЕ ВОЛНЫ

Рассмотрим в качестве примера проявления волновых свойств механизм образования стоячих волн. Они возникают в результате наложения (интерференции) двух встречных плоских когерентных волн с одинаковой амплитудой. Например, волны падающей и этой же волны отраженной от границы раздела сред. Запишем уравнения двух плоских волн, движущихся навстречу друг другу в виде (3).

s ₁= Acos(ωt – 2π ) = А(cosωt cos2π + sinωt sin2π ) . (6)

s₂ = Acos(ωt + 2π ) = А(cosωt cos2π – sinωt sin2π ). (7)

Складывая эти равенства, получим уравнение результирующего процесса – уравнение стоячей волны:

(8)

Из (8) видно, что в каждой точке среды происходит колебание той же частоты ω, что и у интерферирующих волн. Однако амплитуда колебаний каждой частицы зависит от координаты точки среды, в которой она расположена: А_х = 2А cos2π . В точках, где аргумент 2π = ±nπ (при n = 0, 1, 2…) и |cos2π | = 1, амплитуда имеет максимальное значение –2А. Эти точки называются пучностями стоячей волны. В точках, где аргумент 2π = ±(n + )π, амплитуда минимальна и равна нулю, т.к. в этом случае cos2π = 0. Эти точки называются узлами стоячей волны.

На рис.2 показано как меняется расположение частиц среды в стоячей волне в течение периода.

ЭНЕРГИЯ ВОЛНЫ. ВЕКТОР УМОВА

Последовательное вовлечение в колебательное движение частиц среды означает, что волна передает от частицы к частице некоторую механическую энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Найдем выражение для энергии, переносимой плоской волной. Для этого рассмотрим некоторый объем V среды, все частицы которой вовлечены волной в колебательное движение (рис.3). В момент времени t каждая частица массой m₀ имеет определенные значения смещения и скорости. Однако, как мы установили ранее, полная механическая энергия частицы от этого не зависит и равна Е_м = , где m₀ – масса одной частицы. Полагая, что все частицы среды одинаковы, а их число в объеме V равно N, получим для энергии этого объема:

, (9)

где m = m₀·N масса вещества в объеме V. Разделив правую и левую часть этого равенства на V , получим количество энергии в единице объема волны. Эта величина называется объемной плотностью энергии:

, (10)

где ρ = m / V – плотность вещества среды, в которой распространяется волна. Объемная плотность энергии измеряется в Дж / м 3 .

Определим энергию, переносимую волной через площадку площадью S перпендикулярную 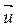(рис.3). За время t волна удалится от S на расстояние Δl = u·t и вовлечет в колебательное движение частицы в объеме V = S·u·t, перенеся при этом через площадку S энергию W = w∙V = w∙S∙ut.

Количество энергии, перенесенное через площадку S за единицу времени называется потоком энергии волны:

Ф = = w∙ S∙u. (11)

Поток энергии измеряется в Дж / с = Вт.

Количество энергии переносимое через единицу площади за единицу времени называется интенсивностью (или плотностью потока) энергии волны и измеряется в Вт / м 2 или Дж / (с·м 2 ):

. (12)

Т.к. скорость величина векторная, а w скалярная, то справа в этом равенстве стоит вектор. Это означает, что и левая величина дол-жна быть векторной, т.е. интенсивность энергии волны в направлении переноса – это некий вектор:

. (13)

Эта величина для упругих волн называется вектором Умова, который определяет количество энергии переносимое механической волной через единицу площади за единицу времени в направлении .

ЭФФЕКТ ДОПЛЕРА

Эффектом Доплера называют изменение частоты колебаний, воспринимаемых наблюдателем (приёмником волны) вследствие движения источника волны и наблюдателя относительно среды.

Рассмотрим простейший случай, когда источник волны и наблюдатель движутся вдоль соединяющей их прямой. Скорость распространения волны в рассматриваемой среде будем считать равной u, скорость источника – , скорость наблюдателя (приёмника) – , частота колебаний источника – ν_0, период колебаний источника – Т = 1/ ν₀. Все скорости определены относительно среды. Скорость источника будем считать положительной, если он движется по направлению к приёмнику, и отрицательной, если источник удаляется от приёмника. Аналогичное правило знаков скоростей примем и для приёмника.

В исходном состоянии источник находится в начале координат (точка 0), а приёмник в точке А. Скорость распространения колебаний зависит только от свойств среды, поэтому при неподвижном источнике за одну секунду волна пройдет в направлении к приемнику расстояние u. На этом расстоянии уложится ν₀ колебаний. Соответственно, длина волны – λ₀ = u / ν₀ (рис.4а).

Пусть наблюдатель неподвижен и находится на расстоянии u от источника, а источник волны движется с постоянной скоростью по направлению к наблюдателю. Будем считать, что

Видео:Вектор Умова-Пойнтинга ● 2Скачать

Вектор Умова-Пойнтинга

Вы будете перенаправлены на Автор24

Вектор потока электромагнитной энергии, определяемый как:

называют вектором Умова — Пойнтинга (вектором Пойнтинга). Понятие вектора как потока энергии в разных веществах было введено Н.А. Умовым, а математическое выражение (1) получено Пойнтингом.

В электромагнитной волне векторы $overrightarrow и overrightarrow$ перпендикулярны, следовательно, модуль вектора $overrightarrow

$ имеет выражение:

Направление вектора Умова — Пойнтинга перпендикулярно к векторам $overrightarrowи overrightarrow$, и со направленно с направлением распространения волны ($overrightarrow$).

Для плоской электромагнитной волны выражение для модуля вектора Умова — Пойнтинга имеет вид:

и между мгновенными значениями напряженности магнитного и электрического полей в электромагнитной волне существует соотношение:

Модуль вектора Умова — Пойнтинга можно выразить как:

В диэлектрике объемная плотность электромагнитного поля равна:

Следовательно, сравнивая равенства (6) и (7), имеем:

В уравнения (2) -(8) входят мгновенные значения величин. Векторы в световой волне совершают колебания с частотами около $^Гц$, следовательно, весьма затруднительно следить за изменением величин во времени. Поэтому обращаются к средним значениям, переходя от мгновенных величин. Если электромагнитная волна является плоской, то среднее значение по времени вектора Умова — Пойнтинга равно:

Вектор Умова — Пойнтинга связан с энергией, которую несет электромагнитная волна соотношением:

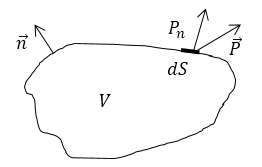
где $frac$ — энергия, проходящая через площадку $S$ в единицу времени, $P_n=Pcosalpha $ — проекция вектора $overrightarrow

$ на нормаль $overrightarrow$ к площадке $S$. Направление вектора Умова — Пойнтинга дает характеристику движения энергии в электромагнитном поле.

Готовые работы на аналогичную тему

Если представить линии, касательные к которым в каждой точке совпадают с направлениями вектора $overrightarrow

$, то такие линии есть пути распространения энергии электромагнитного поля. В оптике подобные линии называют лучами.

Видео:Вектор Умова-Пойнтинга ● 1Скачать

Теорема Пойнтинга

Для теории электромагнитных полей формулировки законов сохранения энергии и импульса имеет весьма важное значение. Теорема Пойнтинга — один из видов формулировок закона сохранения энергии: Скорость возрастания электромагнитной энергии внутри некоторого объема в сумме с энергией, которая вытекает за единицу времени через поверхность, ограничивающую тот же объем, равна полной работе, которую совершает поле над источниками внутри заданного объема, если взять ее со знаком минус.

Поясним данную формулировку. Выделим внутри некоторой среды объем $V$, который ограничивает поверхность $S$ (рис.1). Допустим, что полная энергия, которая заключена внутри объема, равна $W$. Тогда можно записать:

где $P_n$ — нормальная составляющая вектора Умова — Пойнтинга. Интегрирование в (4) производят по всей замкнутой поверхности $S$. Положительным считают направление внешней нормали $overrightarrow$, что означает поток вектора $overrightarrow

$ (выражение, которое стоит в формуле (4) в правой части) считают большим нуля, если линии потока энергии $overrightarrow

$ выводят наружу из объема.

При этом $-frac$- величина, на которую уменьшатся, полная энергия внутри объема $V$ за единицу времени. По закону сохранения энергии она должна быть равна энергии, которая выходит через поверхность $S$ за единицу времени наружу. Следовательно, энергия, покидающая объем $V$ через поверхность $S$, выражена потоком вектора Умова — Пойнтинга.

Задание: Напишите выражение для вектора Умова — Пойнтинга, если энергию переносит волна, уравнение изменения вектора напряженности электрического поля которой задано как: $overrightarrow=10cosleft(omega t-kx+alpha right)overrightarrow(frac).$ Учесть, что амплитуда вектора напряженности магнитного поля имеет вид: $H_moverrightarrow$, частота волны $omega при ней varepsilon =2, mu approx 1 .$

Решение:

За основу решения задачи, примем определение вектора Умова — Пойнтинга:

Из условий видим, что колебания вектора напряженности электрического поля происходят по $оси Z$, колебания вектора напряженности магнитного поля по $оси X$, следовательно, вектор Умова — Пойнтинга колеблется по $оси Y$.

Модуль искомого вектора можно найти как:

Найдем амплитуду вектора $overrightarrow$, если знаем, что амплитудные значения в нашем случае связаны соотношением:

Выразим из (1.3) искомую амплитуду $H_m$, имеем:

При этом уравнение колебаний вектора напряженности запишем в виде:

Используя уравнения (1.1), (1.5) и уравнение колебаний вектора напряжённости электрического поля из условий задачи, запишем выражение для вектора Умова — Пойнтинга:

Ответ: $overrightarrow

=sqrt<frac<varepsilon _0><mu _0>>^2c^2left(omega t-kx+alpha right)overrightarrow.$

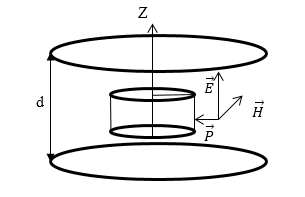
Задание: Плоский конденсатор, имеющий круглые обкладки заряжен постоянным током за время $t_0$ до напряжения $U$. Расстояние между пластинами конденсатора равно $d$. Запишите выражение для вектора Умова — Пойнтинга для точек воображаемой цилиндрической поверхности радиуса $r$, которая находится между обкладками конденсатора. Считайте, что радиус пластин конденсатора много больше, чем радиус воображаемого цилиндра.

Решение:

За основу решения задачи, примем определение вектора Умова — Пойнтинга:

Переменное электрическое поле, возникающее в результате разрядки конденсатора, вызывает переменное магнитное поле. Запишем уравнение из системы Максвелла, учитывая, что между обкладками конденсатора токов проводимости нет:

и материальное уравнение:

Возьмем производную от $overrightarrow$ по времени:

Возьмём интеграл от $rotoverrightarrow$ по поверхности цилиндра радиуса $r$, применим теорему Стокса:

Приравняем правые части выражений (2.6), (2.7), согласно тому, что выполняется (2.5):

Найдем модуль вектора Умова — Пойнтинга согласно выражениям (2.1) и (2.8):

Задание: Плоская электромагнитная волна распространяется в вакууме по $оси X$. Чему равна средняя энергия, которая проходит через единицу поверхности в единицу времени?

Решение:

сли мы имеем плоскую электромагнитную волну, то модули напряженности полей $overrightarrow $и $overrightarrow$ в произвольной точке $x$ могут быть выражены как:

где $k=frac$. Следовательно, мгновенное значение вектора $overrightarrow

$ можно записать в виде:

[P=E_0<H_0^2 left(omega t-kxright) >left(1.3right).]

По условию задачи волна распространяется в вакууме, следовательно, $varepsilon =1, mu =1 $, имеем следующее соотношение между амплитудами полей:

Кроме того, известно, что среднее значение $leftlangle ^2alpha rightrangle =frac,$ тогда используем (1.3), (1.4) получаем среднее значение вектора Умова — Пойнтинга ($leftlangle Prightrangle $) равно:

Ответ: Средняя энергия, которая проходит через единицу поверхности за единицу времени (интенсивность волны), равна $leftlangle Prightrangle =sqrt<frac<_0><_0>>frac.$

Задание: Вычислите среднее значение вектора Умова — Пойнтинга в стоячей волне.

Решение:

Колебания электрического и магнитного полей можно представить в стоячей волне с использованием следующих гармонических законов:

где $_E, varphi_H$- запаздывание по фазе отраженной волны соответствующего поля, то есть:

здесь $theta ,vartheta $ — изменение фазы при отражении, они равны или $pi , $или 0. $l-$длина линии (если рассматривается свободная волна, то это расстояние от излучателя до поверхности отражения). Обозначим:

тогда колебания, исходя из (2.1) и (2.2) в точке $x$ можно записать как:

при этом очевидно, что $E_1$ и $H_1$ не зависят от времени. Допустим, что $theta =pi $, тогда:

Исходя из (2.9) и (2.10), для вектора Умова — Пойнтинга получим:

Из формулы (2.11) следует, что колебания модуля вектора $overrightarrow

$ происходят с частотой $2omega $, при этом периодически изменяется знак. Следовательно, среднее значение вектора по времени равно $0$ ($leftlangle Prightrangle =0$).

Ответ: В стоячей волне течения энергии нет, $leftlangle Prightrangle =0$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 02 2022

Видео:Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать

Вектор Пойнтинга (вектор Умова — Пойнтинга)

Перенос энергии бегущей упругой и электромагнитной волной определяют при помощи вектора, который называют вектором потока энергии. Этот вектор обозначим как $overline $(встречается обозначение $overline

$) Он показывает количество энергии, протекающее в волне за единицу времени через единицу площади поперечного сечения волны. Для электромагнитных волн данный вектор был введен Пойнтингом в 1884 г. Скорость переноса энергии при помощи вектора Пойнтинга не изменяется и равна характеристической скорости распространения электромагнитной волны в пространстве. Сейчас данный вектор ($overline$) называют вектором Умова — Пойнтинга.

Видео:Билеты № 35, 39 "Плоская волна, ее отражение. Давление излучения"Скачать

Определение

Вектором Умова — Пойнтинга ($overline$) называют физическую величину, определяющую поток энергии электромагнитного поля, который равен:

где $overline$ — напряженность электрического поля; $overline$ — напряженность магнитного поля. Направлен $overline$ перпендикулярно $overline$ и $overline$ и совпадает с направлением распространения электромагнитной волны.

Видео:Электромагнитные волны. Поток энергии. Вектор Умова-Пойтинга.Скачать

Величина вектора Умова — Пойнтинга

Правая часть формулы (1) представляет собой векторное произведение векторов, значит, величина вектора Умова — Пойнтинга для электромагнитной волны равна:

где $alpha $ — угол между векторами $overline$ и $overline$, но $overlinebot $ $overline$, следовательно, получаем для электромагнитной волны:

Вектор $overline $удовлетворяет в свободном пространстве уравнению непрерывности:

где $w$ — объемная плотность энергии электромагнитного поля.

Видео:Билет №38 "Поток энергии"Скачать

Вектор Умова — Пойнтинга плоской электромагнитной волны

В случае плоской электромагнитной волны величина вектора $overline$ равна:

где $u$ $=frac<sqrt<_0mu varepsilon _0>>$- фазовая скорость распространения электромагнитного возмущения в веществе с диэлектрической проницаемостью $varepsilon $ и магнитной проницаемостью $mu .$

где $c$ — скорость света в вакууме.

Мгновенные величины напряженности магнитного и электрического полей в рассматриваемой волне связаны соотношением:

выразим напряженность $H$:

Учитывая формулу (8) величину вектора $overline$ запишем как:

В изотропном веществе объемную плотность энергии электромагнитного поля найдем как:

Учитывая формулы (6) и (10) запишем еще одно выражение для величины вектора $overline$:

На практике переходят от мгновенных величин к их средним значениям. Для плоской электромагнитной волны средняя величина по времени вектора Умова — Пойнтинга равна:

Модуль величины $left|_tright|$ называют интенсивностью ($I$) электромагнитной волны:

Направление вектора Умова — Пойнтинга показывает направление движения энергии в электромагнитном поле. Если изобразить линии, касательные к которым в любой точке совпадут с направлениями вектора $overline$, то такие линии будут являться путями распространения энергии электромагнитного поля. В оптике это лучи.

Видео:Вектор Умова-Пойнтинга ● 3Скачать

Примеры задач с решением

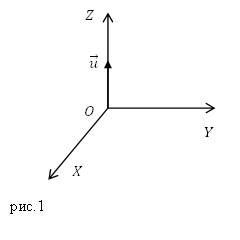
Задание. На рис.1 изображен вектор фазовой скорости плоской электромагнитной волны. В какой плоскости расположены векторы $overline$ и $overline$ полей этой волны?

Решение. Основой решения нашей задачи будем считать определение вектора $overline$:

Вектор $overline$ является результатом векторного произведения векторов$overline$ и $overline$, он направлен в сторону распространения электромагнитной волны, следовательно, $overlineuparrow uparrow overline$, для рис.1 вектор Умова — Пойнтинга направлен по оси Z. Значит, векторы $overlineи overline$ лежат в плоскости XOY.

Ответ. XOY

Задание. Запишите модуль среднего вектора Умова — Пойнтинга электромагнитной волны: $overline=E_0 $Считайте, что волна распространяется в вакууме по оси X.

Решение. Модуль вектора Умова — Пойнтинга для электромагнитной волны:

где $E$ и $H$ — мгновенные значения электрического и магнитного полей. Мгновенное значение вектора Умова — Пойнтинга будет равно:

[S=EH=E_0H_0<^2 left(omega t-kxright)(2.2), >]

где $H_0$ — амплитуда колебаний напряженности магнитного поля.

Средняя величина $_t$ может быть найдена:

принимая во внимание, что $<leftlangle <^2 left(omega t-kxright) >rightrangle >_t=frac$, для вакуума имеем:

🎬 Видео

Лекция 2 ВолныСкачать

Механические модели волн. 1.Скачать

Вектор Умова-Пойнтинга ● 5Скачать

Получение уравнения плоской бегущей волны.Скачать

Билет №34 "Электромагнитные волны"Скачать

Колебания и волны. Лекция 16. Вектор Умова - ПоинтингаСкачать

4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать

Энергия течёт в пространстве а не в проводе Вектор Умова ПойтингаСкачать

Урок 370. Механические волны. Математическое описание бегущей волныСкачать

4.8 Плотность потока мощности электромагнитной волныСкачать

Средняя плотность потока энергии. вектор Пойнтинга.Скачать