1. Свойство углов, образованных при пересечении двух параллельных прямых третьей прямой (формулировки и примеры)
При пересечении двух прямых секущей, образуется 8 уг-
лов. На рисунке 8 обозначим их цифрами.
Углы 3 и 5, 4 и 6 — накрест лежащие;
Углы 4 и 5, 3 и 6 — односторонние;
Углы 1 и 5, 4 и 8, 2 и 6, 3 и 7 — соответственные.
Если прямые а и Ь на рис.8 параллельны, то эти углы
имеют специальные свойства:
Теорема: Если две параллельные прямые пересечены се-
кущей, то накрест лежащие углы равны.
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
2. Решение треугольника по двум сторонам и углу между ними.
Решением треугольника называется нахождение всех его шести элементов (трех сторон и трех углов) по каким-нибудь трем заданным элементам, определяющим треугольник.
Решение треугольника по двум сторонам и углу между ними
То есть мы нашли три неизвестных элемента треугольника, а значит, решили треугольник.
3. Задача по теме »Средняя линия треугольника» (типа №46-48)
№46. В треугольнике ABC отмечены точки D и E, которые являются серединами сторон AB и BC соответственно Найдите периметр четырехугольника ADEC, если AB=24 см, BC=32 см и АС=44 см
DE — средняя линия треугольника ABC по определению. По свойству средней линии (средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьем стороне и равна ее половине)
Периметр четырехугольника ADEC равен
№ 47 . Диагональ квадрата равна 26 см. Найдите периметр
четырехугольника, вершинами которого являются середи-
ны сторон квадрата.
Периметр четырехугольника EFGH равен EF+FG+GH+HE=4EF=4*13=52 cм.
№ 48 . В равностороннем треугольнике QRP отмечены точки S, T и O, которые являются серединами сторон QR, RP и QP соответственно. Найдите периметр параллелограмма QSTO, если периметр треугольника SRT равен 27 см.
ST — средняя линия треугольника QRP, по свойству средней линии она параллельна QP и равна . Треугольники следовательно, т. SPT — равносторонний , и SR=RT=ST, его периметр равен SR+RT+ST= 27 см, откуда получаем, что 3SR=27 cм; SR=9см=RT=ST. QO= = ST=9 см; QS= =SR=9 см. В параллелограмме противоположные стороны равны, значит, SQ=TO. Следовательно, периметр параллелограмма QSTO равен ST+TO+OQ+QS=36см.
4. Задача по теме «Неравенство треугольника»
(типа № 44)
№ 44. Расстояние от точки А до точек В и С равны 3 см и
14 см соответственно, а расстояния от точки D до точек
В и С равны 5 см и б см соответственно. Докажите, что
точки А, В, С и D лежат на одной прямой.
AC=14, AB=3, CD=6, BD=5 (см)
Проведем отрезок AC. Проведем окружность с центром в точке A радиуса 3 см. Точка B лежит на этой окружности. При этом AM=3 cм. Проведем окружность с центром в точке С радиуса 6 см. Точка D лежит на этой окружности. При этом CN=6 см. Тогда MN=AC-AM-CN=5 см. Теперь видим, что BD=5см, тогда и только тогда, когда точки B и D лежат на отрезке AC. Что и требовалось доказать.
Признаки параллельности прямых
При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.
Углы, образующиеся при пересечении двух прямых третьей прямой
| Рисунок | Определение углов |
 | Внутренние накрест лежащие углы |
 | |
 | Внешние накрест лежащие углы |
 | |
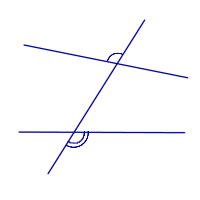 | Соответственные углы |
 | |
 | |
 | |
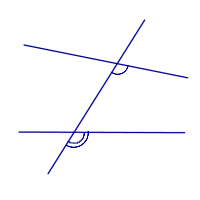 | Внутренние односторонние углы |
 | |
 | Внешние односторонние углы |
 |
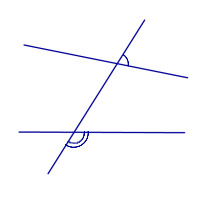| Внутренние накрест лежащие углы |
|
|
| Внешние накрест лежащие углы |
|
|
| Соответственные углы |
|
|
|
|
| Внутренние односторонние углы |
|
|
| Внешние односторонние углы |
|
|
Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.
Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.
Признаки параллельности двух прямых
| Рисунок | Признак параллельности |
 | Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны |
 | |
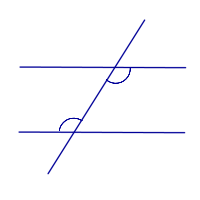 | Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны |
 | |
 | Прямые параллельны тогда и только тогда, когда соответственные углы равны |
 | |
 | |
 | |
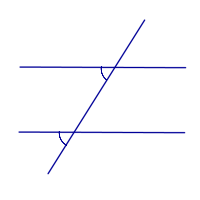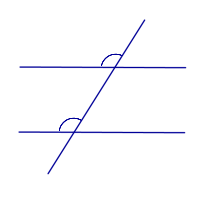 | Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180° |
 | |
 | Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180° |
 |
Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны
Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны
Прямые параллельны тогда и только тогда,
когда соответственные углы равны
Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°
Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°
| Рисунок | Признак параллельности |
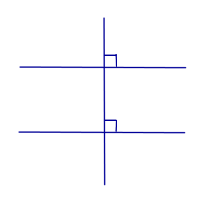 | Две прямые, перпендикулярные к третьей прямой, параллельны |
Две прямые, перпендикулярные к третьей прямой, параллельны
Переход свойства параллельности прямых
| Рисунок | Признак параллельности |
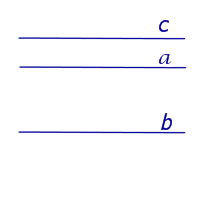 | Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c |
Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c
Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.
Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.
Углы при пересечении двух прямых
Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.
На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).
Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:
| Соответственные углы: ∠1 и ∠5, ∠3 и ∠7, ∠2 и ∠6, ∠4 и ∠8. |  |
| Внутренние накрест лежащие углы: ∠3 и ∠6, ∠4 и ∠5. |  |
| Внешние накрест лежащие углы: ∠1 и ∠8, ∠2 и ∠7. |  |
| Внутренние односторонние углы: ∠3 и ∠5, ∠4 и ∠6. |  |
| Внешние односторонние углы: ∠1 и ∠7, ∠2 и ∠8. |  |
Углы при пересечении параллельных прямых
Если секущая пересекает две параллельные прямые линии, то:
- внутренние накрест лежащие углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответственные углы равны;
- внешние накрест лежащие углы равны;
- сумма внешних односторонних углов равна 180°.