Вектор и векторная величина

Содержание:

Физические величины служат для численного выражения различных характеристик материальных предметов и физических явлений. Все физические величины разделены на два вида. Векторные величины в физике – это те, которые кроме численного выражения обязательно характеризуются направлением. А вот обычные величины называют скалярными. Примерами таких величин могут служить:

• температура;
• яркость;
• энергия;
• поглощенная доза радиации;
• мощность.

Видео:Скалярные и векторные величины, основные определения.Скачать

Что такое векторная величина

Векторные величины в физике, список которых приведен ниже, широко известны:

• сила;
• ускорение;
• скорость;
• магнитная индукция;
• импульс;
• напряженность магнитного поля.

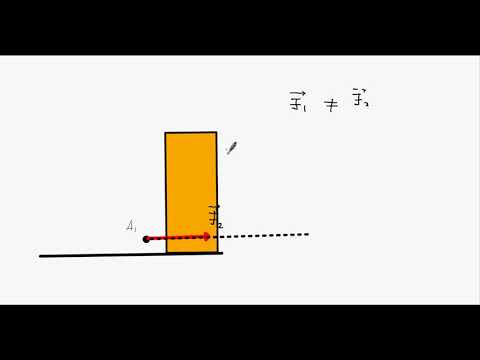
Чтобы досконально разобраться в их смысле, попробуем рассмотреть простой пример. Каждый из нас неоднократно бросал или подбрасывал какой-либо предмет. Пусть это будет теннисный мячик. Сделать это можно разными способами:

• подбросить вертикально вверх;
• бросить параллельно поверхности земли, то есть горизонтально;
• метнуть под углом к горизонту.

В нашем эксперименте будем предполагать, что все три раза мячик бросает один и тот же человек, а сила броска всегда примерно одинакова. Какие результаты будут в итоге? Догадаться довольно просто: в каждом из случаев результат будет разным, потому что три раза мячик бросали в разном направлении. Таким образом мы увидели, что векторная величина это в физике одновременно две характеристики какого-либо физического процесса или состояния.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Действия над векторными величинами

Теперь, когда мы установили, что такое векторная величина в физике, настало время подумать о действиях над такими величинами. Их можно складывать, вычитать, умножать, но важно помнить, что определяющим фактором будет их направление. Действия над такими величинами производят с использованием правил, принятых в математике. Например, сложение векторов производят с использованием правил треугольника или параллелограмма.

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Что значит векторная величина в обычной жизни

В повседневной жизни мы зачастую даже не задумываемся, что значит векторная величина, и не замечем, что пользуемся векторами. Допустим, что два друга собрались поехать на рыбалку и договорились о встрече с утра за 100 м от автобусной остановки. Согласитесь, что намеченное мероприятие может оказаться под угрозой из-за того, что не было указано в каком конкретно направлении от остановки следует двигаться на указанное расстояние.

Другой пример из всем известной басни. Речь про лебедя, рака и щуку, которые дружно собрались потянуть тяжелый воз. Тяговую силу каждый из них приложил в своем направлении, не согласовав его с другими. В итоге воз не тронулся с места. Говоря языком физики, все векторные величины силы математически сложились так, что их равнодействующая оказалась равной нулю.

Ну и в заключительной части вспомним о том, что векторы в виде указующих стрелок принято использовать на дорожных знаках и различных табличках, информирующих о направлении движения в непредвиденных ситуациях либо помогающих найти соответствующий объект.

Видео:Основы кинематики. Тема 2. Скалярные и векторные величины. Действия над векторамиСкачать

Большая теория по векторам

И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь ((L)).

А некоторые имеют и число, и направление — например, перемещение ((vec)).

И сейчас ты узнаешь, почему это настолько важно.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Векторы — коротко о главном

Решать задачи с векторами — легко!

Видео:Физика. Объяснение темы "Векторные и скалярные величины"Скачать

Векторы и… Колумб

В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.

Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.

Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?

Видео:Физика | Ликбез по векторамСкачать

О направлении

Направление – одна из важнейших характеристик движения.

Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.

Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.

Так вот, «просто числа» — это скалярные величины (их также называют скалярами).

А «числа с направлением» — это векторные величины (их иногда называют векторы).

В физике существует множество скалярных и векторных величин.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Что такое скалярная величина?

Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)

Это, например, время, длина, масса, температура (продолжи сам!)

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Что такое векторная величина?

Векторная величина – это величина, которая определяется и значением, и направлением.

В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.

Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):

Видео:Скалярное произведение векторов. 9 класс.Скачать

Как обозначаются векторы?

Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: (vec)

Значение вектора – это модуль вектора, то есть его длина.

Обозначить это можно двумя способами: (left| <vec> right|) или (S)

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Операции над векторами

Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.

Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!

Умножение вектора на число

Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.

(Если направление противоположно, обозначаем так: (vecuparrow downarrow vec))

Рассмотрим на примере, используя клетку для точности построений:

Если вектор умножить на ноль, он станет нулевым.

Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:

Рассмотрим некоторые свойства нулевого вектора.

Если он нулевой, то его длина равна нулю! Логично, не правда ли?

А это значит, что его начало совпадает с концом, это просто какая-то точка.

Нулевой вектор – вектор, начало которого совпадает с концом.

Нулевой вектор принято считать сонаправленным любому вектору.

Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:

А если к любому вектору прибавит нулевой, ничего не изменится:

Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.

Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.

Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.

Две прямые параллельны: (qparallel p)

Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:

Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:

Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:

(vecuparrow downarrow vec)

Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.

Параллельный перенос векторов

Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.

Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство – параллельный перенос.

Сложение векторов по правилу треугольника

Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:

Наша цель – найти такой вектор, который будет являться суммой двух данных:

Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:

Теперь достроим до треугольника.

Но как узнать направление нужного нам вектора?

Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:

Это называется правилом треугольника.

Больше двух слагаемых векторов. Сложение по правилу многоугольника

Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?

Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:

Это называется правилом многоугольника.

Вычитание векторов через сложение

Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:

Тогда нам лишь остается найти сумму с обратным вектором:

А сделать это очень легко по правилу треугольника:

Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.

Вычитание векторов через треугольник

Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.

Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:

Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.

Универсальное правило параллелограмма

Есть еще один способ сложения и вычитания векторов.

Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.

Ничего не напоминает?

Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.

В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:

Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:

Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.

Скалярное произведение векторов

Еще одной важной операцией является произведение векторов. Рассмотрим скалярное произведение. Его результатом является скаляр.

Уравнение очень простое: произведение длин этих векторов на косинус угла между ними.

Векторное произведение векторов

Векторное произведение векторов пригодится нам в электродинамике.

Его формула лишь немного отличается от предыдущей:

В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!

После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:

Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.

Об этом мы поговорим подробнее, когда будем изучать электродинамику.

Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.

Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.

Видео:Векторные величины Сложение векторовСкачать

Проекции векторов

Что такое проекция вектора и с чем ее едят?

Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.

Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.

Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.

Проекция вектора – словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.

Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.

Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.

Именно поэтому необходимо научиться работать с проекциями и осями.

Построение проекции. Определение знака

Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.

Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х₀) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.

Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, – большое заблуждение.

Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:

Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.

В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:

Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:

Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:

Рассмотрим еще один интересный случай.

Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!

Анализ углов

Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!

Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось. Получим угол между вектором и осью.

Если угол острый, проекция положительна:

Если угол тупой, проекция отрицательна:

Обрати особое внимание на то, какой именно угол является углом между вектором и осью!

Частные случаи проекции

Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.

Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180 О ). Это зависит от направления.

При этом длина проекции совпадает с длиной вектора! Смотри!

Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:

Если вектор направлен в другую сторону, проекция отрицательна:

Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.

Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.

Что? Почему раньше не сказал? А… Ну…

Хватит вопросов! Вот тебе пример:

(vec) направлен противоположно оси. Его проекция отрицательна.

Еще один частный случай – работа с обратными векторами.

Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:

Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.

Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.

Прямоугольные треугольники равны по углу и гипотенузе. Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:

Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:

Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.

Проекции обратных векторов равны по модулю и противоположны по знаку.

Давайте еще раз уточним.

Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).

Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.

Проекция вектора бывает отрицательной. Это зависит от направления вектора.

Способы нахождения проекций и векторов с помощью тригонометрии

Зная угол между вектором и осью, можно не прибегать к координатам. Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.

Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.

Рассмотрим вектор и его проекции на оси:

Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:

Тогда обозначим прямой угол и угол между вектором и осью:

Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.

Из этих уравнений легко выражаются проекции.

А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:

Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Действия над проекциями векторов. Решение задач

Умение применять свои знания на практике невероятно важны. Это касается не только физики.

Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.

Сложение проекций. Доказательство главного свойства

Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:

Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:

Давай посчитаем проекции векторов и проекцию вектора их суммы:

Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!

Намного важнее уметь доказывать гипотезы в общем виде.

Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!

Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:

Затем запишем, чему равна сумма этих векторов.

Мы доказали нашу гипотезу.

Но что насчет разности?

Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!

Проекция суммы векторов равна сумме проекций векторов.

Проекция разности векторов равна разности проекций векторов.

Или можно записать так:

Простейшие задачи на нахождение проекций

Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.

Давай научимся с ними работать.

Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.

Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.

В первом случае вектор направлен против оси Х.

Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.

Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!

Рассмотрим второй вектор.

Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.

Убедимся в этом.

На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:

Рассмотрим (vec). Заметим, что он является обратным для (vec): их длины равны, а направления противоположны.

Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:

Поступаем с (vec) так же, как поступали с первым вектором.

Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.

Проведя перпендикуляры, считаем проекцию на ось Y:

С (vec) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:

Задачи на нахождение вектора и его угла с осью

С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.

Давай попробуем это сделать.

Даны проекции вектора на две оси. Для начала нарисуем оси:

Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.

С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?

Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.

Проекция на ось Y положительна. Вектор смотрит в ту же сторону, что и ось.

Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:

Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:

Обозначим угол (alpha ), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?

Рассмотрим смежный ему угол (beta ). Его найти гораздо проще, а в сумме они дадут 180 градусов.

Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла (beta ) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.

Вычитанием угла (beta ) из 180 градусов найдем угол (alpha ):

Главный метод работы с осями и проекциями в решении физических задач

В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.

Поэтому важно научиться искать проекции вектора и связывать их с ней.

Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):

Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.

Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.

Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.

Сделаем это для данного рисунка:

Мы видим, что остальные векторы расположены к осям под каким-то углом.

Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:

Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:

Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.

Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:

Переходим к векторам, которые расположены под углом.

Выглядит страшно, но это не так!

Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.

Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).

Обозначим, что является проекцией. Это катет:

Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.

Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.

Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…

Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Значит, проекцию на ось Х можно найти через косинус.

Не забываем смотреть на направления векторов!

Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.

Видео:Векторные величины Проекция вектора на осьСкачать

Заключение

Итак, теперь мы знаем о векторах очень много! Мы выяснили, зачем они нужны и как с ними работать, а еще разобрали их роль в решении различных задач. Теперь векторы — наша прочная опора.

Именно из таких знаний складывается порой нечто более сложное и комплексное, что-то, что безусловно нам однажды поможет.

Видео:2.1. Скалярные и векторные физические величиныСкачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Физика, 10-й класс, Векторные величины. Действия над векторамиСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Векторные величины Сложение векторовСкачать

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

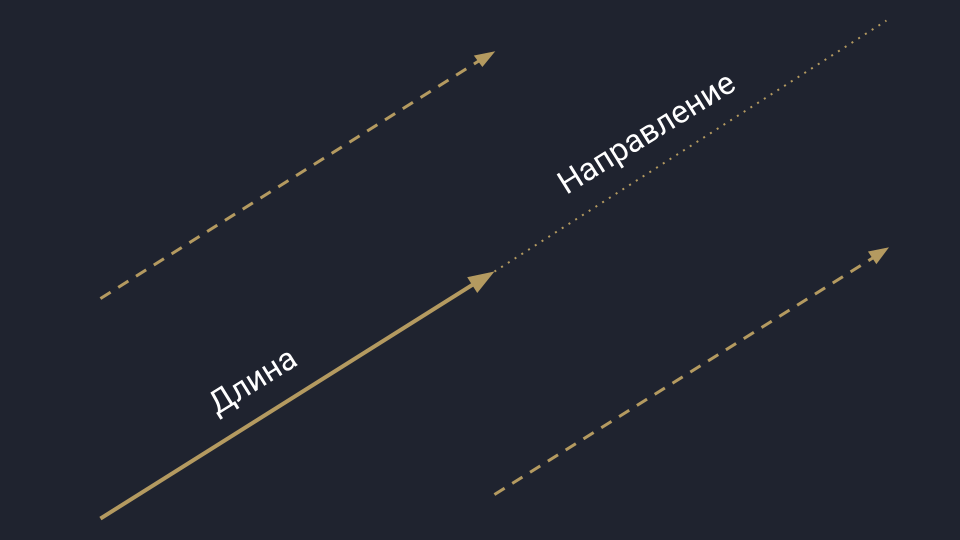
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

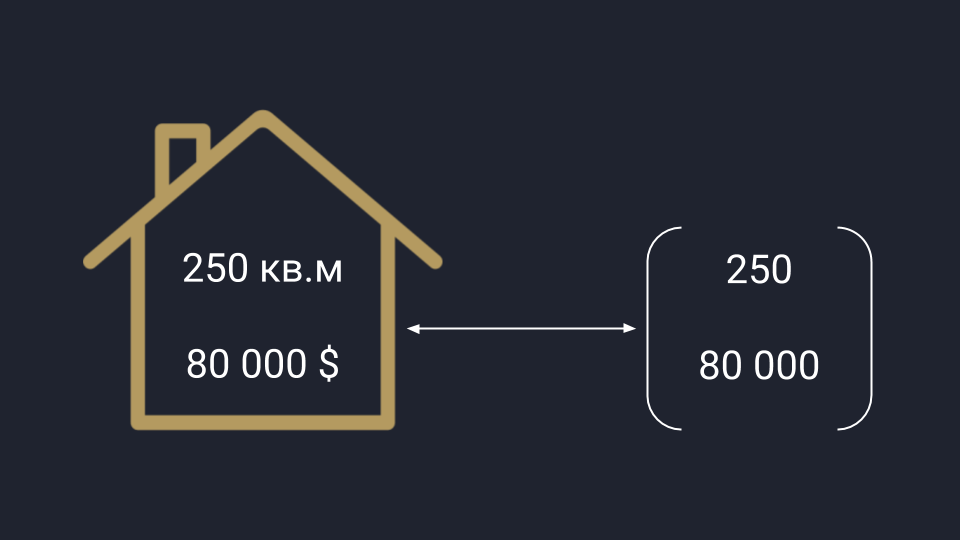
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

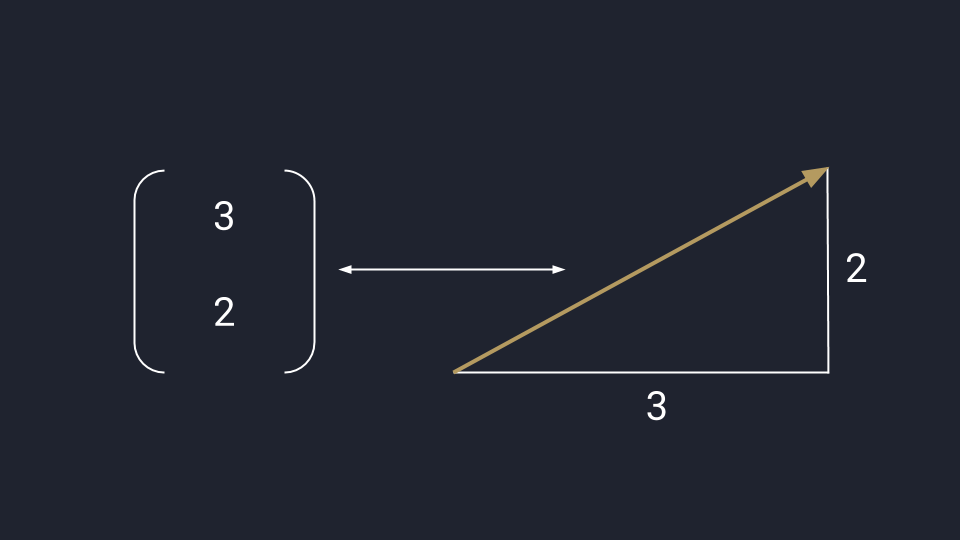
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:Физика.7 класс. Скалярные и векторные физические величины /11.09.2020/Скачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

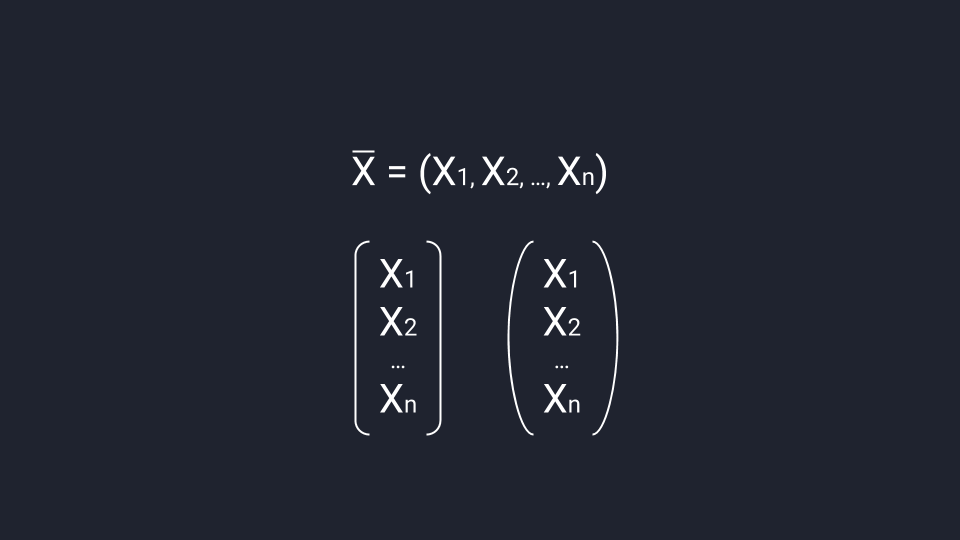
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

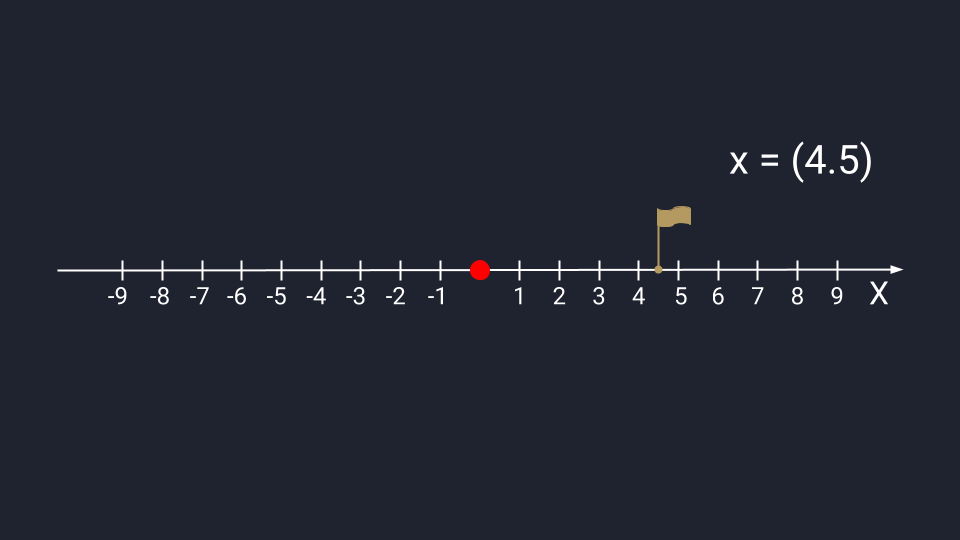
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

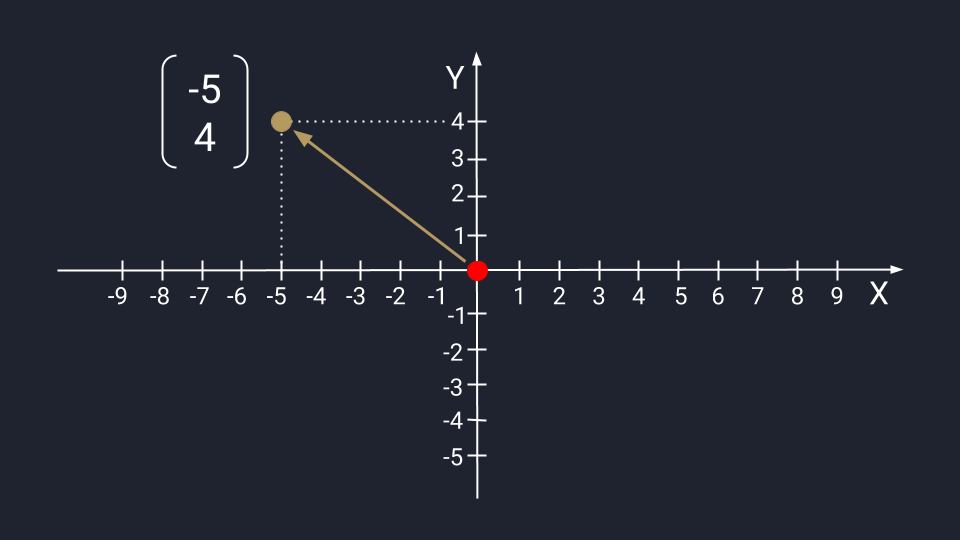
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

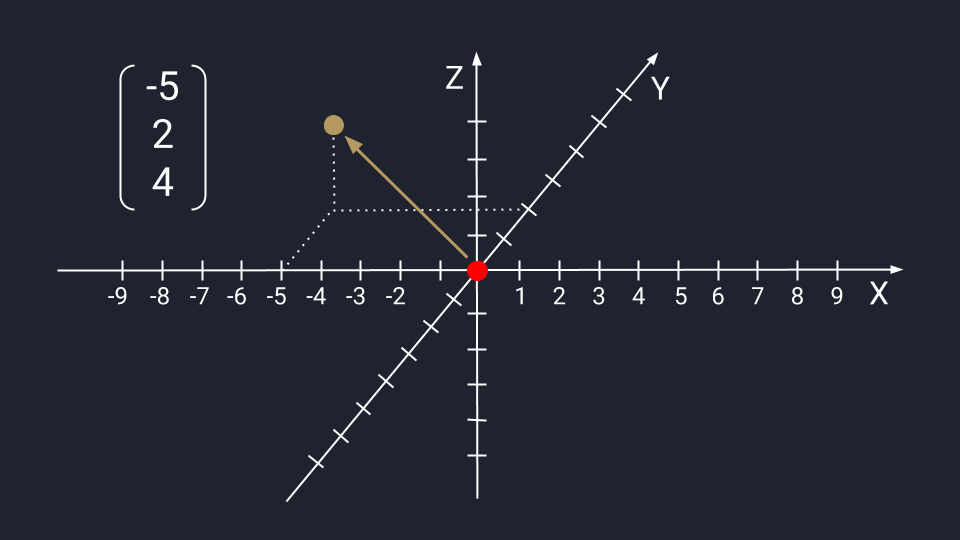
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Вектор в Физике. Как Рисовать Вектор? Модуль Вектора || Урок Физики 8 класс // Подготовка к ЕГЭСкачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.