Функциональная грамотность задачи на окружность

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Окружность. 7 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Формирование функциональной грамотности на уроках геометрии Учитель математики ГБОУ СОШ № 1 п. г. т. Безенчук Шевырялкина Е. В. 2019 г.

Задания со спичками

Задания на развитие геометрической зоркости

Чему равен угол между часовой и минутной стрелками?

Чему равен угол между двумя соседними спицами колеса?

Оказывается, угол, который образует ветвь со стволом плодоносящего дерева (он называется углом отхождения), влияет на плодоношение. Оптимальным углом отхождения скелетных ветвей считается угол 50-60°. Ветви с углом отхождения менее 45° и более 80° рекомендуется удалять.

Смежные и вертикальные углы

С соседом по парте рассмотрите карту вашего города или Москвы – столицы нашей великой Родины (можно воспользоваться яндекс-картами: https://yandex.ru/maps/) и найдите улицы, образующие: а) вертикальные углы; б) смежные углы.

Для измерения высоты дерева используют способ, основанный на равенстве угла падения и угла отражения света. Определите высоту дерева, изображенного на рисунке, если рост человека составляет 1,8 м, а в результате измерений получено: АD = 1,5 м, DЕ = 6 м.

Площади подобных фигур

У одуванчика, выросшего в тени, лист имеет в длину 31 см. У другого экземпляра, выросшего на солнцепеке, длина листовой пластинки всего 3,3 см. Во сколько примерно раз площадь первого листа больше площади второго?

Площадь круга и длина окружности

Планируется на круглую клумбу в парке высадить ирисы и лилии. Вид клумбы показан на рисунке, где большая и малая окружности имеют общий центр, а все части клумбы вне малого круга равны между собой. Диаметры кругов 4 м и 12 м. Сколько ирисов будет посажено на такой клумбе, если на каждый квадратный метр высаживать по 25 ирисов? (Число π взять равным 3,1.)

Колодец цилиндрической формы, имеющий в диаметре 135 см, а глубину 380 м, надо выложить кирпичом. Сколько штук кирпича для этого потребуется, если размер кирпича 25 х 12 х 6,5 см.

Объёмы тел и площади поверхностей

Роман укладывает книги в прямоугольную коробку. Все книги одинакового размера. Какое максимальное количество книг, которое полностью заполнит коробку?

Найдите площадь поверхности шляпы, размеры которой (в см) указаны на рисунке.

Стог сена имеет форму цилиндра с коническим верхом. Радиус его основания 2,5 м, высота 4 м, причем цилиндрическая часть стога имеет высоту 2,2 м. Плотность сена 0,03г/см³. Определите массу стога сена.

Сколько квадратных метров ткани потребуется для пошива шатра цирка «Шапито», если диаметр шатра составляет 32 м, а высота 22 м, причём высота крыши равна 12 м. (Необходимо добавить 5 % на швы и отходы.)

Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение. (В. Произволов)

Краткое описание документа:

Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Например: Каждой группе предлагается решить задачу предложенным способом и доказать правильность своего решения оставшимся группам.При решении компетентностно-ориентированных задач основное внимание должно уделяться формированию способностей учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции. Содержание заданий желательно связывать с традиционными разделами или темами, составляющими основу программ обучения;Для применения на уроке компетентностно-ориентированных заданий могут быть использованы следующие дополнительные возможности изучаемого материала: прикладной характер содержания темы; содержание, включающее в себя оценку явлений и событий; местный материал; содержание программы, связанное с событиями, явлениями, объектами, доступными непосредственному восприятию школьника (в том числе в учебных ситуациях); содержание программы, связанное с формированием учебных умений и навыков; содержание учебного материала, которое может найти применение в воспитательной (внеучебной) деятельности.Компетентностно-ориентированные задания могут использоваться на уроках различных типов: изучения нового материала, закрепления знаний, комплексного применения знаний, обобщения и систематизации знаний, урок контроля, оценки и коррекции.На уроках изучения нового материала с помощью компетентностно-ориентированной задачи можно создать условия для формирования понятий, вывода и усвоения формул.

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Методика преподавания стереометрии как средство формирования функциональной математической грамотности учащихся.

Доклад прочитанный на районном педчтении на тему:»Методика преподавания стереометрии как средство формирования функциональной математической грамотности учащихся «

Просмотр содержимого документа
«Методика преподавания стереометрии как средство формирования функциональной математической грамотности учащихся.»

Методика преподавания стереометрии как средство формирования функциональной математической грамотности учащихся.

Алшева Венера Алимовна,

Одна из важнейших задач современной школы – формирование функционально грамотных людей. Что такое «функциональная грамотность»?

Функциональная грамотность – способность человека вступать в отношения с внешней средой, быстро адаптироваться и функционировать в ней.

Математическая грамотность — способность человека определять и понимать

роль математики в мире, в котором он живет, высказывать хорошо обоснованные

математические суждения и использовать математику так, чтобы удовлетворять в

настоящем и будущем потребности, присущие созидательному, заинтересованному

и мыслящему гражданину.

Термин «грамотность» использован чтобы показать, что изучение состояния

математических знаний и умений, обычно определяемых в школьной программе, не

является первоочередной задачей данного исследования. Основное внимание уделяется

использованию математических знаний в разнообразных ситуациях, применяя

различные подходы, требующие размышлений и интуиции. Очевидно, что для этого

необходимо иметь значительный объем математических знаний и умений, которые

обычно изучаются в школе.

Учащимся в основном предлагаются не учебные, а практические ситуации,

характерные для повседневной жизни (медицина, жилье, спорт и др.). При этом не

ставится цель проверить выделенные знания и умения каждое в отдельности. В большинстве случаев требуется использовать знания и умения из разных тем и разделов

не только курса математики, но и других школьных предметов, например, физики,

В Послании народу Глава государства Н.А.Назарбаев выделил следующее: «Чтобы стать развитым конкурентоспособным государством, мы должны стать высокообразованной нацией. В современном мире простой поголовной грамотности уже явно недостаточно. Наши граждане должны быть готовы к тому, чтобы постоянно овладевать навыками работы на самом передовом оборудовании и самом современном производстве. Необходимо также уделять большое внимание функциональной грамотности наших детей, в целом всего подрастающего поколения. Это важно, чтобы наши дети были адаптированы к современной жизни».

Понятие функциональной грамотности сравнительно молодо: появилось в конце 60-х годов прошлого века в документах ЮНЕСКО и позднее вошло в обиход исследователей. Примерно до середины 70-х годов концепция и стратегия исследования связывалась с профессиональной деятельностью людей: компенсацией недостающих знаний и умений в этой сфере. В дальнейшем этот подход был признан односторонним. Функциональная грамотность стала рассматриваться в более широком смысле: включать компьютерную грамотность, политическую, экономическую грамотность и т.д.

В таком контексте функциональная грамотность выступает как способ социальной ориентации личности, интегрирующей связь образования (в первую очередь общего) с многоплановой человеческой деятельностью.

Рассмотрим несколько вариантов определения функциональной грамотности. Функциональная грамотность (англ. functionalliteracy) – результат образования, который обеспечивает навыки и знания, необходимые для развития личности, получения новых знаний и достижений культуры, овладение новой техникой, успешного выполнения профессиональных обязанностей, организации семейной жизни, в т.ч. воспитания детей, решении различных жизненных проблем.

Функциональную грамотность составляют:

элементы логической грамотности;

умения человека понимать различного рода, касающиеся его государственные акты и следовать им;

соблюдение человеком норм собственной жизни и правил безопасности;

требования технологических процессов, в которые он вовлечен;

информационная и компьютерная грамотность.

Этот начальный уровень функциональной грамотности характерен для передовых цивилизованных обществ. Существует и другой подход к пониманию функциональной грамотности, включающий:

воспитанность человека в духе доброжелательности и дружелюбия, что обеспечивает культуру общения;

В Казахстане был разработан Национальный план действий по развитию функциональной грамотности школьников на 2012-2016гг., утвержденный 25 июня 2012г. Национальный план включает комплекс мероприятий по содержательному, учебно-методическому, материально-техническому обеспечению процесса развития функциональной грамотности школьников. Национальный план призван обеспечить целенаправленность и системность действий по развитию функциональной грамотности школьников как ключевого ориентира для совершенствования качества образования Республики Казахстан. Цель Национального плана – создать условия для развития функциональной грамотности школьников Республики Казахстан.

Задачи Национального плана:

Изучение отечественной и международной практики развития функциональной грамотности школьников.

Определение механизмов реализации системы мер по развитию функциональной грамотности школьников.

Обеспечение модернизации содержания образования: стандартов, учебных планов и программ.

Разработка учебно-методического обеспечения образовательного процесса.

Развитие системы оценки и мониторинга качества образования школьников.

Укрепление материально-технической базы школ и организаций системы дополнительного образования.

Усиление внимания к термину «функциональная грамотность» обусловлено и проводимыми в Казахстане международными исследованиями достижения ожидаемых результатов образования по математике и естественным наукам TIMSS (Third International Mathematics and Science Study) и программе оценки учащихся PISA (Programme for International Student Assessment).

Сегодня перед учителем стоят не совсем простые задачи: создать условия для развития творческих способностей, развивать у учеников стремление к творческому восприятию знаний, учить их самостоятельно мыслить, полнее реализовывать их потребности, повышать мотивацию к изучению предметов, поощрять их индивидуальные склонности и таланты. Развитие самостоятельности, подготовка к взрослой жизни и воспитание личности – вот сверхзадачи, по отношению к которым обучение знаниям, умениям, навыкам выступает как средство образования. Развитие школы напрямую зависит от нас, учителей, нашего творчества, нашей инновационной деятельности, которая находит свое отражение в создании образовательных учреждений нового типа, в разработке и введении новых образовательных технологий, в укреплении и реализации связей с научной общественностью Использование инновационных методов обучения (критическое мышление, методика Ривина, кейс-стади…), индивидуальный подход к каждому ученику, усиление воспитательной функции образования (внеурочная работа), развитие у школьников способности к самоорганизации с целью решения учебных задач помогают грамотно и продуктивно организовать учебный процесс.

Как учитель математики, я прекрасно понимаю важность развития функциональной грамотности моих учеников, вижу в этом с одной стороны насущную необходимость в развитии способности учащихся, применять полученные в школе знания и умения в жизненных ситуациях.

Каждый учитель должен внести вклад в развитие логического и пространственного мышления учащихся. Формирование функциональной грамотности школьников на уроках геометрии возможно через решение задач как в количественном, так и в качественном отношении. Прежде всего важно решить все опорные и простейшие задачи курса, которыми ни в коем случае не стоит пренебрегать. Затем уже стоить переходить к более сложным задачам которые так же в свою очередь можно преобразовать в нестандартные задачи с описанием некоторой близкой к реальной жизни для развития функциональной грамотности.

Ко всему выше сказанному в соей трудовой деятельности, на уроках геометрии я перехожу поэтапно, уделяя особое внимание на рациональное использование времени. Очень большой трудностью при преподавании геометрии является малое количество задач, которые учитель ( сам или со школьниками) успевает решить за время урока. Вызвано это может быть по многим причинам. Для устранения некоторых из таких причин я следую методическим указаниям по преподаванию стереометрии в 10 классе.

Учащиеся воспринимают условие задачи на слух. Конечно, если на каждой парте лежит учебник с этим условием задачи, ученик овладевает навыками быстрого прочтения и уяснения. Если учитель все же хочет сам дать условие задачи, то его представление в конструктивном виде значительно ускоряет ход урока. Приведу пример.

Прямая МС перпендикулярна плоскости прямоугольника АВСD. Расстояние от точки М до других вершин прямоугольника равны 6м,7м и 9м. Найдите длину отрезка МС.

На уроке , не зачитывая это условие, вызвав ученика к доске, можно сказать: «Нарисуйте изображение квадрата АВСD. К его плоскости проведите перпендикуляр МС. Соедините прямыми точки М и D, М и А, М и В. Найдите отрезок МС. »

Пусть не каждый раз, но так давать условие задачи в определенных ситуациях значительно ускоряет ход урока.

Учащиеся затрудняются с чертежом на доске и в тетради и не сразу правильно его делают.

Достаточно часто стереометрический чертеж вообще не делать. Особенно это относится к обучению в 11 классе. Например, такую задачу: «Площадь полной поверхности куба 24 см 2 . Найдите диагональ куба»-не требует чертежа. Не требует чертежа и такая задача: «У пирамиды 28 ребер. Найдите число граней и вершин пирамиды».

Ход урока может быть значительно ускорен применением имеющихся в классе навесных досок с заранее нанесенными на них (не стираемыми) изображениями куба, тетраэдра и т.п. Эти изображения можно подавать на доску при помощи кодоскопа так, чтобы учащемуся осталось только обвести их мелом . Полезно на интерактивной доске показать хорошо выполненные чертежи ( именно чертежи, а не цветные рисунки с тенями) многих геометрических тел. Это даст возможность учащемуся достаточно быстро перерисовать их на доску. Часто процесс урока замедляется из-за неумелого применения геометрических инструментов. Хорошо ,если учащиеся научатся проводить прямые линии без линейки.

Во время практикума по решению задач работа может быть организована так, что класс делится на несколько групп и для каждой группы задается задача для совместного обсуждения и решения задачи.

Во время решения задач на доске можно так организовать работу, чтобы по одному чертежу решить сразу несколько нарастающих по сложности задач и опросить нескольких учащихся .Такой прием качественно ускоряет работу класса и увеличивает количество рассмотренного задачного материала.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формирование функциональной грамотности на уроках математики

Формирование функциональной грамотности на уроках математики

Цель среднего образования: заключается в обеспечении развития у учащихся способностей к познанию, творческому использованию полученных знаний в любой учебной и жизненной ситуации, готовности к саморазвитию и самоуправлению посредством развития ключевых и предметных компетенций.

Современная школа обеспечивает учащихся необходимым багажом, но не всегда формирует умения выходить за пределы привычных учебных ситуаций. Педагоги школы дают сильные предметные знания, но не учат применять их в реальных, жизненных ситуациях. В настоящее время период удвоения знаний составляет 11 лет, а период их «полураспада» не превышает 3-5 лет. Это обусловлено как стремительным развитием науки и техники, так и быстрым моральным устареванием учебной литературы, слабо связанной с проблемами повседневной практики человека.

Хранение и передача знаний, навыков, норм и идеалов, образцов деятельности и поведения, социальных ценностей и ориентаций в системе образования осуществляется через учителя, поэтому к педагогической культуре учителя предъявляются высокие требования, одним из которых является функциональная грамотность.

В Федеральном государственном образовательном стандарте среднего общего образования (10–11‑е классы) (утвержденном приказом Минобрнауки России от 17 апреля 2012 г. № 413) указывается, что в рамках обучения математике (базовый уровень) необходимо добиться у учащихся сформированности представлений о роли и месте математики в современной научной картине мира; понимания математической сущности; понимания роли математики в формировании кругозора и функциональной грамотности для решения практических задач.

Достижения российских школьников в обследовании PISA по математике, оценивающем способность применять полученные знания на практике, остаются скромными: в 2015 году 23-е место (всего 70 стран).

Одним из основных отличительных особенностей реализации стандарта является практическая направленность знаний, накопление и использование жизненного опыта ученика, т.е. не «знания для знаний», а «знания для жизни». Этот общественный заказ уже успешно реализовывает телевидение: образовательные программы, мультфильмы учат действовать в различных жизненных ситуациях.

Требования стандарта таковы, что наряду с традиционным понятием «грамотность», появилось понятие «функциональная грамотность».

Что же такое «функциональная грамотность»?

Функциональная грамотность – «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний».

Функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами.

Основные признаки функционально грамотной личности: это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.

Содержание функциональной грамотности:

· компьютерная и информационная грамотность,

· профессиональные и специальные аспекты функциональной грамотности (менеджмент, PR, бизнес-планирование, новые технологии и т.д.).

Особое место в представлении о функциональной грамотности занимает деятельностная грамотность:

· способность ставить и изменять цели и задачи собственной деятельности,

· реализовывать простейшие акты деятельности в ситуации неопределенности.

Ф ункциональная грамотность отражает общеучебную компетенцию, что на современном этапе обеспечивается за счет внедрения ФГОС на всех уровнях образования. Кроме того, функциональная грамотность упоминается в Концепции развития поликультурного образования в Российской Федерации. В нем подчеркивается, что только функциональная грамотность (владение современной техникой, языками и т.п.) позволяет современному человеку осваивать социальную и природную среду, активно работать в условиях интенсивной экономики и постиндустриальной цивилизации, стать гражданином мира в широком смысле.

Результатом развития функциональной грамотности является овладение обучающимися системой ключевых компетенций, позволяющих молодым людям эффективно применять усвоенные знания в практической ситуации и успешно использовать в процессе социальной адаптации. Ключевые компетенции — это требование государства к качеству личности выпускника основной и средней школы в виде результатов образования, заявленные в федеральном государственном стандарте и учебных программах.

Под математической функциональной грамотностью следует подразумевать способность личности использовать приобретенные математические знания для решения задач в различных сферах.

На уроках математики дети учатся:

• выполнять математические расчеты для решения повседневных задач;
• рассуждать, делать выводы на основе информации, представленной в различных формах (в таблицах, диаграммах, на графиках), широко используемых в средствах массовой информации.

Образование является особой формой мышления, которая, подчиняясь диалектическим законам, поэтапно проводит обучающегося от незнания – к знанию, от владения знаниями – к их применению, а затем – к созданию новых знаний.

Именно поэтому, задания, призванные исследовать состояние математической грамотности учеников, имеют четко выраженную прикладную направленность и их решение предусматривает владение учащимися приемами деятельности прикладного характера.
Состояние математической грамотности учеников оценивается развитием “математической компетентности”. Математическая компетентность определяется как “сочетание математических знаний, умений, опыта и способностей человека”, которые обеспечивают решение разных проблем, нуждающихся в применении математики.

Многие идеи компетентностного подхода появились в результате изучения ситуации на рынке труда и в результате определения тех требований, которые складываются на рынке труда по отношению к работнику. Поэтому школа должна готовить своих учеников к переменам, развивая у них такие качества, как «мобильность, динамизм, конструктивность, инициативность, умение самостоятельно принимать решения»

Для формирования информационной компетентности необходимо использовать задачи содержащие информацию, представленную в различной форме (таблицах, диаграммах, графиках и т.д.). Вопрос задачи может быть сформулирован следующим образом: переведите в графическую (словесную) форму; если возможно, хотя бы приближенно опишите их математической формулой; сделайте вывод, наблюдается ли в этих данных какая-то закономерность и др.

Примером такого задания может быть Задача 1. Аральское море — бессточное солёное озеро в Средней Азии, на границе Казахстана и Узбекистана.

Если обратится к истории Арала, то море уже высыхало, при этом снова возвращаясь в прежние берега. Итак, каким же был Арал несколько последних столетий и как менялись его размеры?

В историческую эпоху происходили существенные колебания уровня Аральского моря. В 1950-х годах Аральское море было четвёртым по площади озером мира, занимая около 68 тыс. км; его длина составляла 426 км, ширина — 284 км, наибольшая глубина — 68 м. Объем Большого Арала и соленость воды рассмотри в таблице.

Рассчитай а) на сколько процентов снизился объём Арала? б) На сколько процентов возросла концентрация воды в море? в) Камбала может жить в морской воде с концентрацией не выше 40%. Водится ли сейчас в Арале камбала?

Заполни пустые клетки в таблице.

содержание воды в %

содержание соли в воде (г/л)

Для формирования коммуникативной компетентности можно использовать групповую форму организации познавательной деятельности учащихся на уроках. Учащимся можно разделиться на несколько групп, каждая группа должна решить задачу предложенным способом и доказать правильность своего решения оставшимся группам.

Задача, которую можно решить, разделившись на группы.

Задача 2. На гипотенузе АВ прямоугольного треугольника АВС построен квадрат ABDE в той полуплоскости от прямой АВ, которой не принадлежит треугольник АВС. Найти расстояние от вершины С прямого угла до центра квадрата, если катеты ВС и АС имеют соответственно длины a и b .

Решить задачу возможно несколькими способами:

1. используя теорему синусов

2. используя теорему косинусов

3. при помощи метода площадей

4. при помощи метода координат

Д Е

В Решение 1 (используя теорему синусов).

Пусть О — центр построенного квадрата. А

Так как угол A О B прямой, то точка О

лежит на описанной около треугольника АВС

окружности. Ее диаметром служит гипотенуза АВ. Из треугольника A О C по теореме синусов имеем:

СО = АВ sin (α+45°), где α – величина угла ВАС. Далее получаем:

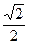
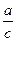
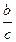
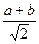
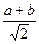
C О= c ( sinαcos 45°+ cosαsin 45°) = c ( + ) = , где с = АВ. Итак, искомое расстояние C О равно .

Решение 2 ( используя теорему косинусов).

Из того же треугольника A О C по теореме косинусов находим:

C О 2 = b 2 + A О 2 – 2 b ∙ C О cos ( α +45°).

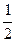
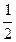
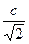
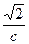
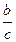
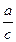
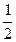
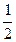
Рассмотрим треугольник A О B , который является прямоугольным и равнобедренным ( B О=О A ). По теореме Пифагора находим, что A О 2 = c 2 . Тогда

C О 2 = b 2 + c 2 – 2b∙ ∙ ( — ) = b 2 + (a 2 + b 2 ) – b 2 + ab = (a +b) 2 ,

СО = .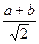

Решение 3 ( при помощи метода площадей).

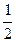
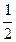
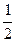
Сумма площадей треугольников АВС и AB О равна площади четырехугольника A О BC : ab + A О 2 = c ∙ C О sinφ ,

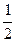
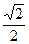
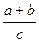
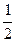
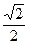
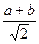
где φ – величина угла между прямыми AB и C О. Луч C О есть биссектриса угла АСВ, так как вписанные углы AC О и BC О опираются на равные дуги A О и B О.По теореме о внешнем угле треугольника φ = α + 45°. Подставив в предыдущее равенство A О 2 = ( a 2 + b 2 ) и sinφ = ∙ (по решению 1), получим: ab + ( a 2 + b 2 ) = C О∙ ( a + b ) и C О = .

Решение 4 (при помощи метода координат).

Примем прямые СА и СВ за оси Ох и Оу прямоугольной декартовой системы координат. Найдем координаты х, у точки О. Она принадлежит биссектрисе угла АСВ (по решению 3) и равноудалена от точек A ( b ,0) и B (0, a ). Имеем систему: х = у

( x — b ) 2 + у 2 = х 2 + (у — а) 2 ,

откуда 2х( b — а ) = b 2 – a 2 (подставив первое равенство во второе).

Если a ≠ b , то имеем решение х = у = .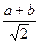

При a = b четырехугольник A О BC является квадратом и х = у =а, т.е. координаты точки О удовлетворяют прежнему решению. По формуле расстояния между двумя точками C О = = = .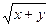

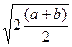
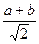
Для формирования исследовательской компетентности учащимся можно предложить задания, в которых необходимо исследовать все возможные варианты и сделать определенный вывод.

Задача 3 . «Треугольники»

Треугольник PQR прямоугольный с прямым углом R. Сторона RQ меньше стороны PR. M – середина стороны PQ и N – середина стороны QR.

S – точка внутри данного треугольника. Отрезок MN больше отрезка MS.

Обведите букву, которой обозначена фигура.

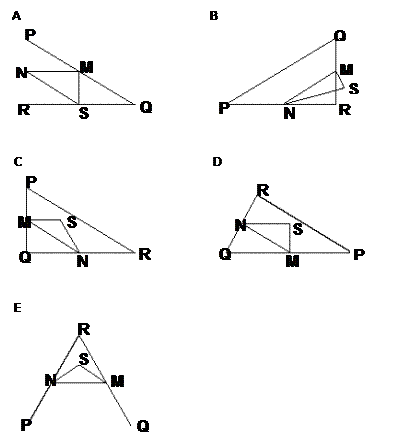Готовность к разрешению проблем формируется с помощью задач, в которых необходимо проанализировать предложенную ситуацию, поставить цель, спланировать результат, разработать алгоритм решения задачи, проанализировать результат.

Твои родители решили отпраздновать день рождения твоего брата в кафе «Тобол». Было решено, что их расходы не должны превышать 100 000 тен г е. Используя предложенные источники, произведите необходимые расчеты, сделайте вывод и дайте практические рекомендации родителям.

Для начала родители подготовили список приглашенных на празднование дня рождения сына Сергея. Они решили праздновать его день рождения в кафе «Тобол», поэтому они взяли прейскурант цен на заказ блюд, напитков, на обслуживание и на дополнительные услуги в данном кафе.

Было решено отмечать день рождение с 16.00 до 22.00. На совете семьи составили меню и список приглашенных

1. Мария Владимировна (мама)

2. Петр Сергеевич (папа)

3. Сергей (именинник)

4. Марина (младшая сестра)

1. Зоя Васильевна (бабушка)

2. Дмитрий Федорович (дядя)

3. Миша (двоюродный брат)

4. Света (двоюродная сестра)

2. Ковалев Максим

3. Карташова Лиза

Прейскурант цен на заказ блюд

Бутерброды с бужениной

Бутерброды с помидорами

Бутерброды с паштетом и яблоками

(хлеб, сельдь, картофель, огурцы, лимон, майонез)

(хлеб, сливочное масло, твердый сыр, петрушка)

Бутерброды с сыром и фруктами

Канапе с ветчиной и огурцом

Канапе с сельдью и яблоками

Канапе с лососиной

Канапе с языком и сыром

Канапе с грибами и яйцом

Салат из ананаса с сельдереем

(ананас, сельдерей, свекла, салат, растительное масло)

(помидор, огурцы, спаржа, фасоль, зеленый горошек, цветная капуста, салат, майонез)

(мясо, огурцы, зеленый лук, яйца, зелень, майонез)

Салат с сельдью и крабами

(сельдь, картофель, соленые огурцы, морковь, лук, крабы, салат, горчица, майонез)

(мясо птицы, картофель, соленые огурцы, салат, маслины, соус «Южный», майонез)

Суп – пюре из куриной печени

Суп рыбный с фрикадельками

Бифштекс с картофелем

Шашлык из молодой баранины

Зразы из говяжей вырезки

Цыплята, жаренные в тесте

Зразы из рыбы и грибов под соусом

Треска по — польски

Осетрина, запеченная с грибами

Карпы, жаренные во фритюре

Пудинг из сливок и бисквита

Шарлотка из яблок

Мусс из апельсинов

Самбук из яблок

Торт слоеный с вареньем и взбитыми сливками

Персики в креме

Сливочный пломбир с ананасом и дыней

Пломбир с вареными грушами и ореховым печеньем

Какао с мороженым

Коктейль фруктовый с мороженым

Актер (в костюме клоуна, скомороха и т. п.)

Музыкальное оформление (магнитофон)

Украшение зала (шары, цветы, плакаты)

(по заказу клиента)

Для формирования готовности к самообразованию учащимся необходимо предлагать самостоятельно изучить некоторый теоретический материал, написать реферат, составить задачу и т.д.

Математика встречается в решении бытовых задач, задач экономики, сельского хозяйства, научных исследованиях, технических вопросах.

Вот примеры задач, которые были составлены учениками 5 классов и их родителями.

Задача № 10 Аптека

Моя тетя фармацевт. Она работает в аптеке. Продает лекарства. Вот задача, которую предложила решить моя тетя.

Больному прописали лекарство, которое нужно принимать по 0,5 таблетки 4 раза в день на протяжении 14 дней. Лекарство продается в упаковках по 10 таблеток. Какое количество упаковок требуется на весь курс лечения?

1) 0,5*4=2(таблетки) надо пить каждый день

2) 2*14 = 28(таблеток) на 14 дней

3) так как в упаковке 10 таблеток, то надо купить 3 упаковки или 30 таблеток Ответ: 3 упаковки

Оцени и рассчитай, сколько рулонов обоев шириной 50см и длиной 15м потребуется для оклейки стен твоей комнаты. Площадь пола, которой равна 4х4 м 2 , высота — 2,5м, размеры двери 2х1м, окна 1х1,5м

Задача № 14 Строительство

Твои родители планируют летом застелить двор брусчаткой.

Реши, в каком магазине вам выгоднее купить брусчатку

Магазин «Мегастрой»: 1 квадратная плитка со стороной 15см стоит 33 тг

Магазин «Стройматериалы»: правильная 6-угольная плитка, 1 кв.м-1600 тг,.

Задача № 8 Банковское дело

Клиент банка открыл депозит на сумму500000 тг, со ставкой вознаграждения 9% годовых. Сколько составит начисленное вознаграждение по депозиту через 8 месяцев?

1)500000*0,09 = 45000(тг) начисление вознаграждения за год (12 месяцев)

2) 45000:12*8 = 30000(тг) вознаграждение за 8 месяцев

Задача № 9 Стоимость продуктов через год

Сейчас молоко стоит 170 тг, Каждые полгода инфляция составляет 10% Сколько будет стоить молоко через год?

1) 170*0,1=17(тг) составляет 10% стоимости молока.

2) 170+17=187 (тг) молоко будет стоить через пол года

3) 187*0,1=18,7(тг) составляет 10% стоимости молока.

4) 187+18,7 =205,7(тг) молоко будет стоить через год.

Ответ: 205 тенге 7тиын

Задача № 3 Пекарь

Из 3,2 кг ржаной муки получается 4,2 кг хлеба. Каждая булка весит 0,6кг. Сколько можно выпечь булок из 12,8 кг муки?

1) 4,2:0,6=7 булок можно спечь из 3,2 кг муки

2) 12,8:3,2 = 4 во столько раз больше булок можно испечь

3) 7*4=28 булок можно спечь из 12,8 кг муки

Составляя эти задачи, дети развивают функциональную грамотность, видят применение математических знаний в жизни.

ª Формирование ключевых компетентностей посредством задач позволяет реализовать компетентностный подход на уроках математики как средство повышения математической грамотности учащихся.

Часто одна и та же задача способствует созданию условий для формирования нескольких ключевых компетентностей.

Задач, способствующих формированию ключевых компетентностей, в учебниках и дидактических пособиях немного. Поэтому для реализации компетентностного подхода через задачи единственным выходом для школьных учителей является составление компетентностно-ориентированных задач самим.

Рассмотрим несколько примеров использования задач из учебника, с помощью которых можно составить задание для формирования ключевых компетентностей учащихся.

Антон, Илья и Никита собрали 152 марки. Антон собрал в 3 раза больше марок, чем Никита, а Илья в 4 раза больше, чем Никита. Сколько марок собрал каждый мальчик?

Эта задача не является компетентностно-ориентированной задачей. Добавив к условию задачи вопрос «постройте круговую диаграмму, изображающую распределение марок (в процентах)», задание становится компетентностно-ориентированной задачей.

Задача В романе Жюля Верна «Дети капитана Гранта» читаем: «Погода стояла прекрасная, не слишком жаркая…Роберт узнал, что средняя годовая температура в провинции Виктория +74 о по Фаренгейту». Сколько это будет в привычных для нас градусах Цельсия? Составьте формулу для вычисления температуры в градусах Цельсия, если известна температура по Фаренгейту и наоборот.

В таблице приведена температура таяния льда и кипения воды в градусах Цельсия и по Фаренгейту»

В градусах Цельсия

Эта задача является заданием первого уровня, так как учащимся необходимо с помощью таблицы составить формулу и используя эту формулу ответить на вопрос задачи. Для того чтобы задача стала заданием второго уровня, добавим в условие задачи несколько вопросов.

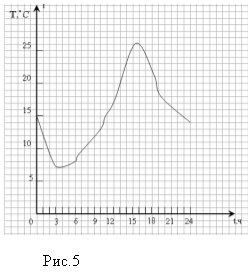
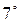
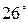
Например : Температура воздуха изменялась в течение дня от до Цельсия. На рисунке 5 изображен график изменения температуры. Изобразите график функции, на котором будет изображена температура воздуха в градусах по Фаренгейту, соответствующая температуре на графике.

Эта задача будет заданием второго уровня, так как в ходе решения задачи учащимся необходимо определить значения величин по графику и результатом решения задачи так же будет график.

Задача «Редактор школьной стенгазеты поместил заметку: «На школьных соревнованиях быстрее всех пробежал стометровку ученик 7 «В» класса Аскар. Другие призеры пришли к финишу в таком порядке: Аслан, Паша, Дима. И удивительно – с одной и той же разницей в скорости: Аскар затратил на эту дистанцию 12 с, Аслан – 13 с, Паша – 14 с, Дима – 15 с».

Проверьте, прав ли наш «журналист». Для этого заполните таблицу :

В последней строке поместите разность скоростей каждого мальчика и предыдущего. Действительно ли разница в скорости одна и та же?».

Эта задача является заданием второго уровня, так как решение задачи будет состоять из нескольких шагов, учащимся нужно сравнить получившиеся результаты. Для того, чтобы задача стала заданием третьего уровня можно к условию добавить вопрос: скорость какого из мальчиков ближе к средней скорости бегунов? Результат представьте в виде диаграммы.

Таким образом, задачи из учебника можно использовать в качестве основы для компетентностно-ориентированных заданий.

Основное противоречие учебной деятельности учащихся средних классов. Результаты наблюдений, проведенные за последние четыре года в школах России, позволяют сделать вывод о том, что затруднения в начале изучения систематических курсов алгебры и геометрии в большой степени обусловлены дефицитами учебной деятельности учащихся, накопленными в предыдущие годы обучения. В рамках реального учебного процесса проявления этих дефицитов имеют комплексный характер, например отсутствие самостоятельной деятельности учащихся на уроке (исключение могут составить учащиеся, идущие по учебной линии Л.Г. Петерсона).

Задача формирования естественнонаучной грамотности и достижения образовательных результатов ФГОС предъявляет определённые требования к содержанию учебной деятельности на уроке и необходимым компетенциям учителя. Развитие профессиональной компетентности учителя, обеспечивающей реализацию педагогического процесса, инициирующего и формирующего функциональную грамотность учащегося, является на современном этапе развития образования одной из главных задач.

Формирования функциональной грамотности учащихся основной школы обеспечивается и достигается, если:

— рассматривать функциональную грамотность учащихся как базовый уровень образованности учащихся, характеризующий степень овладения способами работы с информацией и позволяющий решать реальные жизненные проблемы, адаптироваться к внешнему миру;

— включить в состав профессиональной компетентности учителя по формированию функциональной грамотности учащихся три составляющих: когнитивный, операционально-технологический и личностный компоненты, опирающиеся на функциональную грамотность ученика;

— реализовать содержание профессиональной компетентности учителя по формированию функциональной грамотности учащихся в процессе повышения квалификации в условиях внутришкольной методической работы;

— разработать, обосновать и апробировать интерактивную технологию развития профессиональной компетентности учителя по формированию функциональной грамотности учащихся;

— выявить совокупность организационно-педагогических условий, обеспечивающих развитие профессиональной компетентности учителя по формированию функциональной грамотности учащихся.

Целенаправленное формирование умений решать задачи вообще, математические в частности, является, безусловно, одним из важнейших путей усовершенствования образования. А это, в свою очередь, связано с формированием навыков анализа условия задачи, поиска путей её решения, осмысления результатов решения.

Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы является слишком большим с общеобразовательных позиций, а качество владения ими – недостаточно высоким. А главное, формирование этой системы знаний и умений не связана органически с формированием умений применять математику и стратегией решения задач.

Успешное выполнение контекстных заданий может быть обеспечено только при ориентации учебного процесса на решение подобных задач.

Чтобы повысить математическую грамотность учащихся, можно предложить учащимся самим составить задачи и уравнения, ребусы, кроссоворды, разноуровневые задания.

В связи с этим давайте все запомним одну математическую формулу, которая позволит сформировать у учащихся в процессе изучения математики и других дисциплин качества мышления, необходимые для полноценного функционирования человека в современном обществе.

«ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ»

Реализация Национального плана позволит обеспечить общую координацию деятельности государственных органов, профессионального сообщества, неправительственных организаций, родителей по развитию функциональной грамотности школьников.

В результате выполнения Национального плана к 2017 году были созданы следующие условия для развития функциональной грамотности школьников:

1. Научно-исследовательское обеспечение:
1) определены научно-методологические основы формирования и развития функциональной грамотности, системы управления школой в парадигме компетентностного образования;
2) обеспечено научно-исследовательское, экспертно-аналитическое сопровождение мероприятий, направленных на формирование и развитие функциональной грамотности;
3) обеспечена диагностика смысла жизненных ориентации школьников, роли родителей в формировании функциональной грамотности детей.

Концепция обновления современной школы определила новые приоритеты общего образования, которые предполагают, что формирование модели учебного процесса должно осуществляться на основе развития взаимоотношений сотрудничества учителя и ученика, гармоничного сочетания различных методов обучения, обеспечивающих использование разнообразных видов учебной деятельности. Эти приоритеты составляют основу развития и современного школьного образования. В соответствии с ним уточнены учебно-воспитательные цели обучения на каждой ступени школы, принципы отбора структурирования содержания, а также методы оценки качества подготовки школьников.

🎥 Видео

Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Геометрическая задача как инструмент формирования функциональной грамотности. Система задСкачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Что такое функциональная грамотность?Скачать

Окружность. Вебинар | МатематикаСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Функциональная математическая грамотность. Часть 1. Задачи №№ 1-5. Математика. 6 классСкачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать