Вектор а равен 2 вектор б равен 3 угол между ними 120 (8 видео)

Задача 22492 1. Даны векторы vector и vector и.

Содержание

Условие
Решение
Угол между векторами.
Формула вычисления угла между векторами
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Примеры вычисления угла между векторами для пространственных задач
Нахождение угла между векторами: онлайн калькулятор
Как найти угол между векторами с помощью онлайн-калькулятора
📺 Видео

Условие

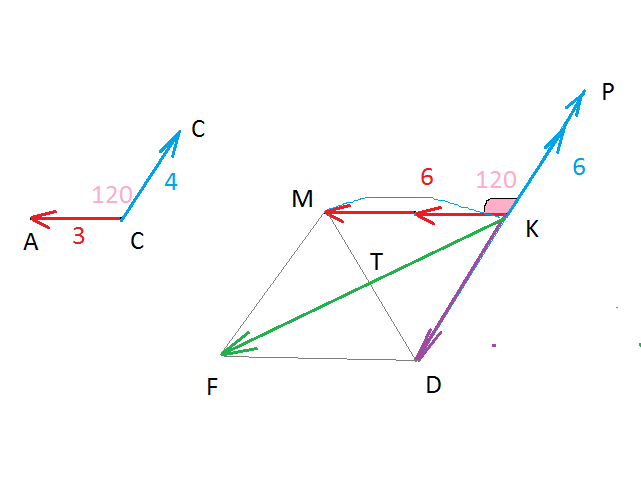
1. Даны векторы vector и vector и угол между ними равный 120°. Построить вектор vector = 2vector-1,5vector и определить его длину, если |vector| = 3, |vector| = 4.

Решение

Откладываем векторы от одной общей точки С
vector=vector
vector=vector

∠MKD=60 градусов, как смежный углу в 120 градусов.

Δ МKD — равнобедренный с углом 60 градусов при вершине, значит и другие его углы по 60 градусов и он равносторонний.

KT- высота равностороннего треугольника со стороной 6
КТ=6*sin60 градусов=6sqrt(3)/2=3sqrt(3)

|vector|=6sqrt(3)
О т в е т. 6sqrt(3)

Видео:Угол между векторами. 9 класс.Скачать

Угол между векторами.

Вектор а равен 2 вектор б равен 3 угол между ними 120

Видео:Угол между векторами | МатематикаСкачать

Формула вычисления угла между векторами

cos α =	a · b
	\| a \|·\| b \|

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5

Найдем угол между векторами:

cos α =	a · b	=	24	=	24	= 0.96
	\| a \| · \| b \|		5 · 5		25

Решение: Найдем скалярное произведение векторов:

a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α =	a · b	=	40	=	40	=	4	= 0.8
	\| a \| · \| b \|		5√ 2 · 5√ 2		50		5

Примеры вычисления угла между векторами для пространственных задач

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6

Найдем угол между векторами:

cos α =	a · b	=	28	=	14
	\| a \| · \| b \|		5 · 6		15

Решение: Найдем скалярное произведение векторов:

a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:11 класс, 5 урок, Угол между векторамиСкачать

Нахождение угла между векторами: онлайн калькулятор

Два вектора всегда образуют угол. Чтобы найти угол между двумя векторами на плоскости или в пространстве, нужно использовать формулу для скалярного произведения и знать длины векторов. Сначала вычисляется косинус угла между векторами, затем находится и сам угол.

Чтобы найти угол между векторами онлайн, не нужно самостоятельно производить громоздкие вычисления. Достаточно просто задать два вектора в удобной форме (точки или координаты) и нажать кнопку «рассчитать».

Видео:найти угол между единичными векторамиСкачать

Как найти угол между векторами с помощью онлайн-калькулятора

Для нахождения угла между векторами с помощью нашего онлайн-калькулятора выполните несколько простых действий:

Укажите размерность векторов. Это может быть плоскость или пространство.
Определитесь с формой представления векторов. Их можно задать координатами либо точками:
В соответствующие поля введите значения векторов и нажмите «Рассчитать».
Рассмотрим наглядный пример с произвольными значениями. Пусть у нас есть два вектора на плоскости, заданные координатами:

После того, как мы нажмем «Рассчитать», калькулятор выдаст решение с пояснением: