Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Ваш ответ
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

решение вопроса
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,688
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Чему равна сумма углов выпуклого многоугольникаСкачать

Тема: «Параллелограмм. Решение задач»
МОУ «Средняя общеобразовательная школа с. Куриловка
Предмет: математика (геометрия)
Методическая тема: Технология уровневой дифференциации на уроках математики.
Тип урока: урок применения знаний и умений.
Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач;
развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
содействовать развитию у учащихся чувства ответственности за деятельность коллектива и в коллективе;
содействовать развитию коллективного общения учащихся;
содействовать развитию у учащихся интереса к математике.
Элементы урока и их содержание
Сообщают об отсутствующих.
Сегодня на уроке мы закрепим знания о свойствах и признаках параллелограмма в процессе решения задач.
Сообщает дату проведения урока, тему урока, цель урока.
Записывают в тетради.
III.Проверка домашнего задания
1) Дайте определение параллелограмма.
2) Перечислите свойства параллелограмма.
3) Перечислите признаки параллелограмма.
Проводит опрос учащихся
Учащиеся отвечают на вопросы.
1)Решение задач разного уровня сложности (приложение 1)
2) Проверка заданий.
3)Устное решение задач по готовым чертежам (приложение 2)
1)Следит за верностью решения у слабых учащихся, задавая им наводящие вопросы.
2) Проверяет решение задач II и III уровня сложности. Выставляет оценки за работу.
2)Следит за верностью рассуждений при решении устных задач.
Учащихся работают на местах.
Самостоятельная работа (приложение 3):
Сильные учащиеся работают самостоятельно (решают задачи II и III уровня).
Слабоуспевающие учащиеся работают вместе с учителем.
Следит за верностью решения у слабоуспевающих учащихся.
Выполняют работу в тетрадях.
VI. Подведение итогов. Рефлексия.
Выставляет оценки за работу.
№ 000, 380, 384 (устно)
Поясняет домашнее задание.
Внимательно слушают, записывают в дневники.
1. Точки E и K — середины сторон AB и CD параллелограмма ABCD. Докажите, что AECK – параллелограмм.
2. Диагонали четырёхугольника ABCD пересекаются в точке O, причём AC = 2 дм, AO = 10 см,
BD = 1,5 дм, BO = 7 см. Выясните, является ли ABCD – параллелограммом?
1. В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и N так, что ﮮ BMC = ﮮ AND. Докажите, что AMCN – параллелограмм.
2. Точки A и B делят диагональ MK параллелограмма MNKP на три равные части. Является ли четырёхугольник ANBP параллелограммом? Ответ обоснуйте.
1. В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и K так, что AM=CK, а на сторонах BC и AD – точки N и P так, что AP=CN. Докажите, что MNKP – параллелограмм.
2. Через точку пересечения диагоналей O параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и BC в точках M и N соответственно. Является ли четырёхугольник MBND параллелограммом? Ответ обоснуйте.
1. ABCD – параллелограмм. Найти: ﮮ C, ﮮ D.
2. MNKP – параллелограмм. Найти: MP, PK.
3. ABCD – параллелограмм. Найти:ﮮA,ﮮB, ﮮ C, ﮮ D.
4. ABCD – параллелограмм. Найти:PABCD.
5. ABCD – параллелограмм. Найти:AD.
6. ABCD – параллелограмм. Найти: PABCD, ﮮAED.
7. NBFD – параллелограмм. Найти: BC, СD.
8. ABCD – параллелограмм, PMNKP,=20 см. Найти: MN, MP.
9. BNDM – параллелограмм, AB:BC=4:5, PABCD,=18 см. Найти: AD, DC.
1. В четырехугольнике ABCD AB||CD, BC||AD, AC=20см, BD=10см, AB=13 см. Диагонали ABCD пересекаются в точке O. Найдите периметр ΔCOD.
2. Из вершины B параллелограмма ABCD с острым углом A проведён перпендикуляр BK к прямой AD, BK=AB:2. Найдите ﮮC, ﮮD.
3. Середина отрезка BD является центром окружности с диаметром AC, причём точки A, B, C, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.
1. В четырехугольнике ABCD AB||CD, BC||AD, O – точка пересечения диагоналей. Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
2. В параллелограмме ABCD с острым углом A из вершины B проведён перпендикуляр BK к прямой AD, AK=BK. Найдите ﮮC, ﮮD.
3. Дан параллелограмм ABCD. На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM=CN. Докажите, что MBND – параллелограмм.
1. В четырехугольнике ABCD ﮮA+ﮮB=180°, AB|| CD. На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
2. На сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно, MP=PB=AK; ﮮMPB=60°. Найдите углы параллелограмма и сравните отрезки BM и AH.
3. На основании AC равнобедренного треугольника ABC отмечена точка K, а на сторонах AB и BC – точки M и P соответственно, причём PK=MB, ﮮKPC=80°, ﮮC=50°. Докажите, что KMBP – параллелограмм.
1. В четырехугольнике MPKH ﮮPMK=ﮮHKM, PK||MH. Через точку пересечения диагоналей проведена прямая, пересекающая стороны PK и MH в точках A и B соответственно. Докажите, что AP=HB.
2. На сторонах BC и AD параллелограмма ABCD взяты точки M и K, AB=BM=KD; ﮮAMB=30°. Найдите углы параллелограмма и сравните отрезки AM и CK.
3. В ΔMPK ﮮM=65°. На сторонах MK, MP, PK отмечены точки A, B, C соответственно так, что середина стороны PK – точка C, AM=KC, BP=AC, ﮮBAM=50°. Докажите, что BPCA – параллелограмм.
1. В выпуклом четырехугольнике ABCD ﮮA+ﮮB=ﮮB+ﮮC=180°. Через точку O пересечения диагоналей четырёхугольника проведена прямая, пересекающая стороны DC и AD в точках M и K соответственно; ﮮBOM=90°.
Докажите, что BK=BM.
2. На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно так, что отрезки BH и MD пересекаются в точке O; ﮮBHD=95°, ﮮDMC=90°, ﮮBOD=155°. Найдите отношение длин отрезков AB и MD и углы параллелограмма.
3. Точки M и K являются соответственно серединами сторон AB и BC треугольника ABC. Через вершину C вне треугольника проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE=AC:2.
1. В выпуклом четырехугольнике MPKH ﮮM+ﮮP=180°, ﮮMKH=ﮮKMP. На сторонах MH и PK отмечены точки A и B так, что PB=PA. Отрезок AB проходит через точку пересечения диагоналей четырёхугольника. Докажите, что HP перпендикулярен AB.
Докажите, что BK=BM.
2. На сторонах BC и CD параллелограмма ABCD взяты точки K и M соответственно. Отрезки BM и KD пересекаются в точке O; ﮮBOD=140°, ﮮDKB=110°, ﮮBMC=90°. Найдите отношение длин отрезков MC и AD и углы параллелограмма.
3. Точки A и B принадлежат соответственно сторонам PE и ET треугольника PET. Прямая, проходящая через вершину T вне треугольника, пересекает луч AB и точке K так, что AP=KT, AB=BK=PT:2. Докажите, что точка A является серединой отрезка PE.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Технология уровневой дифференциации на уроках математики
Главная > Урок
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
МОУ «Средняя общеобразовательная школа с. Куриловка
Вольского района Саратовской области»
Учитель : Кузнецова Татьяна Ивановна
Предмет : математика (геометрия)
Тема : Параллелограмм . Решение задач.
Методическая тема : Технология уровневой дифференциации на уроках математики.
Тип урока: урок применения знаний и умений.
Закрепить знания о свойствах и признаках параллелограмма в процессе решения задач;
развивать логическое мышление, память, познавательный интерес; продолжать формирование математической речи; вырабатывать умение анализировать и сравнивать;
содействовать развитию у учащихся чувства ответственности за деятельность коллектива и в коллективе;
содействовать развитию коллективного общения учащихся;
содействовать развитию у учащихся интереса к математике.
Элементы урока и их содержание
I .Организационный этап
Сообщают об отсутствующих.
II .Постановка цели
Сегодня на уроке мы закрепим знания о свойствах и признаках параллелограмма в процессе решения задач.
Сообщает дату проведения урока, тему урока, цель урока.
Записывают в тетради.
III .Проверка домашнего задания
Дайте определение параллелограмма.
Перечислите свойства параллелограмма.
Перечислите признаки параллелограмма.
Проводит опрос учащихся
Учащиеся отвечают на вопросы.
IV . Решение задач
1)Решение задач разного уровня сложности (приложение 1)
2) Проверка заданий.
3)Устное решение задач по готовым чертежам (приложение 2)
1)Следит за верностью решения у слабых учащихся, задавая им наводящие вопросы.
2) Проверяет решение задач II и III уровня сложности. Выставляет оценки за работу.
2)Следит за верностью рассуждений при решении устных задач.
Учащихся работают на местах.
Самостоятельная работа (приложение 3):
Сильные учащиеся работают самостоятельно (решают задачи II и III уровня).
Слабоуспевающие учащиеся работают вместе с учителем.
Следит за верностью решения у слабоуспевающих учащихся.
Выполняют работу в тетрадях.
VI . Подведение итогов. Рефлексия.
Выставляет оценки за работу.
VII . Домашнее задание:
№375, 380, 384 (устно)
Поясняет домашнее задание.
Внимательно слушают, записывают в дневники.
Точки E и K — середины сторон AB и CD параллелограмма ABCD. Докажите, что AECK – параллелограмм.
Диагонали четырёхугольника ABCD пересекаются в точке O, причём AC = 2 дм, AO = 10 см,
BD = 1,5 дм, BO = 7 см. Выясните, является ли ABCD – параллелограммом?
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и N так, что ﮮ BMC = ﮮ AND. Докажите, что AMCN – параллелограмм.
Точки A и B делят диагональ MK параллелограмма MNKP на три равные части. Является ли четырёхугольник ANBP параллелограммом? Ответ обоснуйте.
В параллелограмме ABCD на сторонах AB и CD отмечены соответственно точки M и K так, что AM=CK, а на сторонах BC и AD – точки N и P так, что AP=CN. Докажите, что MNKP – параллелограмм.
Через точку пересечения диагоналей O параллелограмма ABCD проведена прямая MN, пересекающая стороны AD и BC в точках M и N соответственно. Является ли четырёхугольник MBND параллелограммом? Ответ обоснуйте.
ABCD – параллелограмм. Найти: ﮮ C, ﮮ D.
MNKP – параллелограмм. Найти: MP, PK.
ABCD – параллелограмм. Найти:ﮮA,ﮮB, ﮮ C, ﮮ D.
ABCD – параллелограмм. Найти:P ABCD .
ABCD – параллелограмм. Найти:AD.
ABCD – параллелограмм. Найти: P ABCD , ﮮAED.
NBFD – параллелограмм. Найти: BC, СD.
ABCD – параллелограмм, P MNKP ,=20 см. Найти: MN, MP.
BNDM – параллелограмм, AB:BC=4:5, P ABCD ,=18 см. Найти: AD, DC.
В четырехугольнике ABCD AB||CD, BC||AD, AC=20см, BD=10см, AB=13 см. Диагонали ABCD пересекаются в точке O. Найдите периметр ΔCOD.
Из вершины B параллелограмма ABCD с острым углом A проведён перпендикуляр BK к прямой AD, BK=AB:2. Найдите ﮮC, ﮮD.
Середина отрезка BD является центром окружности с диаметром AC, причём точки A, B, C, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.
В четырехугольнике ABCD AB||CD, BC||AD, O – точка пересечения диагоналей. Периметр ΔAOD равен 25 см, AC=16см, BD=14см. Найдите BC.
В параллелограмме ABCD с острым углом A из вершины B проведён перпендикуляр BK к прямой AD, AK=BK. Найдите ﮮC, ﮮD.
Дан параллелограмм ABCD. На продолжении диагонали AC за вершины A и C отмечены точки M и N соответственно так, что AM=CN. Докажите, что MBND – параллелограмм.
В четырехугольнике ABCD ﮮA+ﮮB=180°, AB|| CD. На сторонах BC и AD отмечены точки M и K соответственно так, что BM=KD. Докажите, что точки M и K находятся на одинаковых расстояниях от точки пересечения диагоналей четырёхугольника.
На сторонах PK и MH параллелограмма MPKH взяты точки A и B соответственно, MP=PB=AK; ﮮMPB=60°. Найдите углы параллелограмма и сравните отрезки BM и AH.
На основании AC равнобедренного треугольника ABC отмечена точка K, а на сторонах AB и BC – точки M и P соответственно, причём PK=MB, ﮮKPC=80°, ﮮC=50°. Докажите, что KMBP – параллелограмм.
В четырехугольнике MPKH ﮮPMK=ﮮHKM, PK||MH. Через точку пересечения диагоналей проведена прямая, пересекающая стороны PK и MH в точках A и B соответственно. Докажите, что AP=HB.
На сторонах BC и AD параллелограмма ABCD взяты точки M и K, AB=BM=KD; ﮮAMB=30°. Найдите углы параллелограмма и сравните отрезки AM и CK.
В ΔMPK ﮮM=65°. На сторонах MK, MP, PK отмечены точки A, B, C соответственно так, что середина стороны PK – точка C, AM=KC, BP=AC, ﮮBAM=50°. Докажите, что BPCA – параллелограмм.
В выпуклом четырехугольнике ABCD ﮮA+ﮮB=ﮮB+ﮮC=180°. Через точку O пересечения диагоналей четырёхугольника проведена прямая, пересекающая стороны DC и AD в точках M и K соответственно; ﮮBOM=90°.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD отмечены точки M и H соответственно так, что отрезки BH и MD пересекаются в точке O; ﮮBHD=95°, ﮮDMC=90°, ﮮBOD=155°. Найдите отношение длин отрезков AB и MD и углы параллелограмма.
Точки M и K являются соответственно серединами сторон AB и BC треугольника ABC. Через вершину C вне треугольника проведена прямая, параллельная AB и пересекающая луч MK в точке E. Докажите, что KE=AC:2.
В выпуклом четырехугольнике MPKH ﮮM+ﮮP=180°, ﮮMKH=ﮮKMP. На сторонах MH и PK отмечены точки A и B так, что PB=PA. Отрезок AB проходит через точку пересечения диагоналей четырёхугольника. Докажите, что HP перпендикулярен AB.
Докажите, что BK=BM.
На сторонах BC и CD параллелограмма ABCD взяты точки K и M соответственно. Отрезки BM и KD пересекаются в точке O; ﮮBOD=140°, ﮮDKB=110°, ﮮBMC=90°. Найдите отношение длин отрезков MC и AD и углы параллелограмма.
Точки A и B принадлежат соответственно сторонам PE и ET треугольника PET. Прямая, проходящая через вершину T вне треугольника, пересекает луч AB и точке K так, что AP=KT, AB=BK=PT:2. Докажите, что точка A является серединой отрезка PE.
📹 Видео
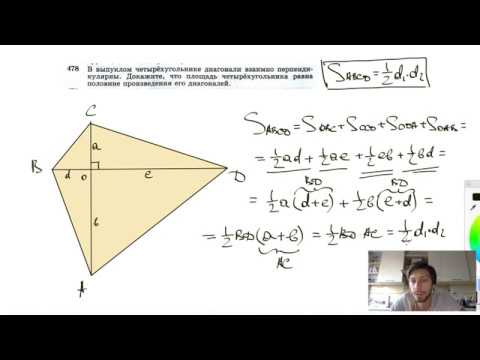
№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Открытая лекция «Описанная и вписанная окружность, решение задач»Скачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

10 класс, 26 урок, Многогранный уголСкачать

№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

№364. Найдите сумму углов выпуклого: а) пятиугольника; б) шестиугольника; в) десятиугольника.Скачать

КАК ИЗМЕРИТЬ УГЛЫ ЧЕТЫРЕХУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать



















