В треугольной пирамиде SABC известны боковые рёбра: SA = SB =13, Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 12.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
а) Пусть SH — высота пирамиды SABC. Треугольник ASB равнобедренный, поэтому прямые AB и SM перпендикулярны. Прямая AB перпендикулярна плоскости SMC, поскольку она перпендикулярна прямым SM и SH. Значит, CM является не только медианой, но и высотой треугольника ABC, то есть треугольник ABC равнобедренный.
б) В пирамиде SABC:
Значит, объём пирамиды
| Критерии оценивания выполнения задания | Баллы | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 | |||||||||||||||
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 | |||||||||||||||
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать  —>Решение задач и примеров —>—>
—> —> 23.08.2021 23.08.2021 26.04.2019 — Ссылки действительны в течение 24 часов до первой попытки скачать (90 минут с момента первого скачивания). 05.02.2019 — Ссылка на скачивание задач, приходит на указанный вами почтовый ящик при оформлении заказа и его оплаты. Дополнительная рассылка оплаченных заказов на E-mail производится в течение нескольких минут/часов, тема писем имеет вид «Заказ xxxxx». —> Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Задачи для самостоятельной работыДата добавления: 2015-08-06 ; просмотров: 2439 ; Нарушение авторских прав 1. По данным векторам а и b построить следующие их линейные комбинации: а) 2а + b; б) а — Зb; в) — а + 4-b; 2. Векторы 3. В треугольной пирамиде SABC известны векторы Найти вектор 4. Дана прямоугольная трапеция ABCD, длины оснований AD н ВС которой соответственно равны 4 и 2, а угол D равен 45°. Найти проекции векторов 5. Вектор а составляет с координатными осямн Ох и Оу углы 6. Найти длины диагоналей параллелограмма, построенного на векторах 7. Векторы 8.В параллелограмме ABCD даны стороны Выразить через 9. В Треугольнике ABC проведины меридианы a AK, BL и CM. Выразить 10. Даны векторы 11. Найти направляющие косинусы вектора 12.Дано 13. Найти угол А в треугольнике с вершинами A(1;2;-1), B(5;5;11), C(13;18;20) 14. Даны векторы 15. Даны векторы 16. Найти 17. Даны векторы 18.Даны три последовательные вершины параллелограмма А (-3;-2;0), В(3;-3;1) и С(5;0;2). Найти четвёртую вершину D и угол между векторами 19. Даны векторы 20. Найти площадь треугольника с вершинами А (2;2;2), В(1;3;3), С(3;4;2). 21. Упростить: 22. Известно, что 23. Найти площадь треугольника с вершинами в точках 24. Вычислить площадь треугольника с вершинами А (1;1;1), В (2;3;4), С (4;3;2). 25. Вычислить площадь и высоту параллелограмма, построенного на векторах 26. Найти площадь параллелограмма, построенного на векторах 27. Вычислить диагонали и площадь параллелограмма, построенного на векторах 28. Найти значения α и β, при которых векторы 29. На оси аппликат найти точку, равноудаленную от точек А(3;9;-1) и В(7;-3;9) 30. Определите координаты концов P и Q отрезка, который точками М(3;1;3) и N(6;-1;1) разделён на три части. 31. Проверить, является ли векторы 32. Найти объём тетраэдра с вершинами в точках А (-1;1;0), В(2;-2;1), С(3;1;-1), D(1;0;-2). 33. Вычислить объём параллелепипеда, построенного на векторах 34. Установить, лежат ли в одной плоскости точки А (4;3;10), В (5;1;5), С (2;2;5), D (3;4;12). 35. В тетраэдре с вершинами D (-3;-3;-3), A (2;-1;-3), B (-1;2;3) и C(-2;-2;1). Найти площадь грани АВС и длину высоты, проведённой к этой грани. 36.Выяснить, компланарны ли векторы 34. Определить 37. Найти объем тетраэдра с вершинами в точках А (-1; 1; 0 ), В ( 2; -2; 1 ), С (3; 1; -1 ), D =(1; 0; -2 ). 38. На прямой проходящей через точки А (-3;8;2) и B (1;-2;0) найти точку С, абсцисса которой 39. Найти объём треугольной пирамиды с вершинами в точках 40. Найти точку пересечения медиан треугольника, если вершинами его служат точки А(7;-4;5), В(-1;8;-2), С(-12;-1;6). 41. Найти все значения m, при которых вектор а(1; m; 3) линейно выражается через векторы b (2;3;7), c (3;-2;4), d (-1;1;-1). 42. Предприятие выпускает 4 вида продукции Р1, Р2; Р3, Р4 в количествах 50, 80, 20,120 единиц. При этом нормы расхода сырья составляют соответственно 7; 3,5; 10; 4 кг. Определите суммарный расход сырья и его изменение при изменениях выпуска продукции Р1, Р2; Р3, Р4 соответственно +5, -4, -2, +10 единиц. 43. Предприятие выпускает три вида продукции Р1, Р2; Р3 в количестве 15, 25, 40 штук, реализуемых по ценам 30, 40, 50 усл. Ед. соответственно. Найти выручку предприятия от реализации продукции и ее изменение при изменении Р1, Р2; Р3цен продукции соответственно на +5, -3, +2 усл. ед. 44. Выяснить, являются ли векторы а1=(4;-5;2;6),а2=(2;-2;1;3),а3=(6;-3;3;9),а4=(4; -1;5;6) линейно зависимыми? 3. Ответы: 4. 5. 6. 8. 9. 10 35. С(-2; 11/2; 3/2); 37. 25/6; 39.40/3; 40.(-2;1;3); 41. 1; 42. 1310 кг.; 41 кг.; 43. 3450 усл. ед.; 80 усл. ед. Вопросы для самопроверки и контроля 1. Понятие вектора. Линейные операции над векторами. 2. Длина вектора, равенство векторов. 3. Координаты вектора. 4. Проекция вектора на ось и на оси координат. Свойства проекции. 5. Линейная зависимость векторов. Базис. 6. Прямоугольный декартов базис. Разложение вектора по осям координат. 7. Направляющие косинусы. 8. Скалярное произведение векторов, его свойства. 9. Выражение скалярного произведения через координаты векторов 10. Условие перпендикулярности векторов. Нахождение угла между векторами. 11. Векторное произведение векторов, его свойства. 12. Выражение векторного произведения через координаты векторов. 13. Условие параллельности векторов. Нахождение площади треугольника (параллелограмма), построенного на векторах 14. Выражение векторного произведения через координаты векторов 15. Смешанное произведение векторов, его свойства. 16. Условие компланарности векторов. Нахождение объема параллелепипеда (пирамиды), построенного на векторах 17. Деление отрезка в данном отношении. 18. Аксиоматические построения и системы аксиом, n-мерный вектор и векторное пространство.
|
Не нашли то, что искали? Google вам в помощь!
🎦 Видео
Угол между векторами. 9 класс.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

2 37 Нахождение орта вектораСкачать

№767. Дан треугольник ABC. Выразите через векторы а=АВ и b=АС следующие векторы:Скачать

A.7.3 Проекции векторов. А вот и датасайнс!Скачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

Площадь треугольника, построенного на векторахСкачать

Задача 5. Компланарны ли векторы a, b, c.Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

§20 Нахождение объёма параллелипипедаСкачать

Урок 11. Решение задач на действия с векторамиСкачать

Задание 3 ЕГЭ профиль #121Скачать
Площадь параллелограмма по векторамСкачать

Самый сложный пример 5 задание проф. ЕГЭ (часть III)Скачать

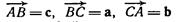 служат сторонами треугольника ABC. Выразить через а, b, с векторы
служат сторонами треугольника ABC. Выразить через а, b, с векторы 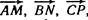 совпадающие с медианами треугольника.
совпадающие с медианами треугольника.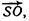 , если точка О является центром масс
, если точка О является центром масс 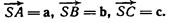 треугольника ABC.
треугольника ABC.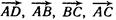 на ось
на ось 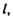 определяемую вектором
определяемую вектором 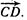 .
.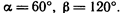 . Вычислить его координаты, если |а| =2.
. Вычислить его координаты, если |а| =2.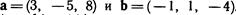
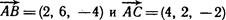 определяют стороны треугольника ABC. Найти длину вектора
определяют стороны треугольника ABC. Найти длину вектора 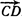 , совпадающего с медианой, проведенной из вершины С.
, совпадающего с медианой, проведенной из вершины С.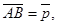
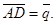
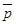 и
и 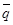 векторы
векторы 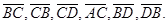
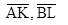 и
и 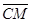 через векторы
через векторы 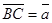 и
и 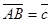 .
.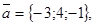
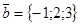 и
и 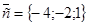 . Найти векторы:
. Найти векторы: 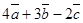 ;
; 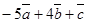 .
.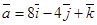
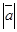 =5,
=5, 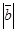 =6. Найти скалярное произведение векторов
=6. Найти скалярное произведение векторов  и
и 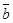 , если угол
, если угол 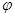 между ними равен 120°
между ними равен 120°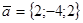 ,
, 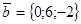 ,
, 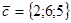 . Найти проекцию вектора
. Найти проекцию вектора 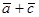 на вектор
на вектор 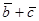 .
.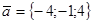 ,
, 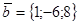 и
и 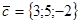 . Найти проекцию вектора
. Найти проекцию вектора 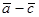 .
.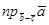 ,если
,если 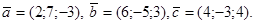
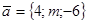 и
и 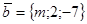 . При каком значении m эти векторы перпендикулярны?
. При каком значении m эти векторы перпендикулярны?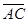 и
и 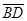 .
.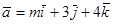 и
и 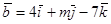 . При каком значении m векторы перпендикулярны?
. При каком значении m векторы перпендикулярны?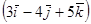
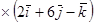
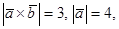 а угол между
а угол между 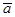 и
и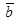 равен
равен 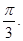 Найти
Найти 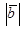 .
.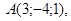
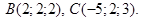
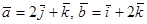
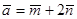 и
и 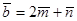 , где
, где 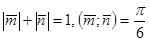 .
.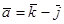 и
и 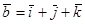 .
.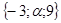 и
и 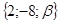 являются коллинеарными.
являются коллинеарными.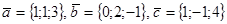 компланарными?
компланарными?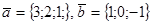 и
и 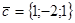 .
.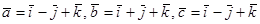 ?
?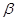 , при котором компланарны векторы
, при котором компланарны векторы 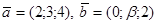 и
и 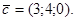
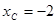
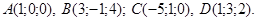
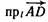
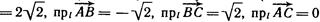 ,
,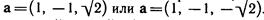
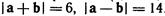 7.
7. 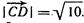
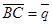 ,
, 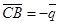 ,
, 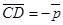 ,
, 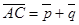 ,
, 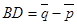
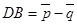 ;
;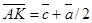 ,
, 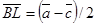 ,
, 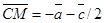 ;
;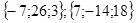 ; 11. cos
; 11. cos 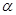 =8/9,cos
=8/9,cos 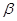 =-4/9,cos
=-4/9,cos 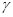 =1/9; 12. -15; 13.
=1/9; 12. -15; 13. 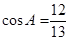 ; 14.
; 14. 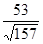 ; 15. 14/11; 16. -7/3; 17. -7; 18. D(-1;1;1)
; 15. 14/11; 16. -7/3; 17. -7; 18. D(-1;1;1) 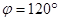 ; 19. 4; 20.
; 19. 4; 20. 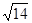 /2, 22.
/2, 22. 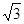 /2; 23.
/2; 23. 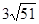 ; 24.
; 24. 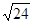 ; 25.
; 25. 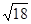
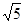 , 28. α=12; β=-6, 29. (0;0;12/5); 30. P(0;3;5) Q(9;-3;-1); 34. 1/6;
, 28. α=12; β=-6, 29. (0;0;12/5); 30. P(0;3;5) Q(9;-3;-1); 34. 1/6;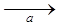 и
и 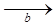 .
.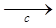 .
.