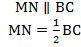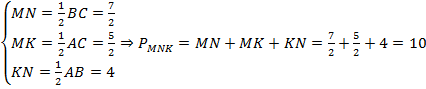В треугольнике авс проведена прямая параллельная основанию (6 видео)

В треугольнике abc проведена прямая, параллельная основанию ac и пересекающая стороны ab и bc в точках k и m соответственно?

Геометрия | 5 — 9 классы

В треугольнике abc проведена прямая, параллельная основанию ac и пересекающая стороны ab и bc в точках k и m соответственно.

Найдите периметр четырехугольника akmc, если известно, что bm = 2, мс = 6, cosC = 1 / 3 , km = 3.

Треугольник АВС, КМ параллельна АС, ВМ = 2, МС = 6, cosC = 1 / 3, КМ = 3

Треугольники КВМ и АВС подобны по трем углам угол В общий, угол ВКМ = углу ВАС как соответствующие, угол ВМК = углу ВСА как соответствующие = cosC = 1 / 3

ВМ / ВС = КМ / АС, 2 / 8 = 3 / АС АС = 12

КВ в квадрате = КМ в квадрате + ВМ в квадрате — 2 х КМ х ВМ хcosВМК = = 4 + 9 — 2 х 2 х 3 х 1 / 3 = 9

ВМ / МС = КВ / АК, 2 / 6 = 3 / АК, АК = 9

Периметр = 9 + 3 + 6 + 12 = 30.

Содержание

Помогите пожалуйста?
Через середину К медианы BM треугольника ABC и вершину А проведена прямая, пересекающая сторону ВС в точке P?
Через произвольную точку D, основания AC равнобедренного треугольника ABC проведены прямые , параллельные боковым сторонам треугольника и пересекающими их в точках M и M?
В равностороннем треугольнике ABC со стороной, равной 10 см, точки K и M — середины сторон AB и BC соответственно?
Через вершину b равнобедренного треугольника с основанием ac проведена прямая, параллельная биссектрисе cm этого треугольника и пересекающая прямую, содержащую сторону ac в точке k?
Медианы треугольника АВС пересекаются в точке О?
Медианы треугольника ABC пересекается в точке О?
В треугольнике ABC через точку пересечения медиан проведена прямая, Параллельная стороне AC и пересекающая стороны AB и BC в точках K и E соответственно?
Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O?
Медианы треугольника ABC пересекаются в точке O?
Как найти среднюю линию треугольника?
Понятие треугольника
Понятие средней линии треугольника
Понятие средней линии прямоугольного треугольника
Свойства средней линии треугольника
Теорема о средней линии треугольника
В треугольнике АВС = 12 см. Через точку пересечения медиан проведена прямая DE( D∈ АВ, Е ∈ ВС), параллельная АС. Найдите DE.
Ваш ответ
решение вопроса
Похожие вопросы

Видео:№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать

Помогите пожалуйста?

В треугольнике АВС проведена прямая, параллельная основанию АС и пересекающая стороны АВ и ВС в точках К и М соответственно.

Найдите периметр четырёхугольника АКМС, если известно, что ВМ = 2, МС = 6, cosC = 1 / 3, КМ = 3 С решением пожалуйста).

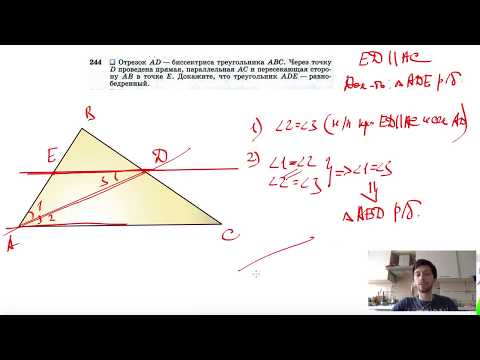
Видео:№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать

Через середину К медианы BM треугольника ABC и вершину А проведена прямая, пересекающая сторону ВС в точке P?

Через середину К медианы BM треугольника ABC и вершину А проведена прямая, пересекающая сторону ВС в точке P.

Найдите отношение площади треугольника ABC к площади четырехугольника KPCM.

Видео:№243. Через вершину С треугольника ABC проведена прямая, параллельная его биссектрисе АА1Скачать

Через произвольную точку D, основания AC равнобедренного треугольника ABC проведены прямые , параллельные боковым сторонам треугольника и пересекающими их в точках M и M?

Через произвольную точку D, основания AC равнобедренного треугольника ABC проведены прямые , параллельные боковым сторонам треугольника и пересекающими их в точках M и M.

Найти периметр BMDN, если AB = 10 см.

Видео:В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

В равностороннем треугольнике ABC со стороной, равной 10 см, точки K и M — середины сторон AB и BC соответственно?

В равностороннем треугольнике ABC со стороной, равной 10 см, точки K и M — середины сторон AB и BC соответственно.

A)Докажите, что AKMC — трапеция.

B)найдите периметр AKMC.

Видео:ОГЭ 23 КАК РЕШИТЬ ЗАДАЧУ НА ПОДОБНЫЕ ТРЕУГОЛЬНИКИСкачать

Через вершину b равнобедренного треугольника с основанием ac проведена прямая, параллельная биссектрисе cm этого треугольника и пересекающая прямую, содержащую сторону ac в точке k?

Через вершину b равнобедренного треугольника с основанием ac проведена прямая, параллельная биссектрисе cm этого треугольника и пересекающая прямую, содержащую сторону ac в точке k.

Найдите периметр треугольника abc, если ac = 2 м, ck = 4 м.

Видео:№245. Через точку пересечения биссектрис ВВ1 и СС1 треугольника ABC проведена прямая, параллельнаяСкачать

Медианы треугольника АВС пересекаются в точке О?

Медианы треугольника АВС пересекаются в точке О.

Через точку О проведена прямая, параллельная стороне АС и пересекающая АВ и ВС в точках Е и F соответственно, ЕF = 12.

Видео:Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

Медианы треугольника ABC пересекается в точке О?

Медианы треугольника ABC пересекается в точке О.

ЧЕрез точку О проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС соответственно.

Найдите EF, если сторона АС равна 15 см.

Видео:№473. Через вершину С треугольника ABC проведена прямая m, параллельная стороне АВ. Докажите,Скачать

В треугольнике ABC через точку пересечения медиан проведена прямая, Параллельная стороне AC и пересекающая стороны AB и BC в точках K и E соответственно?

В треугольнике ABC через точку пересечения медиан проведена прямая, Параллельная стороне AC и пересекающая стороны AB и BC в точках K и E соответственно.

Найдите AC, если KE = 12.

Найдите площадь треугольника BKE, если площадь треугольника ABC = 72см ^ 2 ( С решением пожалуйста).

Видео:№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать

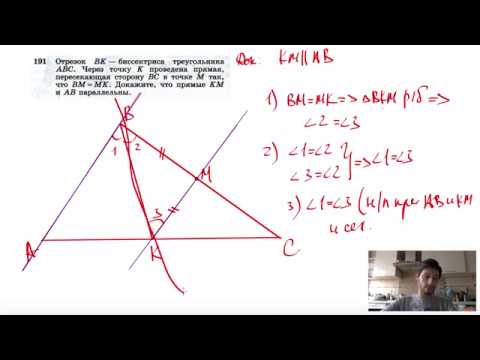
Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O?

Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O.

Через эту точку проведены прямые , параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно .

Докажите что периметр треугольника MOK равен длине стороны AC.

Видео:Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

Медианы треугольника ABC пересекаются в точке O?

Медианы треугольника ABC пересекаются в точке O.

Через точку O проведена прямая, параллельная стороне AC и пересекающая стороны AB и BC в точках E и F соответственно.

Найдите EF, если сторона AC = 15 см.

Перед вами страница с вопросом В треугольнике abc проведена прямая, параллельная основанию ac и пересекающая стороны ab и bc в точках k и m соответственно?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Дано : паралеллограмм авсd Ao = oc Po = oq Bp = qd Bd и ас — диагонали.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

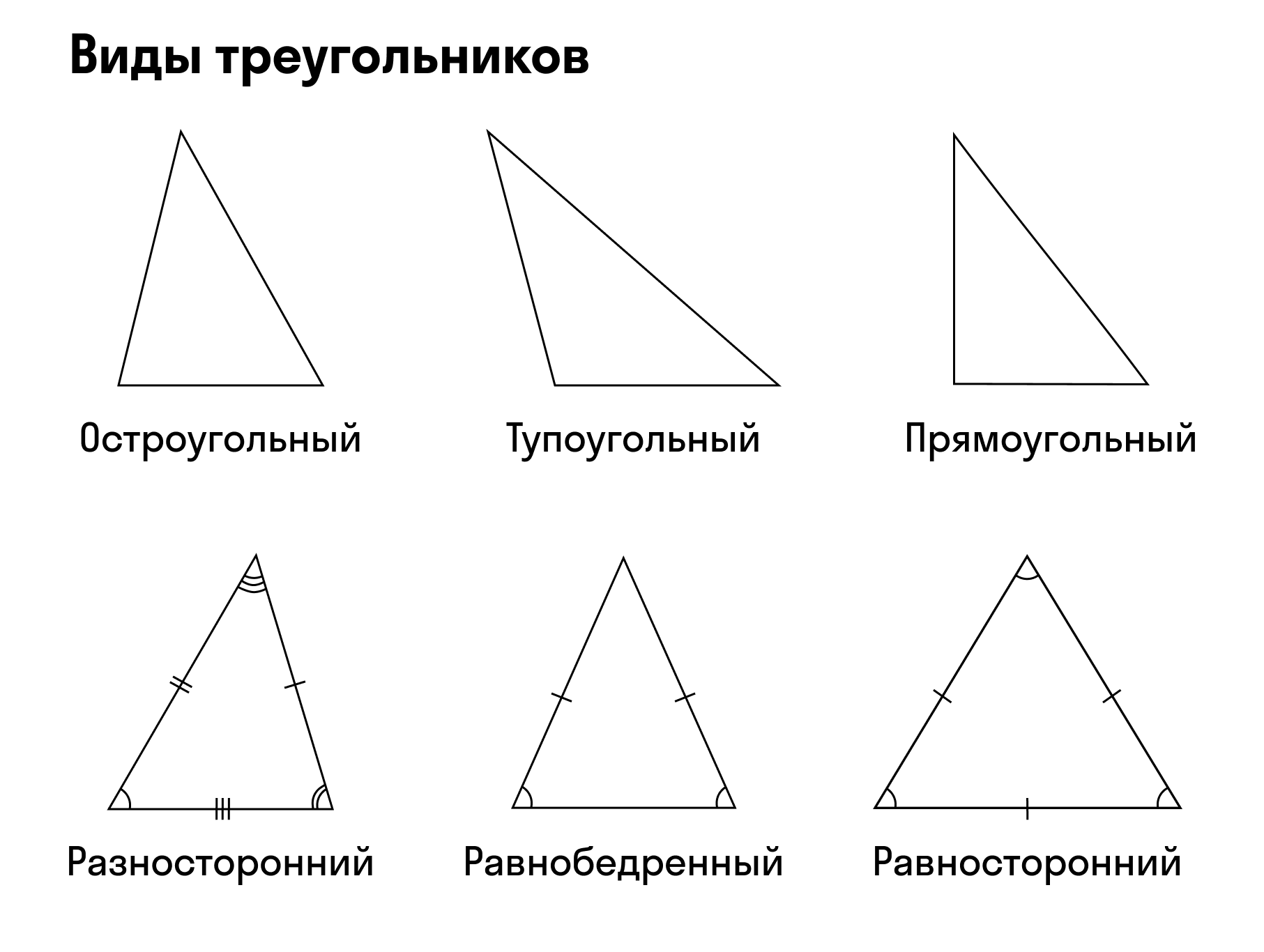
Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

В треугольнике против большего угла лежит большая сторона — и наоборот.
Сумма углов треугольника равна 180 градусов.
Все углы равностороннего треугольника равны 60 градусам.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:Задача по геометрии № 25 ОГЭ на отношение площадейСкачать

Понятие средней линии прямоугольного треугольника

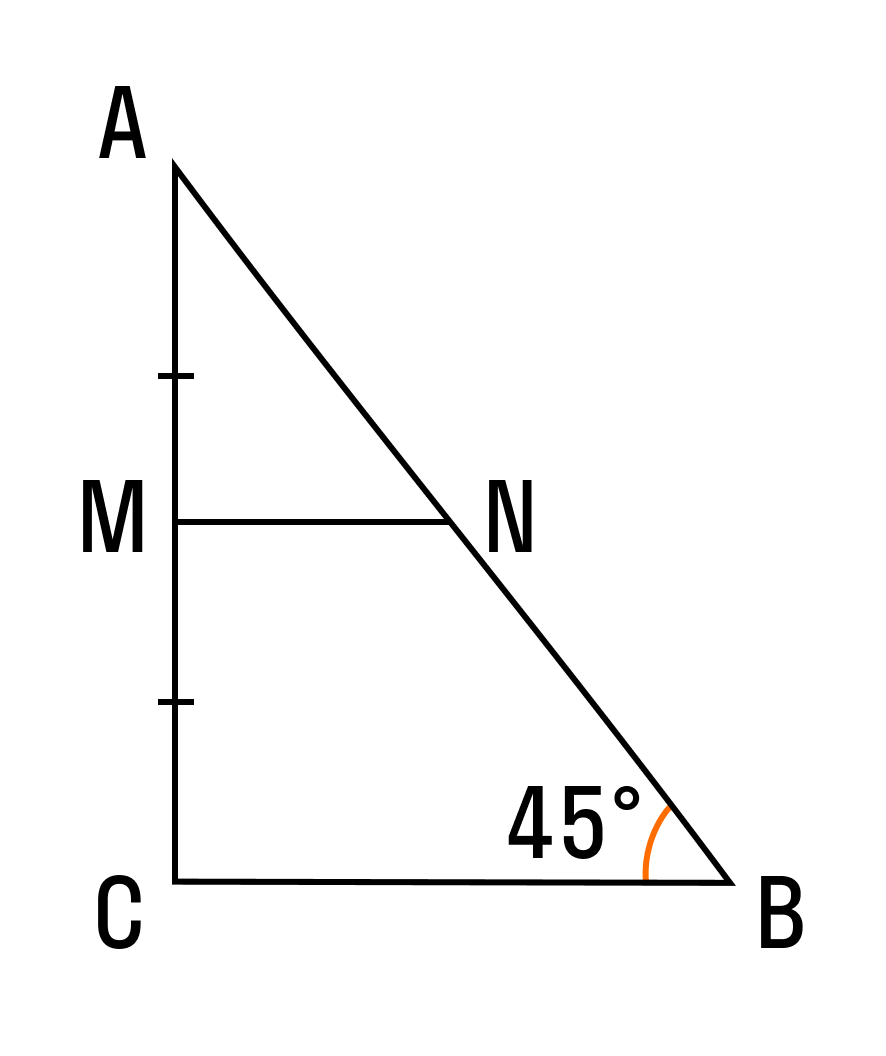
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые #математика #огэ #впрСкачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

Средняя линия равна половине длины основания и параллельна ему.
Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:№196. Дан треугольник ABC. Сколько прямых, параллельных стороне АВ, можно провестиСкачать

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

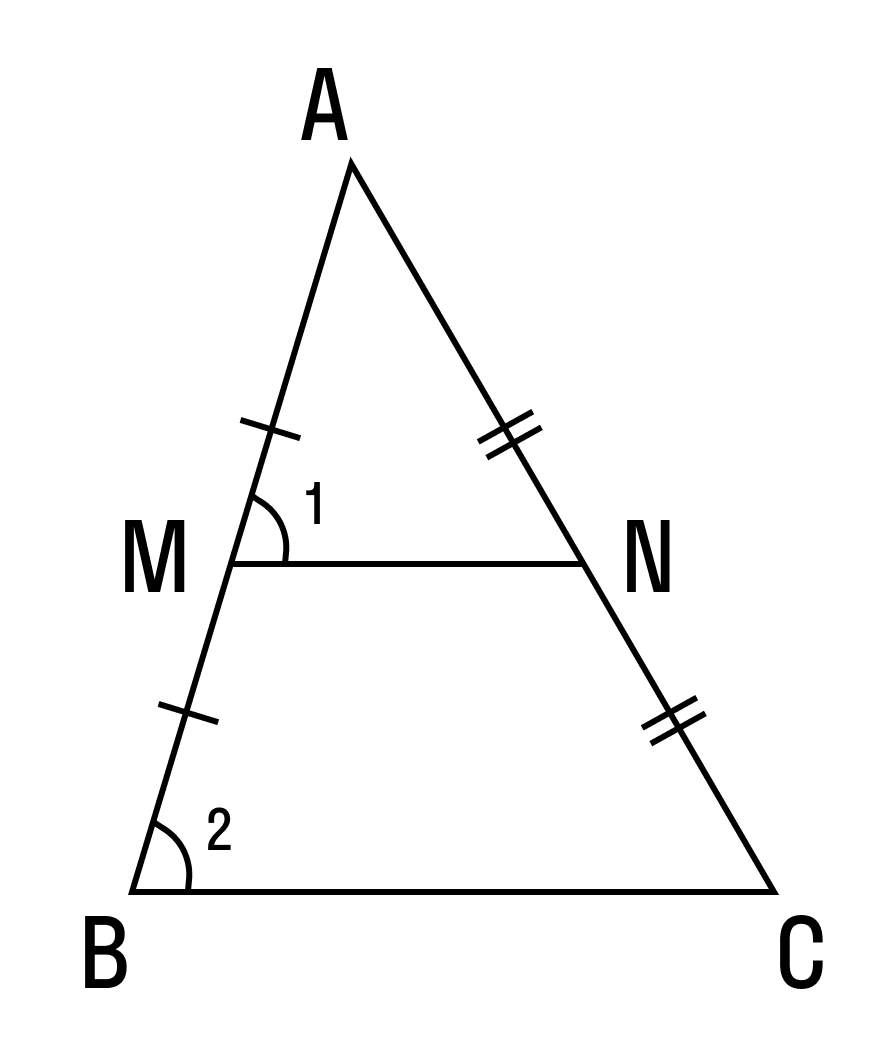
По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.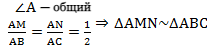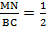

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

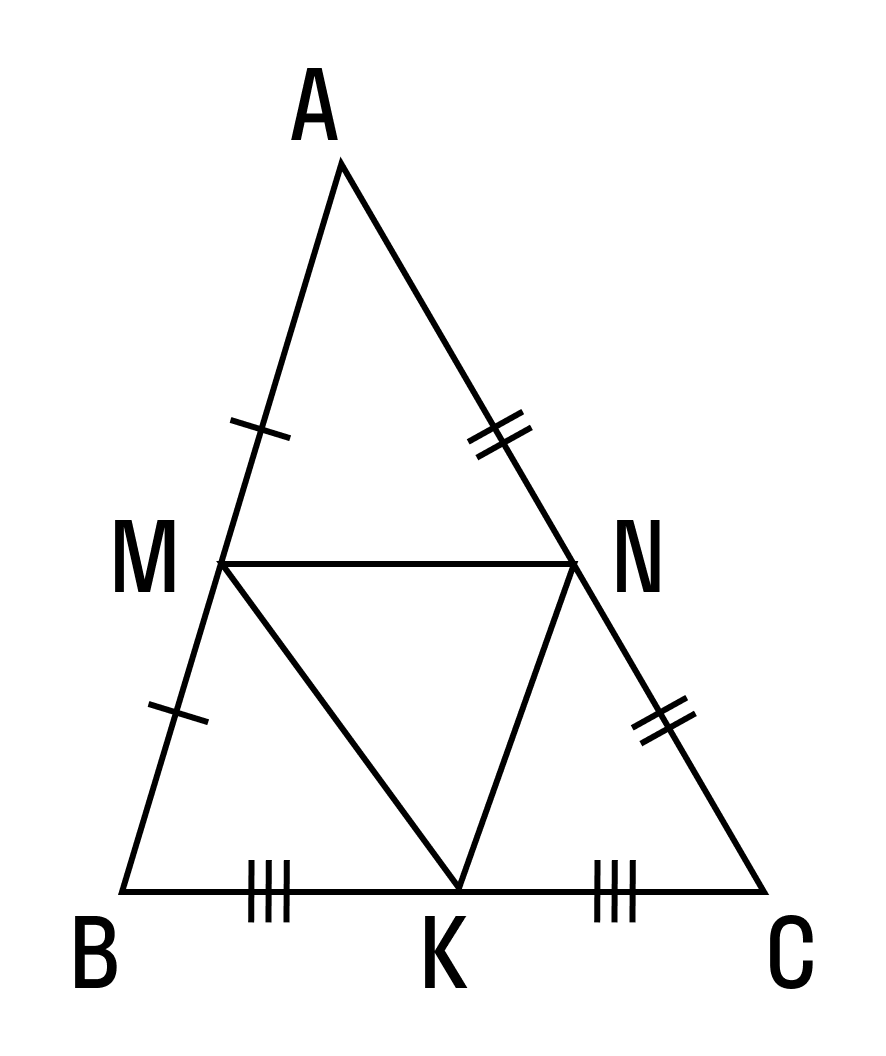
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

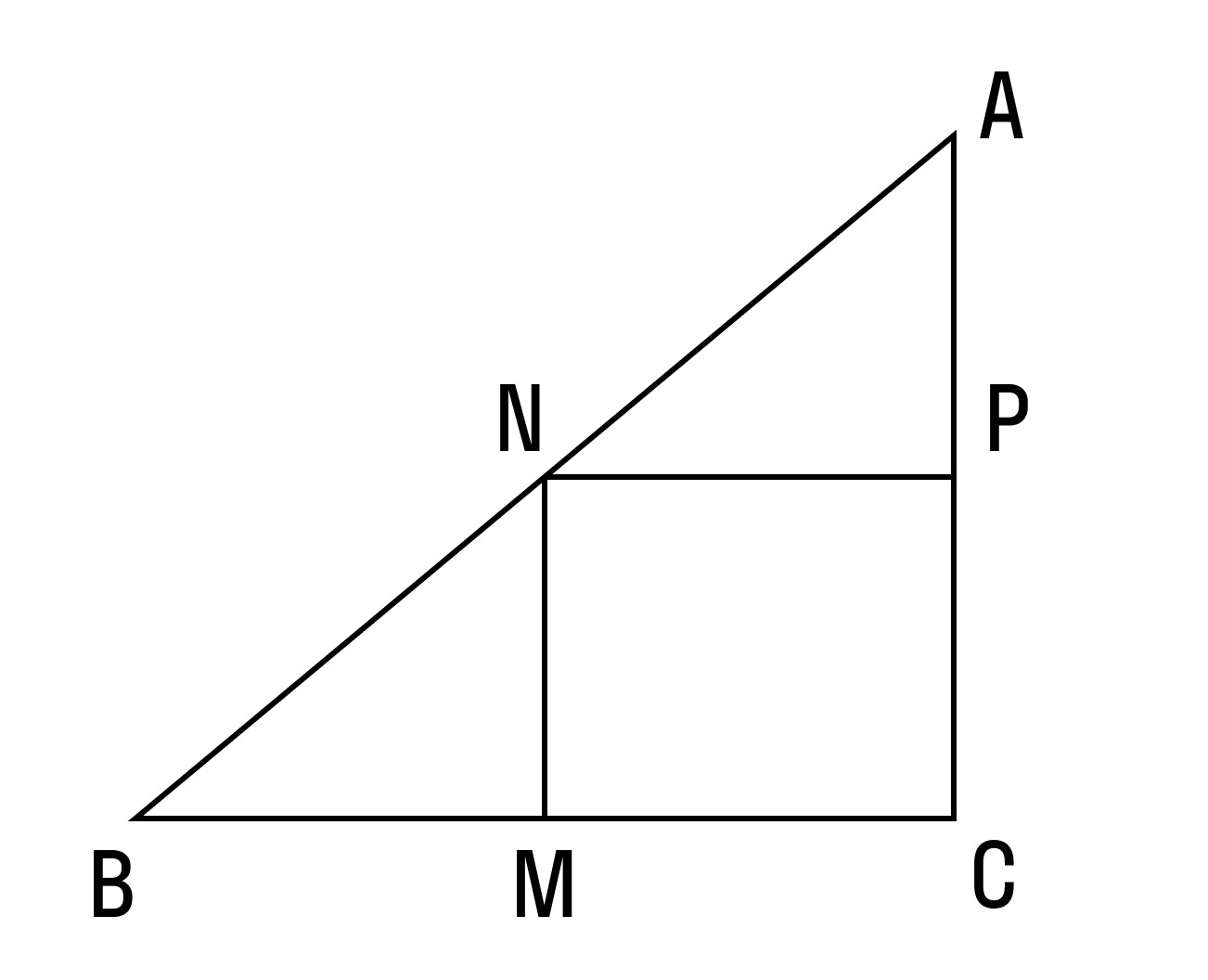
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

В треугольнике АВС = 12 см. Через точку пересечения медиан проведена прямая DE( D∈ АВ, Е ∈ ВС), параллельная АС. Найдите DE.

Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

Ваш ответ

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

решение вопроса

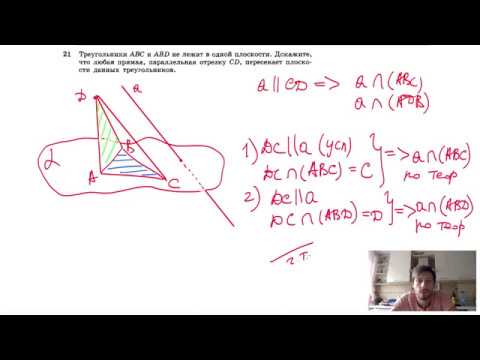
Видео:№21. Треугольники ABC и ABD не лежат в одной плоскости. Докажите,Скачать

В треугольнике авс проведена прямая параллельная основанию