Еще в Древнем Египте появилась наука, с помощью которой можно было измерять объемы, площади и другие величины. Толчком к этому послужило строительство пирамид. Оно предполагало значительное число сложных расчетов. И кроме строительства, было важно правильно измерить землю. Отсюда и появилась наука «геометрия» от греческих слов «геос» — земля и «метрио» — измеряю.
Исследованию геометрических форм способствовало наблюдение астрономических явлений. И уже в 17-м веке до н. э. были найдены начальные способы расчета площади круга, объема шара и главнейшее открытие — теорема Пифагора.

Формулировка теоремы об окружности, вписанной в треугольник выглядит следующим способом:
В треугольник можно вписать только одну окружность.
При таком расположении окружность — вписанная, а треугольник — описанный около окружности.
Формулировка теоремы о центре окружности, вписанной в треугольник, выглядит следующим образом:
Центральная точка окружности, вписанной в треугольник, есть точка пересечения биссектрис этого треугольника.
- Окружность, вписанная в равнобедренный треугольник
- Окружность, вписанная в прямоугольный треугольник
- Формулировка теоремы о вписанной окружности
- Теорема о центре окружности, вписанной в треугольник
- Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- В треугольник вписана окружность доказать что он прямоугольный
- 📺 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность, вписанная в равнобедренный треугольник
Окружность считается вписанной в треугольник, если она хотя бы одной точкой касается всех его сторон.
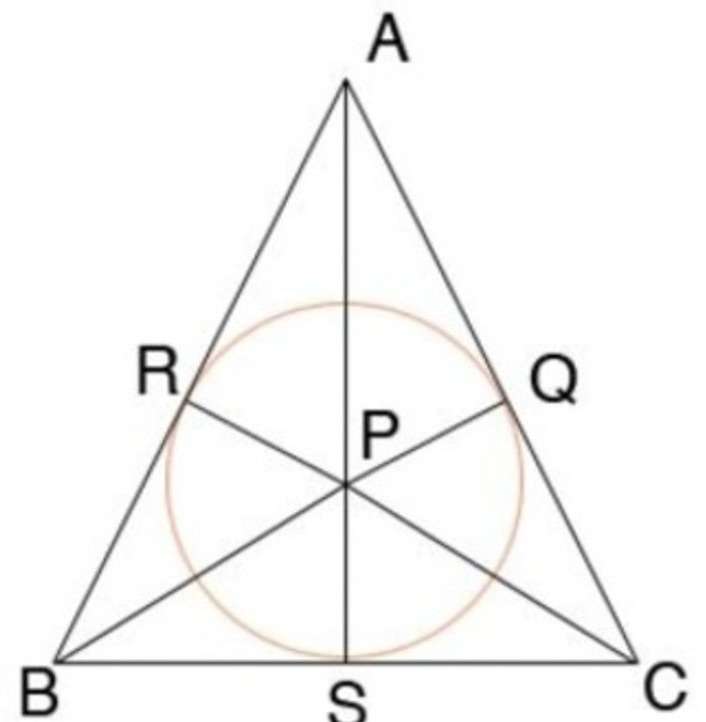
На фото ниже показана окружность, находящаяся внутри равнобедренного треугольника. Условие теоремы об окружности, вписанной в треугольник, соблюдено — она касается всех сторон треугольника AB, ВС И СА в точках R, S, Q соответственно.
Одним из свойств равнобедренного треугольника является то, что вписанная окружность точкой касания делит основание пополам (BS = SC), а радиус вписанной окружности составляет треть высоты данного треугольника(SP=AS/3).
Свойства теоремы об окружности, вписанной в треугольник:
- Отрезки, выходящие из одной вершины треугольника к точкам касания с окружностью, равны. На рисунке AR = AQ, BR = BS, CS = CQ.
- Радиус окружности (вписанной) — это площадь, деленная на полупериметр треугольника. Как пример, нужно начертить равнобедренный треугольник с теми же буквенными обозначениями, что на картинке, следующих размеров: основание ВС = 3 см, высота AS = 2 см, стороны АВ=ВС, соответственно, получаются по 2,5 см каждая. Проведем из каждого угла биссектрису и место их пересечения обозначим как Р. Впишем окружность с радиусом PS, длину которого нужно найти. Узнать площадь треугольника можно, умножив 1/2 основания на высоту: S = 1/2 * DC * AS = 1/2 * 3 * 2 = 3 см2. Полупериметр треугольника равен 1/2 суммы всех сторон: Р = (АВ + ВС + СА) / 2 = (2,5 + 3 + 2,5) / 2 = 4 см; PS = S/P = 3/4 = 0,75 см2, что полностью соответствует действительности, если измерить линейкой. Соответственно, верно свойство теоремы об окружности, вписанной в треугольник.
Видео:ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

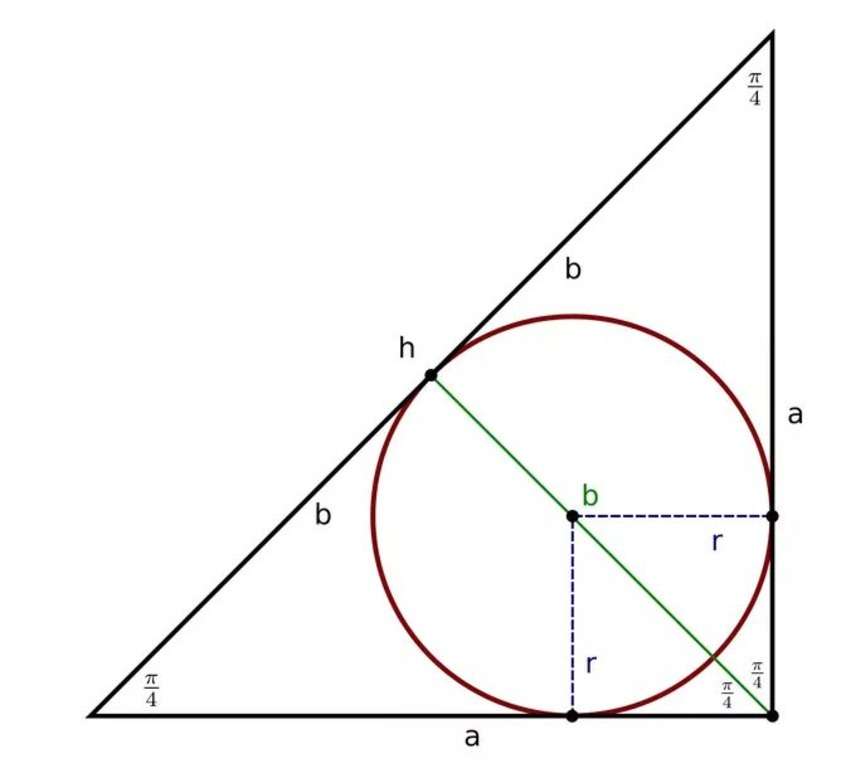
Окружность, вписанная в прямоугольный треугольник
Для треугольника с прямым углом действуют свойства теоремы об вписанной окружности в треугольник. И, кроме того, добавляется возможность решать задачи с постулатами теоремы Пифагора.
Радиус вписанной окружности в прямоугольный треугольник можно определить следующим образом: сложить длины катетов, вычесть значение гипотенузы и получившееся значение разделить на 2.
Есть хорошая формула, которая поможет высчитать площадь треугольника — периметр умножить на радиус вписанной в этот треугольник окружности.
Видео:Вписанный в окружность прямоугольный треугольник.Скачать

Формулировка теоремы о вписанной окружности
В планиметрии важны теоремы о вписанных и описанных фигурах. Одна из них звучит так:
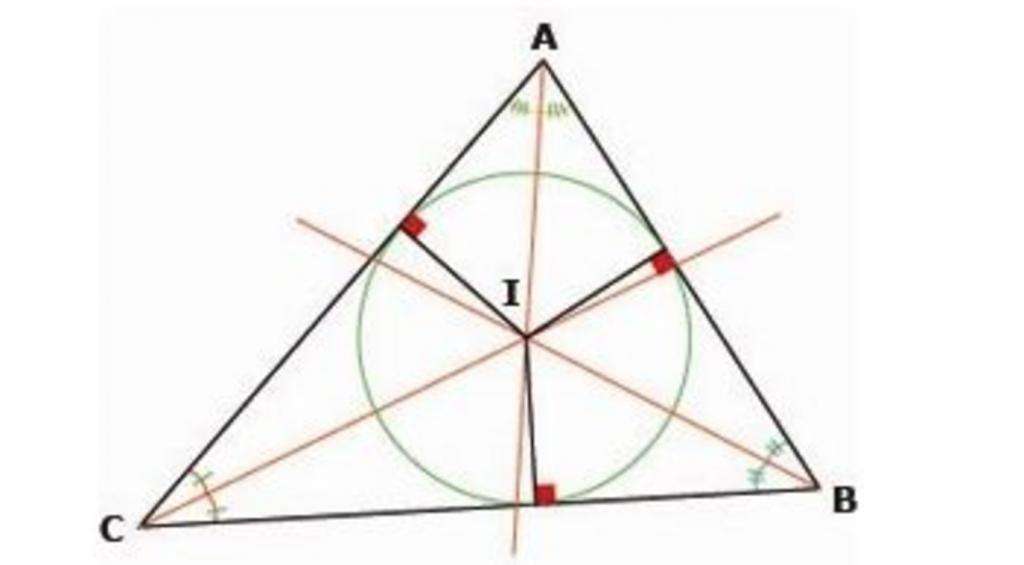
Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.
На представленном рисунке показано доказательство данной теоремы. Показано равенство углов, и, соответственно, равенство прилегающих треугольников.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Теорема о центре окружности, вписанной в треугольник
Радиусы окружности, вписанной в треугольник, проведенные в точки касания перпендикулярны сторонам треугольника.
Задание «сформулируйте теорему об окружности вписанной в треугольник» не должно застать врасплох, потому что это одни из фундаментальных и простейших знаний в геометрии, которыми необходимо владеть в полной мере для решения многих практических задач в реальной жизни.
Видео:Окружность, вписанная в прямоугольный треугольник | Геометрия 8-9 классыСкачать

Окружность, вписанная в треугольник. Основное свойство биссектрисы угла
 Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||||||||||||||
| Произвольный треугольник | ||||||||||||
 | ||||||||||||
| Равнобедренный треугольник | ||||||||||||
 | ||||||||||||
| Равносторонний треугольник | ||||||||||||
 | ||||||||||||
| Прямоугольный треугольник | ||||||||||||
 | ||||||||||||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Задание 25 Прямоугольный треугольник Вписанная окружностьСкачать
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
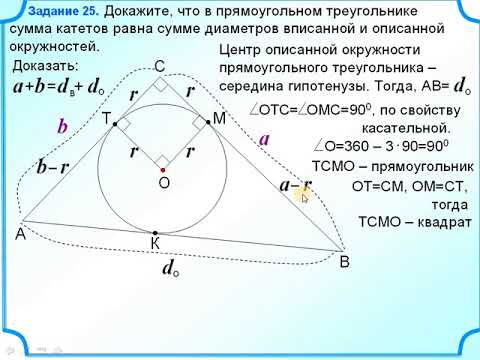
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
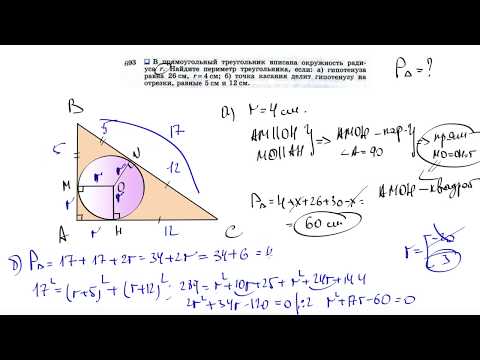
В треугольник вписана окружность доказать что он прямоугольный
В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке D, причём AD = R.
а) Докажите, что треугольник ABC прямоугольный.
б) Вписанная окружность касается сторон AB и BC в точках E и F. Найдите площадь треугольника BEF, если известно, что R = 2 и CD = 10.
а) Пусть O — центр вписанной окружности треугольника ABC.
Центр окружности, вписанной в угол, лежит на его биссектрисе, значит, AO — биссектриса угла BAC. Треугольник AOD прямоугольный и равнобедренный, поэтому ∠OAD = 45°. Следовательно, ∠BAC = 90°.
б) Обозначим BF = x. По теореме о равенстве отрезков касательных, проведённых к окружности из одной точки, AE = AD = 2, CF = CD = 10 и BE = BF = x. По теореме Пифагора BC 2 = AC 2 + AB 2 , или (10 + x) 2 = 12 2 + (2 + x) 2 . Из этого уравнения находим, что x = 3. Тогда
Ответ :
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше | 0 |
| Максимальный балл | 3 |
Аналоги к заданию № 502296: 502316 511378 Все
📺 Видео
Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Задание 24 Радиус окружности вписанной в прямоугольный треугольникСкачать
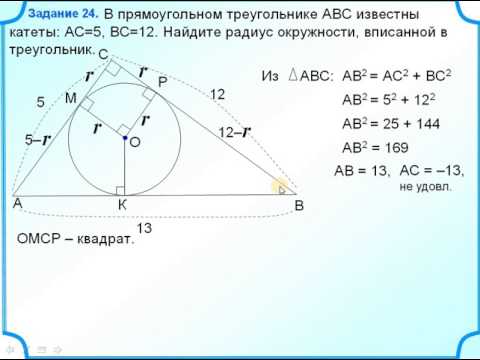
Задание 25 Прямоугольный треугольник Вписанная описанная окружностиСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Формулы для радиуса окружности #shortsСкачать

Тема 8. Прямоугольный треугольник и его описанная и вписанная окружностиСкачать

Прямоугольный треугольник и описанная окружностьСкачать