Рассмотрим далее основополагающие в линейной алгебре понятие о линейной зависимости и независимости векторов, а также определение базиса системы векторов.
Любую конечную последовательность векторов 




Система векторов 

Линейная зависимость и независимость есть свойства системы векторов. Однако часто соответствующие прилагательные относят и к самим векторам. Поэтому вместо «линейно независимая система векторов» допустимо говорить «линейно независимые векторы».
Например, двумерные арифметические векторы 






Если взять векторы 



Из определения линейной зависимости (независимости) системы векторов вытекают следующие утверждения.
1) Если некоторая система векторов содержит нулевой вектор, то она является линейно зависимой.
Пусть для определенности первый вектор системы является нулевым, т. е.
Тогда линейная комбинация векторов вида 
2) Если среди векторов системы есть такие, которые сами образуют линейно зависимую подсистему, то вся система также линейно зависима.
Так как исходная подсистема линейно зависима, то среди коэффициентов линейной комбинации векторов подсистемы имеется хотя бы один отличный от нуля. Добавим к этой линейной комбинацию линейную комбинацию векторов, не вошедших в исходную подсистему, с числовыми коэффициентами, равными нулю. Мы получим линейную комбинацию из векторов полной системы, которая равна нулевому вектору, причем имеется хотя бы один коэффициент отличный от нуля. Таким образом, наше утверждение доказано.
3) Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Если предположить обратное, т. е. существование некоторой линейно зависимой подсистемы, то по предыдущему утверждению отсюда следует зависимость исходной системы, что противоречит условию доказываемой теоремы. Полученное противоречие доказывает сформулированное утверждение.
4) Для того чтобы система из 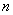
Необходимость. Пусть система векторов 

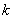

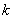


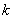




Достаточность. Пусть имеется некоторый вектор 


По аналогичной схеме доказывается следующее утверждение.
5) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов системы может быть представлен в виде линейной комбинации остальных векторов.
Видео:Линейно-независимая подсистема системы векторовСкачать

Как найти подсистему системы векторов
Определение 1. Система векторов 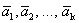
Определение 1´. Система векторов 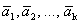
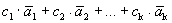
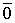
Покажем, что эти определения эквивалентны.
Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:
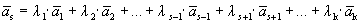
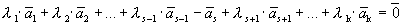
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна 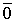
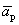
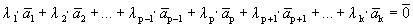
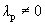
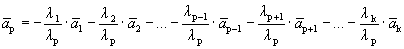
Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.
Определение 2. Единичным вектором, или ортом, 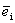
. 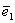
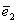
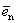
Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.
Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.
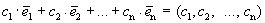
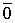
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.
Каждый вектор n -мерного пространства ā(а 1 , а 2 , . а n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора
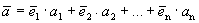
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.
Доказательство. Пусть дана система векторов 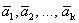
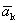
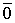
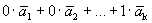
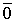
Следовательно, система линейно зависима.
Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.
Доказательство. Дана система векторов 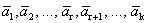
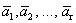
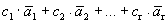
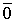
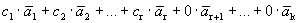
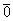
Получилось, что линейная комбинация векторов всей системы равна 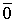
Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.
Теорема 4 (теорема Штейница). Если каждый из векторов 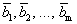
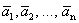
Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.
Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.
Видео:Линейная зависимость векторовСкачать

Как найти подсистему системы векторов
1.4. РАНГ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим систему векторов (1.1), где 
Теорема 1. 6. Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов.
Число векторов в максимальной линейно независимой подсистеме системы векторов (1.1) называется рангом последней. Системы векторов (1.1) и (1.2) называются эквивалентными, если векторы системы (1.1) линейно выражаются через систему векторов (1.2) и наоборот.
Теорема 1. 7. Ранги эквивалентных систем векторов равны.
Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:
1) изменение нумерации векторов в системе;
2) удаление нулевого вектора;
3) удаление вектора, являющегося линейной комбинацией остальных векторов системы;
4) умножение произвольного вектора системы на любое, не равное нулю число;
5) прибавление к одному из векторов системы линейной комбинации остальных векторов системы.
🔥 Видео
Образуют ли данные векторы базисСкачать

Линейная зависимость и линейная независимость векторов.Скачать

Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать

Найдите разложение вектора по векторам (базису)Скачать

Как разложить вектор по базису - bezbotvyСкачать

Линейная зависимость и линейная независимость. ТемаСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Линейная комбинация. Линейная зависимость (независимость) матриц.Скачать

Примеры линейной зависимости векторов.Скачать
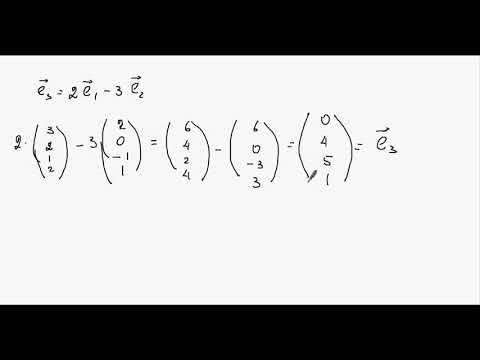
Собственные значения и собственные векторы матрицы (4)Скачать

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Решение "базисной системы векторов" (2)Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Разложение вектора по базису. 9 класс.Скачать

Линейная зависимость векторов на примерахСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

