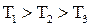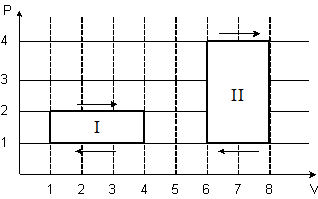- теория по физике 🧲 кинематика
- Период, частота и количество оборотов
- Линейная и угловая скорости
- Линейная скорость
- Угловая скорость
- Центростремительное ускорение
- Движение тела по окружности
- Материальная точка движется по окружности на чертеже изображена
- Кинематика поступательного движения
- ТЕСТОВЫЕ ЗАДАЧИ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ (с ответами)
- Движение по окружности с постоянной по модулю скоростью
- теория по физике 🧲 кинематика
- Период, частота и количество оборотов
- Линейная и угловая скорости
- Линейная скорость
- Угловая скорость
- Центростремительное ускорение
- 📹 Видео
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
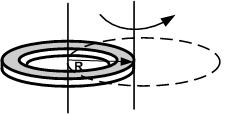
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
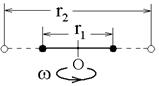
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Видео:Физика - движение по окружностиСкачать

Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Движение тела по окружности


как движение по отрезкам прямых и дугам окружностей,


В φ – угол поворота радиуса вектора
ω = 
показывающая угловое перемещение за единицу времени.
Линейная скорость – физическая величина, показывающая путь,
пройденный телом за единицу времени.
V = 
Период – время одного оборота. Т = 
Частота – число оборотов за единицу времени. ν = 
Связь линейной и угловой скорости: V = ω R;
При движении тела по окружности вектор перемещения направлен по хорде, вектор скорости – по касательной, а ускорение – к центру.





Тренировочные задания. Движение тела по окружности.
1(6-2006) Кубик массой 100г лежит без скольжения на вращающемся горизонтальном диске на расстоянии 50 см от оси вращения, при этом относительно модуль скорости кубика равен 2 м/с. Центростремительное ускорение кубика равно: 1) 12, 5м/с2; 2) 0,08м/с2; 3) 8м/с2; 4) 25м/с2;

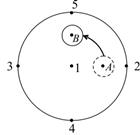
по окружности против часовой стрелки, через 3 с
первый раз попала из точки А в точку В.
Частота обращения точки равна …
1)



3.(ЕГЭ-07) Автомобиль движется с постоянной 1

представленной на рисунке. В какой из 2
указанных точек траектории центростремительное
ускорение максимально? 3
1) 1; 2) 2; 3) 3; 4) Во всех точках одинаково.
4.(1-07 ТР) Две материальные точки движутся по окружностям радиусами R1 и R2 = 2R1 с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением 1) Т1 = 0,5 Т2 ; 2) Т1 = Т2; 3) Т1 = 2Т2; 4) Т1 = 4Т1;
5.(Дем. Вар 07). Две материальные точки движутся по окружностям радиусами R1 и R2 = 2R1. При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением 1) а1 = 2 а2; 2) а1 = а2; 3) а1 = 0,5 а2; 4) а1 = 4 а2;
6.(62-06) Материальная точка движется по окружности. Как изменится величина ее центростремительного ускорения, если скорость увеличить в 2 раза, а радиус окружности в 2 раза уменьшить?
1) увеличится в 2 раза; 2) уменьшится в 2 раза; 3) увеличится в 4 раза; 4) уменьшится в 4 раза;
7.(254-05) Точка движется по окружности радиуса R со скоростью V. Как нужно изменить радиус окружности, сохранив скорость точки прежней, чтобы ее центростремительное ускорение при этом увеличилось вдвое? 1) увеличить в 2 раза; 2) увеличить в 4 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
8 (134-05) Самолет движется с постоянной по модулю скоростью по горизонтальной окружности. Как направлен вектор ускорения самолета при таком движении? 1) в плоскости окружности от ее центра. 2) в направлении вектора скорости. 3) противоположно вектору скорости.
4) в плоскости окружности к ее центру.
9. Материальная точка движется по окружности. Ее скорость увеличивают в 2 раза. Как нужно изменить радиус окружности, чтобы величина центростремительного ускорения точки не изменилась? 1) увеличить в 4 раза; 2) увеличить в 2 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
10. Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Центростремительное ускорение автомобиля равно 1) 1 м/с2; 2) 5 м/с2м/с2 4) 0,1 м/с2.
11. При равномерном движении тела по окружности остается постоянной6 1) линейная скорость. 2) угловая скорость. 3) период обращения. 4) частота обращения.
 |
12. Тело движется равномерно по окружности в направлении 2
против часовой стрелки. Какая стрелка (рис) указывает направление 2
вектора скорости при таком движении? 1
А)1; б) 2; в) 3; г) 4; д) 5; 5

против часовой стрелки. Какая стрелка (рис) указывает направление 2
вектора ускорения при таком движении? 1
А)1; б) 2; в) 3; г) 4; д) 5; 5
14. Автомобиль массой 1000 кг движется по выпуклому мосту радиус кривизны которого равен 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали состояние невесомости?1) 0,05 м/см/см/см/с
15.Чему равна линейная скорость верхней точки протектора колеса автомобиля относительно земли, если скорость движения автомобиля 15 м/с?
16. Тело совершает 50 оборотов за π секунд. На каком расстоянии от оси вращения находится точка, движущаяся со скоростью 10 м/с
1) 0,1 м; 2) 1 м; 3) 0,2π м; 4) 0,1π м







19. Шарик на стержне равномерно вращается в горизонтальной плоскости. На графике (рис. 42) представлена зависимость центростремительного ускорения шарика от его линейной скорости. Какова длина стержня? (Размеры шарика много меньше длины стержня.)
1) 1 м. 2)1,5 м. 3)З м. 4)9 м. 5)27м.
20. За 10 с точка прошла равномерно половину окружности, радиус которой 100 см. Определить линейную скорость.1)0,314м/с; 2) 0,1 м/с; 3)10 м/с; 4) 6,28 м/с;
21(136). Каков период вращения секундной, минутной и часовой стрелки часов? Какова частота вращения?
22(141). Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса локомотива, радиус которых 1,2 м?1)2,65 об; 2)159об; 3) 38,2об; 4)60 об.
23(144). Обтачиваемый на токарном станке вал диаметром 80 мм вращается с частотой 600 об/мин. Определить скорость резания.
24.(254) Точка движется по окружности радиуса R со скоростью V. Как нужно изменить радиус окружности, сохранив скорость точки прежней, чтобы ее центростремительное ускорение при этом увеличилось вдвое? 1) увеличить в 2 раза; 2) увеличить в 4 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
25 (134) Самолет движется с постоянной по модулю скоростью по горизонтальной окружности. Как направлен вектор ускорения самолета при таком движении? 1) в плоскости окружности от ее центра. 2) в направлении вектора скорости. 3) противоположно вектору скорости.
4) в плоскости окружности к ее центру.
26. Материальная точка движется по окружности. Ее скорость увеличивают в 2 раза. Как нужно изменить радиус окружности, чтобы величина центростремительного ускорения точки не изменилась? 1) увеличить в 4 раза; 2) увеличить в 2 раза; 3) уменьшить в 2 раза; 4) уменьшить в 4 раза;
27. Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Центростремительное ускорение автомобиля равно 1) 1 м/с2; 2) 5 м/с2м/с2 4) 0,1 м/с2.
150. Какова частота, и угловая скорость вращения колеса ветродвигателя, если за 2 мин (точно) колесо сделало 500 оборотов?
151. Во сколько раз угловая скорость минутной стрелки часов больше угловой скорости часовой стрелки?
152. На вал плотно насажены два шкива; диаметр первого 10 см, а второго 20см (сравнить угловые скорости шкивов.
154. Ветряное колесо радиусом 2,0 м делает 40,0 об/мин. Каково центростремительное ускорение концевых точек лопастей колеса? При какой частоте вращения центростремительное ускорение будет в 2 раза больше?
155. Какова линейная скорость тела, движущегося равномерно по окружности радиусом 3,0 м, если центростремительное ускорение равно 12 см/с2?
156. При постоянной скорости 900 км/ч самолет описывает вертикальную петлю. При каком радиусе петли центростремительное ускорение не превысит 5g?
157. Шкив вращается с угловой скоростью 50 рад/с. Определить центростремительные ускорения точек, находящихся на расстоянии 20 и 80 мм от оси вращения.
24(148). Определить угловые, скорости валов, Вращающихся с периодами Т1 = 10 с, Т2 = 0,050 с, Т3 = 1,00∙10 с.
25(149). Определить угловые скорости валов, частоты, вращения которых 24, 60, 1800 об/мин.
Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

Материальная точка движется по окружности на чертеже изображена
Видео:Почему бегут против часовой стрелки ?Скачать

Кинематика поступательного движения
Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?
 |
#1 #2 #3 #Во всех точках одинаково
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
# уменьшается # увеличивается # не изменяется
Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …
# уменьшается # увеличивается # не изменяется
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
# уменьшается # увеличивается # не изменяется
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
# увеличивается # уменьшается # не изменяется
Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения…
# увеличивается # уменьшается # не изменяется
Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения…
# уменьшается # увеличивается # не изменяется
Материальная точка M движется по окружности со скоростью 


Материальная точка M движется по окружности со скоростью 


Материальная точка M движется по окружности со скоростью 


Материальная точка M движется по окружности со скоростью 


Материальная точка M движется по окружности со скоростью 


Материальная точка M движется по окружности со скоростью 


Если at и an – тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения:
Если at и an – тангенциальная и нормальная составляющие ускорения, то соотношения: at = a = const, an = 0 справедливы для.
#прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного криволинейного движения #равномерного движения по окружности
Если at и an – тангенциальная и нормальная составляющие ускорения, то соотношения: at = 0, an = const справедливы для.
#равномерного криволинейного движения #прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного движения по окружности
Два тела брошены под одним и тем же углом к горизонту с начальными скоростями V0и 2V0. Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S2/S1 равно .
Материальная точка М движется по окружности со скоростью 




# 







Камень бросили под углом к горизонту соскоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Модуль тангенциального ускорения at на участке А-В-С…
# увеличится # не изменяется # уменьшается
Автомобиль движется с постоянной по величине скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории полное ускорение минимально?
 |
#1 #2 #3 #Во всех точках одинаково
Тело брошено с поверхности Земли со скоростью 20 м/с под углом 45° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).
#10 м #20 м #30 м #80 м
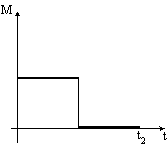
Графики зависимости величины тангенциального ускорения от времени для равномерного движения тела по окружности изображен на рисунке.
# 


Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости .
#равна нулю #меньше нуля #больше нуля
Материальная точка М движется по окружности со скоростью 




# 






Тело брошено с поверхности Земли со скоростью 20 м/с под углом 60° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).
#10 м #20 м #30 м #80 м
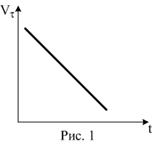
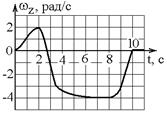
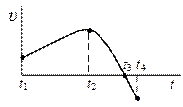
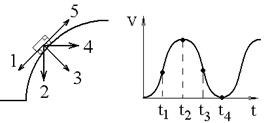
Материальная точка движется по окружности. На чертеже изображена зависимость ее скорости от времени. Точка имеет наибольшее тангенциальное ускорение в момент времени .
Тело брошено под углом к горизонту и движется в поле силы тяжести Земли. На рисунке изображен восходящий участок траектории данного тела.
Правильно изображает полное ускорение вектор .
Тело брошено с поверхности Земли со скоростью 20 м/с под углом 30° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).
#10 м #20 м #30 м #80 м
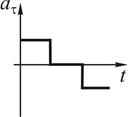
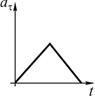
Тангенциальное ускорение точки меняется согласно графику.
Такому движению соответствует зависимость скорости от времени .
# 



Видео:Против часовой стрелкиСкачать

ТЕСТОВЫЕ ЗАДАЧИ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ (с ответами)
1. Если 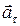
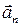
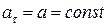
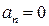
| !TRUE прямолинейного равноускоренного движения | !FALSE прямолинейного равномерного движения |
| !FALSE равномерного движения по окружности | !FALSE равномерного криволинейного движения |
2. Материальная точка А замедленно движется по дуге окружности со скоростью 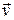
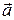
!TRUE 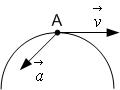 | !FALSE 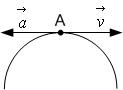 | !FALSE 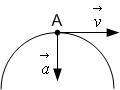 | !FALSE 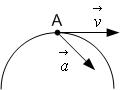 |
3. 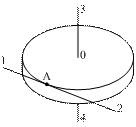
равноускоренно против часовой стрелки.
Вектор углового ускорения направлен вдоль линии …
| !True 3 | !False 2 | !False 4 | !False 1 |
7. Перечень контролируемых учебных элементов
Студент должен знать:
1) вектор скорости,
2) вектор ускорения,
3) составляющие ускорения – тангенциальное 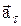
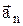
5) вектор углового перемещения,
6) вектор угловой скорости,
7) вектор углового ускорения;
4) устанавливать графическую интерпретацию зависимости величин, входящих в закон;
5) применять закон для анализа процессов на качественном уровне;
6) определять направление векторных величин;
8) анализировать информацию, представленную в виде графика, рисунка
9) применять закон для анализа процессов на расчетном уровне;
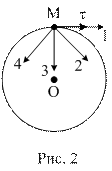
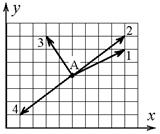
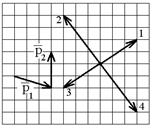
5. Материальная точка M движется по окружности со скоростью 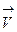
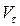
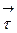
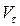
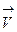
При этом вектор полного ускорения на рис.2 имеет направление …
| !True 4 | !False 1 | !False 2 | !False 3 |
6. Материальная точка движется по окружности. На чертеже изображена зависимость ее скорости от времени. Точка имеет наибольшее нормальное ускорение в момент времени …
| !TRUE t1 | !FALSE t2 | !FALSE t3 | !FALSE t4 |
7. Тангенциальное ускорение точки меняется согласно графику.
Такому движению соответствует зависимость скорости от времени …
!TRUE 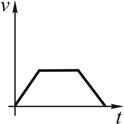 | !FALSE 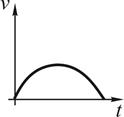 | !FALSE 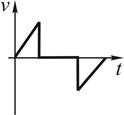 | !FALSE 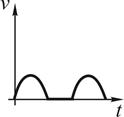 |
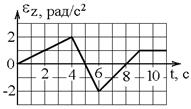
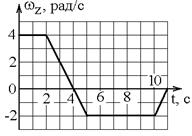
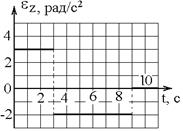
8. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике.
Тангенциальные ускорения точки на краю диска в моменты времени 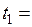
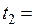
| !TRUE равны друг другу | !FALSE отличаются в 16 раз | !FALSE отличаются в 4 раза | !FALSE отличаются в 2,5 раза |
9. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции угловой скорости от времени показана на графике.
Нормальные ускорения точки на краю диска в моменты времени 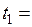
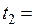
| !TRUE отличаются в 4 раза | !FALSE отличаются в 2 раза | !FALSE равны друг другу, но не равны нулю | !FALSE оба равны нулю |
10. Радиус-вектор частицы изменяется во времени по закону 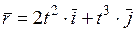
В момент времени 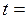
Скорость частицы в этот момент времени имеет направление …
| !TRUE 2 | !FALSE 1 | !FALSE 3 | !FALSE 4 |
11. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике.
Через 11 с тело окажется повернутым относительно начального положения на угол (рад) …
12. Тангенциальное ускорение точки меняется согласно графику.
Такому движению соответствует зависимость скорости от времени …
!TRUE 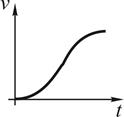 | !FALSE 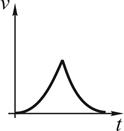 | !FALSE 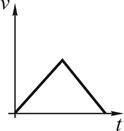 | !FALSE 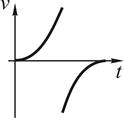 |
12. Материальная точка движется по окружности. На чертеже изображена зависимость ее скорости от времени. Точка имеет только нормальное ускорение в момент времени …
| !TRUE t2 | !FALSE t1 | !FALSE t3 | !FALSE t4 |
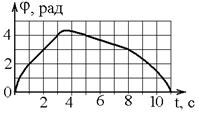
13. Легкий диск радиуса R начинает вращаться в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость угла поворота от времени показана на графике.
Величины нормальных ускорений точки на краю диска в моменты времени 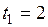
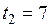
| !TRUE отличаются в 9 раз | !FALSE отличаются в 3 раза | !FALSE отличаются примерно в 1,1 раза | !FALSE равны нулю |
14. В начальный момент времени 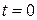
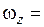
Нормальное ускорение некоторой точки этого тела через 5 с после начала вращения …
| !TRUE увеличится в 4 раза | !FALSE увеличится в 2 раза | !FALSE увеличится в 1,5 раза | !FALSE не изменится |
15. На тело, брошенное под углом к горизонту, во время полета действует горизонтальная сила. Сопротивлением воздуха пренебречь. От величины этой силы зависит…
| !True дальность полета | !False высота подъема | !False время полета |
16. Вес тела массой m в лифте, поднимающемся вверх с ускорением 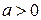
!TRUE 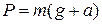 | !FALSE 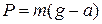 | !FALSE 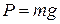 | !FALSE 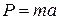 |
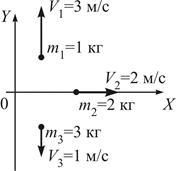
17. Система состоит из трех шаров c массами 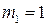
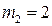
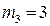
Если скорости шаров равны 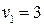
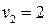
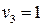
!True 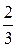 | !False 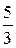 | !False 4 | !False 10 |
18. В момент времени t1 автомобиль поднимался по участку дуги.
Направление результирующей всех сил, действующих на автомобиль в этот момент времени правильно отображает вектор …
| !TRUE 4 | !FALSE 1 | !FALSE 2 | !FALSE 3 | !FALSE 5 |
19. Импульс тела 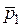
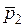
В момент удара сила действовала в направлении …
| !TRUE 2 | !FALSE 1 | !FALSE 3 | !FALSE 4 |
20. На материальную точку действует сила 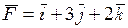
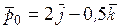
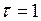
!True 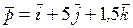 | !False 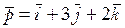 | !False 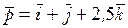 | !False 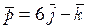 |
21. Теннисный мяч летел с импульсом 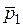
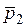
Сила действовала на мяч в течении …
| !TRUE 0,1 с | !FALSE 0,01 с | !FALSE 0,05 с | !FALSE 0,5 с |
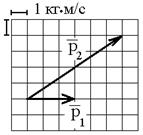
22. Направления векторов момента импульса 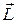
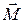
!TRUE 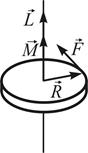 | !FALSE 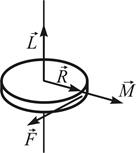 | !FALSE 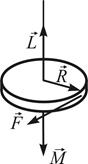 | !FALSE 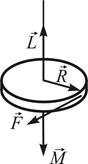 | !FALSE 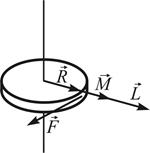 |
23. Алюминиевый и стальной цилиндры имеют одинаковую высоту и равные массы. Относительно моментов инерции этих цилиндров справедливо следующее суждение:
| !TRUE момент инерции алюминиевого цилиндра больше момента инерции стального цилиндра | !FALSE момент инерции стального цилиндра больше момента инерции алюминиевого цилиндра | !FALSE моменты инерции цилиндров равны |
24. Абсолютно твердое тело вращается с угловым ускорением, изменяющимся по закону 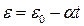
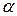
!True 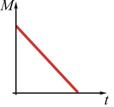 | !False 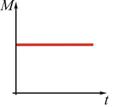 | !False  | !False 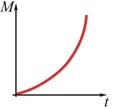 | !False 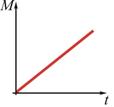 |
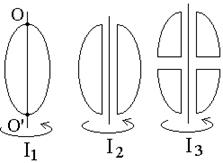
25. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну — пополам вдоль оси симметрии, а вторую — на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO’.
Для моментов инерции относительно оси OO’ справедливо соотношение …
!TRUE 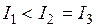 | !FALSE 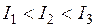 | !FALSE 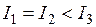 | !FALSE 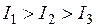 |
26. При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера.
Если ось вращения тонкого кольца перенести из центра масс на край, то момент инерции относительно новой оси увеличится в….
| !True 2 раза | !False 3 раза | !False 4 раза | !False 1.5 раза |
27. Диск вращается равномерно с некоторой угловой скоростью 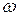
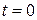
График, правильно отражающий зависимость угловой скорости диска от времени, представлен на рисунке …
!TRUE  | !FALSE  | !FALSE  | !FALSE  |
28. В однородном диске сделано круглое отверстие с центром в точке А и вынутый цилиндр положен так, что его ось проходит через точку В. Цифрами 1, 2, 3, 4, 5 обозначены оси, перпендикулярные поверхности диска.
В результате такого перемещения вещества суммарный момент инерции диска и цилиндра увеличится относительно осей …
| !TRUE 2, 4 | !FALSE 3, 5 | !FALSE 1, 3 | !FALSE 1, 5 |
29. Физический маятник совершает колебания вокруг оси, проходящей через точку О и перпендикулярной плоскости рисунка.
Для данного положения маятника момент силы тяжести относительно т.О направлен…
| !True перпендикулярно плоскости рисунка к нам | !False перпендикулярно плоскости рисунка от нас | !False в плоскости рисунка вниз | !False в плоскости рисунка вверх |
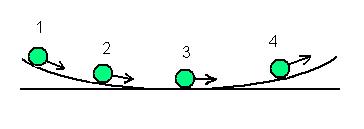
30. Шарик скатывается по желобу, изогнутому в виде дуги окружности. Стрелкой указано направление линейной скорости центра масс шарика. Для положения 4 правильно указаны следующие направления углового ускорения и момента внешних сил…
| !True угловое ускорение и момент сил направлены к нам перпендикулярно плоскости рисунка | !False угловое ускорение направлено к нам, а момент сил направлен от нас перпендикулярно плоскости рисунка | !False угловое ускорение и момент сил направлены от нас перпендикулярно плоскости рисунка | !False угловое ускорение и момент сил совпадают с направлением скорости |
31. Шар массы 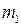
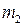
| !True первый шар остановится, а второй будет двигаться в том же направлении | !False оба шара будут продолжать движение в том же направлении | !False после удара оба шара придут в движение с одинаковыми скоростями | !False первый шар полетит после удара в обратном направлении, покоящийся шар придет в движение |
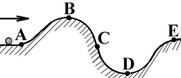
32. Шарику в точке А была сообщена начальная кинетическая энергия достаточная для прохождения в поле силы тяжести без трения через подъем и впадину.
На рисунке шарик имеет наибольшую кинетическую энергию в точке …
| !True D | !False B | !False C | !False E |
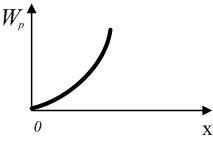
33. В потенциальном поле сила 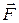
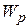
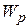
то зависимость проекции силы 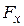
!True 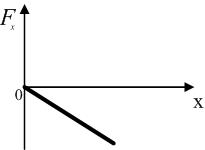 | !False 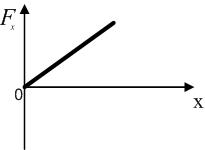 | !False  | !False  |
34. Тело массой m начинает двигаться под действием силы 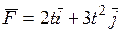
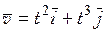
!True 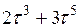 | !False 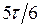 | !False 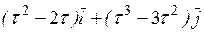 | !False 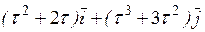 |
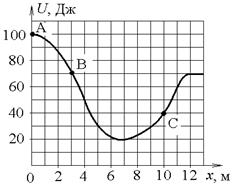
35. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике 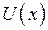
Кинетическая энергия шайбы в точке С …
| !TRUE в 2 раза больше, чем в точке В | !FALSE в 2 раза меньше, чем в точке В | !FALSE в 1,75 раза больше, чем в точке В | !FALSE в 1,75 раза меньше, чем в точке В |
36. Если зависимость работы, совершаемой силой 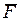
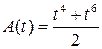
!True 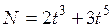 | !False 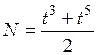 | !False 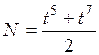 | !False 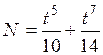 |
37. 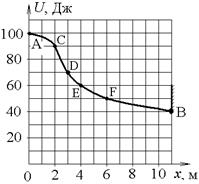
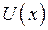
Шайба остановится в точке .
| !TRUE D | !FALSE C | !FALSE E | !FALSE F |
38. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости тел одинаковы, то…
| !TRUE выше поднимется полый цилиндр | !FALSE выше поднимется сплошной цилиндр | !FALSE оба тела поднимутся на одну и ту же высоту |
39. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости 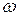
При этом была совершена работа …
!TRUE 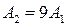 | !FALSE 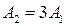 | !FALSE 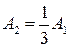 | !FALSE 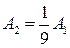 |
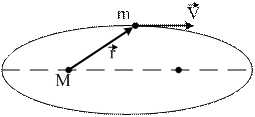
40. Планета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массой М.
Если 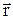
| !True Момент импульса планеты относительно центра звезды при движении по орбите не изменяется | !False Момент силы тяготения, действующей на планету, относительно центра звезды, не равен нулю | !False Для момента импульса планеты относительно центра звезды справедливо выражение: 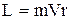 |
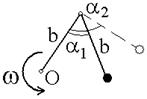
41. Два невесомых стержня длины b соединены под углом a1=60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью 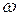
Система стала вращаться с угловой скоростью …
!TRUE 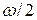 | !FALSE 2 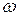 | !FALSE 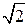 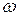 | !FALSE 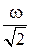 |
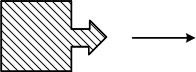
42. На борту космического корабля нанесена эмблема в виде геометрической фигуры.
Из-за релятивистского сокращения длины эта фигура изменяет свою форму. Если корабль движется в направлении, указанном на рисунке стрелкой, со скоростью, сравнимой со скоростью света, то в неподвижной системе отсчета эмблема примет форму, указанную на рисунке …
!TRUE 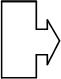 | !FALSE  | !FALSE  |
43. Предмет движется со скоростью 0,6с (с – скорость света в вакууме) относительно неподвижной системы отсчета. Тогда его длина .
| !True уменьшается на 20 % | !False увеличивается на 20 % | !False уменьшается на 10 % | !False увеличивается на 10 % |
44. При движении частицы по кривой со скоростью, близкой к скорости света, правильные направления ее полного ускорения 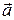
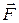
!TRUE 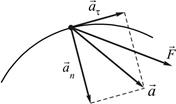 | !FALSE 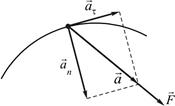 | !FALSE 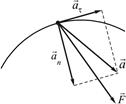 |
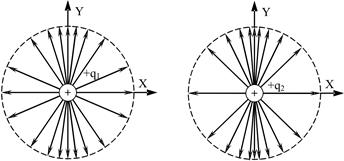
45. На рисунках изображены силовые линии электрических полей, созданных положительными зарядами q1 и q2.
| !TRUE равномерно движутся вдоль оси Х, причем q2 быстрее, чем q1 | !FALSE равномерно движутся вдоль оси Х, причем q2 медленнее, чем q1 | !FALSE равномерно движутся вдоль оси Y, причем q2 медленнее, чем q1 | !FALSE равномерно движутся вдоль оси Y, причем q2 быстрее, чем q1 |
ТЕРМОДИНАМИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА
1. Состояние идеального газа определяется значениями параметров: 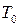
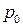
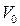
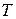
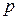
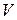
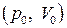
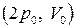
| !TRUE увеличилась | !FALSE уменьшилась | !FALSE не изменилась |
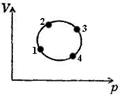
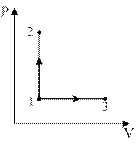
2. На рисунке изображен цикл для постоянной массы газа в координатах 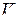
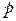
Из указанных на графике четырёх точек наибольшей температуре соответствует точка…
| !True 3 | !False 1 | !False 2 | !False 4 |
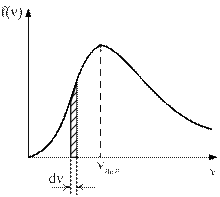
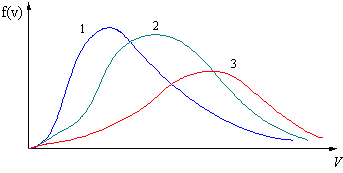
3. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 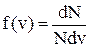
Для этой функции верным утверждением является…
| !TRUE с ростом температуры максимум кривой смещается вправо | !FALSE с ростом температуры площадь под кривой растет | !FALSE с ростом температуры величина максимума растет |
4. В трех одинаковых сосудах находится одинаковое количество газа, причем
Распределение скоростей молекул в сосуде с температурой Т3 будет описывать кривая.
| !True 1 | !False 2 | !False 3 |
5. В сосуде, разделенном на равные части неподвижной теплоизолирующей перегородкой, находится одинаковое количество идеального газа, причем давление Р1>P2 .
Распределение молекул газа по скоростям для обеих частей сосуда правильно указано на рисунке.
!True 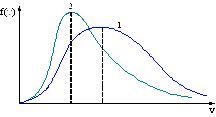 | !False 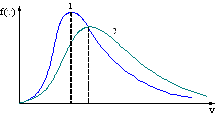 | !False 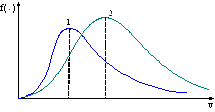 |
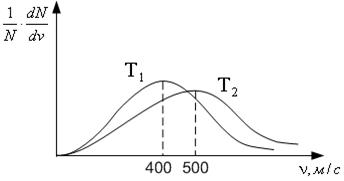
6. На рисунке приведены две кривые распределение молекул одного газа по абсолютным скоростям при разных значениях температур. Отношение температур 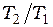
| !True 25/16 | !False 16/25 | !False 5/4 | !False 4/5 |
15. Средняя кинетическая энергия молекулы идеального газа при температуре T равна 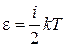
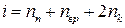
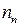
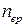
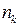
| !TRUE 3 | !FALSE 1 | !FALSE 5 | !FALSE 7 |
16. На каждую степень свободы движения молекулы приходится одинаковая энергия, равная 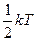
!True 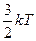 | !False 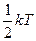 | !False 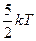 | !False 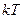 |
17. Теплоемкость произвольного количества идеального газа при изотермическом процессе равна …
| !TRUE ∞ | !FALSE 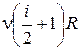 | !FALSE 0 | !FALSE 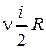 |
18. Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
Тогда 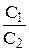
!TRUE 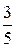 | !FALSE 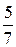 | !FALSE 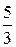 | !FALSE 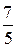 |
19. Давление газа, находящегося в закрытом сосуде при некоторой температуре, можно рассчитать и как для идеального газа 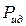
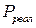
TRUE всегда 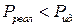 | !FALSE всегда 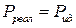 | !FALSE всегда 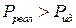 | !FALSE отношение давлений зависит от температуры и концентрации молекул |
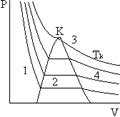
20. На рисунке представлен набор экспериментальных изотерм реального газа.
Область, в которой пар находится в динамическом равновесии с жидкостью, обозначена цифрой …
| !TRUE 2 | !FALSE 1 | !FALSE 3 | !FALSE 4 |
21. Если 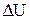
!TRUE 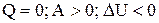 | !FALSE 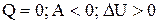 | !FALSE 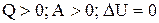 | !FALSE 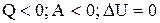 |
22. Работа, совершаемая идеальным газом при его изотермическом расширении, численно равна заштрихованной площади, показанной на рисунке …
!TRUE 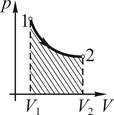 | !FALSE 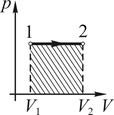 | !FALSE 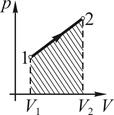 | !FALSE 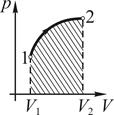 |
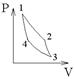
23. На (P,V)-диаграмме изображены два циклических процесса.
Отношение работ АI/АII, совершенных в этих циклах, равно…
| !TRUE ½ | !FALSE 2 | !FALSE -1/2 | !FALSE -2 |
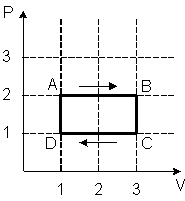
24 .На (P,V)-диаграмме изображен циклический процесс.
На участках BC и CD температура …
| !TRUE понижается | !FALSE на BC – понижается, на CD – повышается | !FALSE на BC – повышается, на CD – понижается | !FALSE повышается |
25. Газ находится в состоянии с параметрами р1, V1. Необходимо расширить газ, затратив при этом минимум энергии. Для этого подходит процесс…
| !True адиабатический | !False изотермический | !False изохорический | !False изобарический |
26. Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла…
| !TRUE увеличится | !FALSE уменьшится | !FALSE не изменится |
27. Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1).
В процессе изотермического расширения 1-2 энтропия рабочего тела …
| !TRUE возрастет | !FALSE не изменится | !FALSE уменьшится |
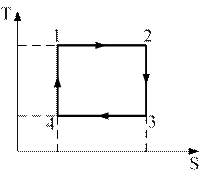
28. На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Теплота подводится к системе на участке …
| !TRUE 1 – 2 | !FALSE 2 – 3 | !FALSE 3 – 4 | !FALSE 4 – 1 |
29. При поступлении в неизолированную термодинамическую систему тепла в ходе необратимого процесса приращение её энтропии …
Видео:Центростремительное ускорение. 9 класс.Скачать

Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Видео:Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Видео:1989-0617 По часово́й стре́лке и про́тив часово́й стре́лки. Отрывок из лекции, русские субтитры.Скачать

Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
📹 Видео
движение по окружности задача 1Скачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Вопрос: в какую сторону вращается балерина? По часовой стрелке или против часовой?Скачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Твердое тело vs Материальная точка | Физика ЕГЭСкачать

Вращение против и по часовой стрелкеСкачать

Против часовой стрелки, а то у меня волосы на груди сваляются)) #shortsСкачать

Физика | Равномерное движение по окружностиСкачать

Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать