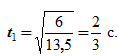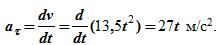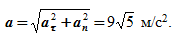В точке а траектории угол между векторами скорости

Глава 7. Кинематика точки.

7.8. Ускорение точки при естественном способе задания движения.

7.8.1. Даны нормальное а_n = 2,5 м/с 2 и касательное а_τ = 1,5 м/с 2 уско­рения точки. Определить полное ускорение точки. (Ответ 2,92)

7.8.2. Определить модуль ускорения точки, если его вектор а = 2,5n + 3,5τ, где n и τ — орты естественного триэдра. (Ответ 4,30)

7.8.3. Точка движется по криволинейной траектории с касательным ус­корением а_τ = 1,4 м/с 2 . Определить нормальное ускорение точки в момент времени, когда ее полное ускорение а = 2,6 м/с 2 . (Ответ 2,19)

7.8.4. Определить нормальное ускорение точки в момент времени, ког­да ускорение точки а = 1,5 м/с 2 , а угол между векторами ускорения и скорости равен 65°. (Ответ 1,36)

7.8.5. Точка движется по окружности. Определить радиус окружности, если в момент времени, когда скорость v = 10 м/с, вектор ускорения и вектор скорости, равный по модулю 1,2 м/с, образуют угол 30°. (Ответ 167)

7.8.6. Дан график касательного ускорения а_τ = а_τ (t) движения точки по окружности ради­уса 9 м. Определить полное ускорение в мо­мент времени t = 2 с, если при t_o = 0 скорость точки v₀ = 0.
(Ответ 3,74)

7.8.7. Ускорение точки а = 1 м/с. Векторы ускорения и скорости обра­зуют угол 45°. Определить скорость в км/ч, если радиус кривизны траектории ρ = 300 м. (Ответ 52,4)

7.8.8. Точка движется по окружности, радиус которой r = 200 м, с касательным ускорением 2 м/с 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени, когда ее скорость v = 10 м/с. (Ответ 14,0)

7.8.9. Точка движется по окружности, радиус которой r = 50 м, со скоростью v = 2t. Определить модуль полного ускорения в момент времени t = 5 с. (Ответ 2,83)

7.8.10. Задано уравнение движения точки по криволинейной траекто­рии: s = 0,2t 2 + 0,3t. Определить полное ускорение точки в момент времени t = 3 с, если в этот момент радиус кривизны траектории ρ = 1,5 м. (Ответ 1,55)

7.8.11. Определить скорость точки в момент времени, когда радиус кри­визны траектории ρ = 5 м, касательное ускорение а_τ = 2 м/с 2 , а tgβ = 3, где β — угол между векторами скорости и ускорения точки (Ответ 5,48)

7.8.12. Даны графики ускорения а_τ = а_τ(t) и а_n = a_n(t). Определить, какой угол в градусах образует полное ускорение с направлением скорости в момент времени t = 3 с. (Ответ 56,3)

7.8.13. По окружности радиуса r = 6 м движется точка со скоростью v = 3t. Определить угол в градусах между ускорением и скоростью точки в момент времени t = 1 с. (Ответ 26,6)

7.8.14. Точка движется по окружности радиуса r = 9 м. Определить скорость точки в момент времени, когда касательное ускорение а_τ = 2 м/с 2 , а вектор полного ускорения а образует угол 70 o c касательной к траектории. (Ответ 7,03)

7.8.15. Дан график скорости v = v(t) движения точки по окружности радиуса 8 м. Определить полное ускорение в момент времени t = 4 с. (Ответ 2,24)

7.8.16. Точка движется но окружности радиуса r = 200 м из состояния покоя с постоянным касательным ускорением а_τ = 1 м/с 2 . Опреде­лить полное ускорение точки в момент времени t = 20 с. (Ответ 2,24)

7.8.17. Точка движется по окружности радиуса r = 2 м. Нормальное ускорение точки меняется согласно закону а_n = 2t 2 . Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t = 1 с. (Ответ 45)

7.8.18. Задан закон движении точки по траектории: s = 0,5t 2 . Опреде­лить угол в градусах между векторами скорости и полного ускорения точки в момент времени t₁ = 3 с, когда радиус кривизны ρ = 4 м. (Ответ 66,0)

7.8.19. По окружности радиуса r = 1м движется точка согласно урав­нению s = 0,1t 3 . Определить полное ускорение точки в момент вре­мени t = 2 с. (Ответ 1,87)

7.8.20. Точка движется по криволинейной траектории с касательным ускорением а_τ = 2 м/с 2 . Определить угол в градусах между векто­рами скорости и полного ускорении точки в момент времени t = 2 с, когда радиус кривизны траектории ρ = 4м, если при t₀ = 0 скорость точки v₀ = 0. (Ответ 63,4)

Сборник коротких задач по теоретической механике.
Кепе О.Э.

Книга состоит из 1757 заданий которые предназначены для бысторого
контроля знаний на занятиях и зачетах а также для допуска к экзамену.
Задачи имеют ответы.

Издательство «Высшая школа» 1989 Москва

Также решение задач Кепе можно скачать здесь:
Мобильное приложение для Андроид:

Видео:Как находить угол между векторамиСкачать

Задачи для отработки кинематических понятий

Хорошо ли вы понимаете, какой смысл вкладывается в то или иное понятие или соотношение? Ниже мы предлагаем ряд качественных задач, с помощью которых вы можете проверить и углубить свои знания. Часть из них имеют подробные решения, другие предназначены для самостоятельного решения. Попытайтесь сначала все задачи решить самостоятельно. В случае неудачи при решении восьми первых задач не спешите прочесть всё решение. Иногда достаточно прочесть несколько строчек объяснения, т.е. получить небольшую подсказку, чтобы затем самостоятельно довести решение до конца.

Определить угол и перемещение материальной точки, движущейся по заданной траектории из точки А в точку В.

Вектор перемещения направлен из начальной точки в конечную и, следовательно, |Дг | = 2R. Путь определяется отрезком траектории между точками А и В:

Определить направление движения материальной точки через время t_x = 0,5 с и t₂ = 3 с после начала движения, если её движение вдоль оси ОХ описывается уравнением x = t-2t 2 .

Направление движения в конкретный момент времени определяется направлением вектора мгновенной скорости v и направлением бесконечно малого перемещения dr. Если проекция вектора скорости на выбранное направление положительная, то точка движется в этом направлении, если отрицательная — в противоположном.

Используем координатный способ описания движения:

Подставляем в полученную формулу значения и t₂ и находим v_x (/,) = 8 м/с; v_x (t₂) = -2 м/с . Следовательно, в момент времени *, точка движется в положительном направлении оси ОХ, а в момент времени t₂ — в противоположном.

Зависимость пройденного пути от времени для двух движущихся прямолинейно точек представлена кривыми 1 и 2. Какая кривая соответствует движению с возрастающей, а какая с убывающей скоростью?

Ускорение при прямолинейном движении а = . Для

кривой, направленной выпуклостью вниз, вторая производная положительная, а для кривой, направленной выпуклостью вверх, — отрицательная (см. приложение).

Поэтому кривая 1 соответствует замедленному движению, а кривая 2 — ускоренному.

На рисунке изображены графики двух прямолинейных движений I и II. Сравнить в I и II: а) ускорения; б) пути, пройденные за время г .

В этой задаче необходимо уточнить геометрическую интерпретацию пути и ускорения на графике скорости. Вспомним связь между скоростью и искомыми величинами.

1. Для прямолинейного движения ускорение

Учитывая геометрический смысл производной как тангенса угла наклона касательной, получим а_< = а_п .

2. По определению скорости в естественном способе

описания движения v = — . Движения I и II — равноускорен- dt

ные и отличаются только начальными скоростями:

МО = v o/ +at > v //(0 = v on + at —

Отсюда следует, что ds = vdt. Интегрируя от t = 0 до t = х , получаем

Геометрический смысл определённого интеграла — площадь между кривой v(f) и осью абсцисс от 0 до г . Следовательно:

Материальная точка, двигаясь по окружности радиусом R, совершила один оборот за 2 с. Чему равна средняя скорость пути и средняя скорость перемещения этой точки?

За один оборот точка прошла путь As = 2nR со средней

скоростью пути (|v|) = — = nR. Вектор перемещения при этом равен нулю, так как тело вернулось в исходную точку, следовательно, средняя скорость перемещения равна нулю:

В некоторый момент времени угол между векторами скорости v и ускорения а равен а > 90°. Каков характер движения в этот момент времени?

Используем естественный способ описания движения. Ускорение а можно представить в виде суммы двух составляющих (см. табл. 1):

Вектор нормального ускорения а_п всегда направлен к центру кривизны траектории, т.е. перпендикулярно v, и характеризует изменение скорости по направлению, а вектор тангенциального ускорения а_т направлен по касательной к траектории и характеризует изменение скорости по величине. Поэтому при наличии а_п Ф 0 движение происхо-

Видео:Угол между векторами. 9 класс.Скачать

iSopromat.ru

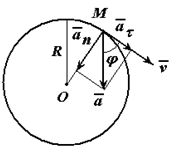
Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.

Видео:Угол между векторами | МатематикаСкачать

Задача

Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).

Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t₁, когда скорость будет равна 6 м/с (рисунок 1.6).

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Решение

Дифференцируя s по времени, находим модуль вектора скорости точки

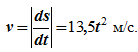
Подставляя в это выражение значение скорости, получим 6=13,5t₁ 2 , откуда находим

Касательное ускорение для любого момента времени равно

Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно

Модуль вектора полного ускорения точки равен

Угол между вектором полного ускорения и вектором скорости определим следующим образом:

📺 Видео

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

100 тренировочных задач #135 Угол между векторамиСкачать

105. Угол между векторамиСкачать

Угол между векторами | Геометрия 7-9 класс #100 | ИнфоурокСкачать

№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать

9 класс, 17 урок, Угол между векторамиСкачать

11 класс, 5 урок, Угол между векторамиСкачать

Угол между векторами. Уроки 11. Геометрия 9 классСкачать

Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать

Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать

№1040. Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба.Скачать

Скалярное произведение векторов. 9 класс.Скачать

найти угол между единичными векторамиСкачать

Угол между векторами.Скачать