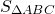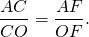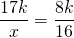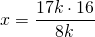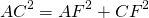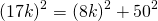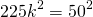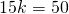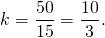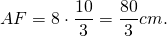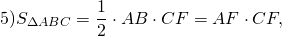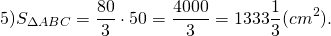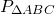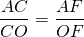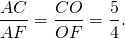В равнобедренный треугольник ab bc вписана окружность

Геометрия | 5 — 9 классы

В равнобедренный треугольник ABC (AB = BC) вписана окружность.

Через точку M, лежащую на стороне AB, проведена касательная к окружности, пересекающая прямую AC в точке N.

Найти боковую сторону треугольника ABC, если AC = CN = a, MB = 1 / 8AB.

Продолжим сторону $BC$ в два раза , тогда получим параллелограмм$ABNC’$ точка$CC’=b$ , заметим теперь что треугольники $MBO; C’ON$$O$ точка пересечения $NM$ с $BC$

Так как касательные проведенные с одной точки равны , то так как$AC$ основание данного треугольника , то точка касания окружности основанием симметрична , то есть$frac$

Если[img = 10] [img = 11] точка касания с окружностью , стороны [img = 12] [img = 13]

Если[img = 15] — точка пересечения [img = 16] с окружностью

[img = 18] , по той же причине

с другой стороны

Теперь заметим что окружность вписана в треугольники

Положим что угол[img = 22]

По формуле[img = 24]

это ответ[img = 26].

Равнобедренный треугольник ABC с основанием АС вписан в окружность с центром О?

Равнобедренный треугольник ABC с основанием АС вписан в окружность с центром О.

Площадь треугольника ABC 4 корня из 2, угол В равен 45 градусов.

Прямая, проходящая через точку О и середину BC, пересекает сторону AB в точке K.

Найдите площадь треугольника BCK.

Через произвольную точку D, основания AC равнобедренного треугольника ABC проведены прямые , параллельные боковым сторонам треугольника и пересекающими их в точках M и M?

Через произвольную точку D, основания AC равнобедренного треугольника ABC проведены прямые , параллельные боковым сторонам треугольника и пересекающими их в точках M и M.

Найти периметр BMDN, если AB = 10 см.

Треугольник abc равнобедренный основание àc = 18, в этот треугольник вписанна окружность и параллельно этой окружности проведена касательная котороя делит боковые стороны в точках d и e найти r?

Треугольник abc равнобедренный основание àc = 18, в этот треугольник вписанна окружность и параллельно этой окружности проведена касательная котороя делит боковые стороны в точках d и e найти r.

В равнобедренном треугольнике ABC (AB = BC) средняя линия, параллельная стороне BC, пересекается со вписанной окружностью в точке F, не лежащей на основании AC?

В равнобедренном треугольнике ABC (AB = BC) средняя линия, параллельная стороне BC, пересекается со вписанной окружностью в точке F, не лежащей на основании AC.

Докажите, что касательная к окружности в точке F пересекается с биссектрисой угла С на стороне АВ.

Начертите равнобедренный треугольник ABC?

Начертите равнобедренный треугольник ABC.

Через произвольную точку D, лежащую на стороне AB , проведите прямую , параллельную AC.

Докажите, что треугольник DBE равнобедренный.

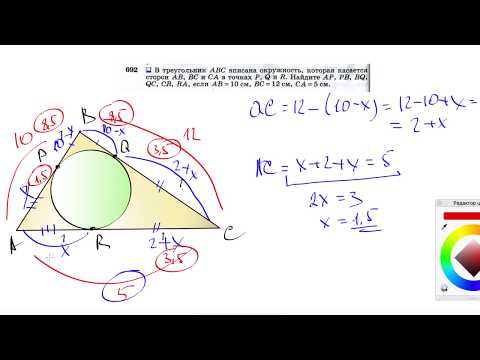
В треугольнике ABC вписана окружность, которая касается сторон AB и BC в точках E и F соответственно?

В треугольнике ABC вписана окружность, которая касается сторон AB и BC в точках E и F соответственно.

Касательная MK к этой окружности пересекает стороны AB и BC соответственно в точках M и K.

Найдите периметр треугольника BMK, если BE = 6см.

В треугольнике ABC проведена биссектриса BM?

В треугольнике ABC проведена биссектриса BM.

Точка K — точка касания вписанной окружности со стороной BC.

KM параллельна AB.

Найти сторону AB, если BC = 12, AC = 17.

В равнобедренный треугольник с боковой стороной 100, основанием 60 вписана окружность?

В равнобедренный треугольник с боковой стороной 100, основанием 60 вписана окружность.

Найти расстояние между точками касания окружностью боковых сторон.

В равнобедренный треугольник ABC (AB = AC) вписана окружность , касательная L к окружности параллельна прямой BC пересекает стороны AB и AC в точках K и O?

В равнобедренный треугольник ABC (AB = AC) вписана окружность , касательная L к окружности параллельна прямой BC пересекает стороны AB и AC в точках K и O.

Известно что периметр четырехугольника BTOC = 45 cм и TO : BC как 1 : 4 , вычислите радиус окружности.

Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно ?

Окружность вписанная в равнобедренный треугольник ABC касается его боковых сторон AB и BC в точках M и N соответственно .

Докажите что MN перпендикулярна AC.

На этой странице находится вопрос В равнобедренный треугольник ABC (AB = BC) вписана окружность?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Тр – треугольник. У – угол рассмотрим тр KFH и тр PHE У них : 1) КН = НЕ (по условию) 2) KF = PE (по условию) 3) у FKH = y HEP (т. К. они смежные равным углам) Следовательно, тр KFH = тр PHE по двум сторонам и углу между ними.

360градусов = 100% 90градусов = х% х = 90 * 100 / 360 = 25.

Угол AHB = 180 — 110 = 70 градусов Угол ABH = 180 — (AHB + BAH) = 180 — (70 + 90) = 20 Угол B = 2 * ABH = 20 * 2 = 40 градусов (т. К. биссектриса делит угол пополам) Угол С = 180 — (A + B) = 180 — (90 + 40) = 50 градусов Ответ : 40 градусов, 50 град..

TgB = AC : BC = 3 : 5 = 0, 6 Ответ 0, 6.

Tg В = АС : ВС = 3 : 5 = 0, 6 Ответ : 0, 6.

Вот так вроде. Извиняюсь, за не аккуратное решение.

Пусть в параллелограмме ABCD вершины A, B а также точка пересечения диагоналей O лежат в плоскости a (альфа). Рассмотрим диагональ AC. Две её точки — A и O — лежат в а, тогда вся диагональ лежит в а, так как если две точки прямой принадлежат плоско..

X = — 1, x = 3 — пределы .

Дано : аII АС ∠1 : ∠2 : ∠3 = 3 : 10 : 5 Найти : углы тр — каАВС Решение. Полученный углы составляют развернутый угол, градусная мера которого 180° Из отношения 3 : 10 : 5 сумма углов равна 3 + 10 + 5 = 18 частей 180 : 18 = 10° — — — — — приходится н..

Узнать ещё

Знание — сила. Познавательная информация

Окружность, вписанная в равнобедренный треугольник

Если в задача дана окружность, вписанная в равнобедренный треугольник, в ее решении могут быть использованы свойства касательных и свойство биссектрисы треугольника.

Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию .

Рассмотрим две задачи на вписанную в равнобедренный треугольник окружность.

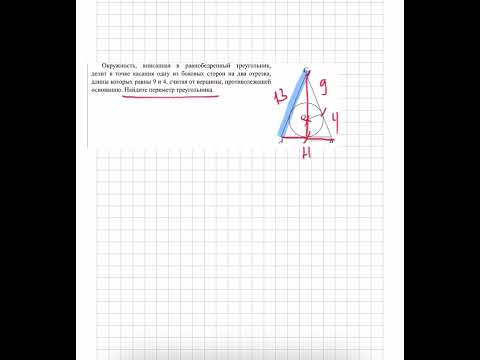
Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 8:9, считая от вершины угла при основании треугольника. Найти площадь треугольника, если радиус вписанной окружности равен 16 см.

окружность (O, r) — вписанная,

F, K, M, — точки касания со сторонами AB, BC, AC,

1) Пусть k — коэффициент пропорциональности (k>0). Тогда AM=8k см, MC=9k см.

2) По свойству касательных, проведенных из одной точки,

AF=AM=8k см, CK=MC=9k см.

Так как AC=BC, то BK=AM и BF=BK=8k см.

3) Центр вписанной окружности является точкой пересечения биссектрис треугольника.

Так как ∆ ABC — равнобедренный с основанием AB, то CF — высота, медиана и биссектриса ∆ ABC.

4) Рассмотрим треугольник AFC.

∠AFC=90, AF=8k см, AC=AM+MC=17k см.

OF=r. Пусть CO=x см, тогда

CO=34 см, CF=CO+OF=34+16=50 см.

По теореме Пифагора:

Ответ: 1333 1/3 кв.см.

Центр окружности, вписанной в равнобедренный треугольник, делит высоту, проведенную к основанию, в отношении 5:4. Найти периметр треугольника, если боковая сторона меньше основания на 15 см.

Дано: ∆ ABC, AC=BC,

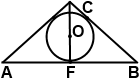
окружность (O, r) — вписанная,

CF — высота, CO:OF=5:4, AC

1) Рассмотрим ∆ ACF — прямоугольный (так как CF — высота треугольника по условию).

Центр вписанной в треугольник окружности есть точка пересечения его биссектрис.

По свойству биссектрисы треугольника,

Пусть k — коэффициент пропорциональности, тогда AC=5k см, AF=4k см, AB=2AF=8k см.

Следовательно, AC=BC=5∙5=25 см, AB=8∙5=40 см.