Задачи на свойства равнобедренного треугольника (7 видео)

Задачи на свойства равнобедренного треугольника

Равнобедренный треугольник — треугольнику которого две стороны равны.
Равные стороны называют боковыми сторонами, а третью сторону — основанием.

Свойства равнобедренного треугольника были известны с давних времен. Еще древние вавилоняне (II в. до н.э.) знали, что углы у основания равнобедренного треугольника равны. Любой треугольник можно разрезать на равнобедренные треугольники.

Содержание

Свойства и признаки равнобедренного треугольника
ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ:
Теоретический тест с последующей самопроверкой
Свойства равнобедренного треугольника: теория и задача
Определение равнобедренного треугольника
Свойства равнобедренного треугольника
Свойство 1
Свойство 2
Свойство 3
Пример задачи
Решение задач по теме «Треугольники» (7-й класс)
🎥 Видео

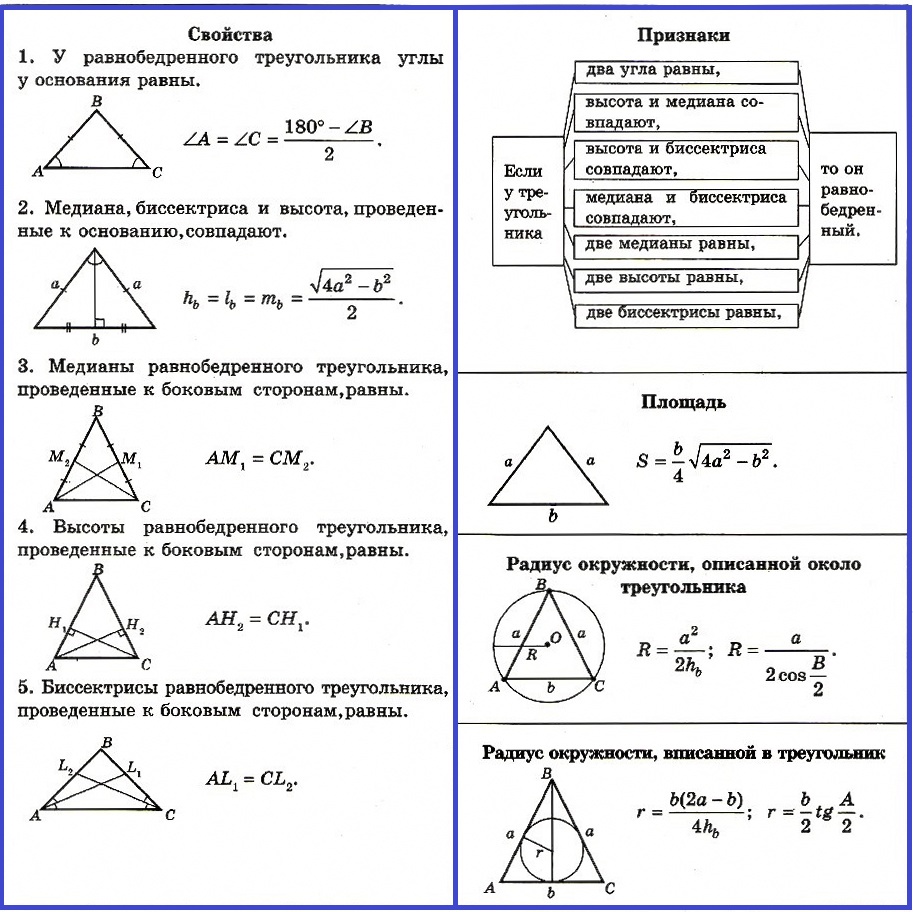
Свойства и признаки равнобедренного треугольника

Свойства равнобедренного треугольника:
1. У равнобедренного треугольника углы у основания равны (теорема).
2. Медиана, биссектриса и высота, проведенные к основанию, совпадают (теорема).
3. Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны.
4. Высоты равнобедренного треугольника, проведенные к боковым сторонам, равны.
5. Биссектрисы равнобедренного треугольника, проведенные к боковым сторонам, равны.

Признаки равнобедренного треугольника:
Если у треугольника есть один из нижеуказанных признаков, то он равнобедренный:
— два угла равны,
— высота и медиана совпадают,
— высота и биссектриса совпадают,
— медиана и биссектриса совпадают,
— две медианы равны,
— две высоты равны,
— две биссектрисы равны.

ПРИМЕРЫ РЕШЕНИЯ
КЛЮЧЕВЫХ ЗАДАЧ:

Задача № 1. Дано: ΔABC — равносторонний, ΔADC — равнобедренный (AD=CD), AC — общая сторона, BC = 8 см, P_ADC > P_ABC в 1,5 раза. Найти: CD.

Задача № 2. Дано: ΔABC — равнобедренный, AB = BC, AD — медиана, AB + BD = 27 см, AC + CD = 21 см. Найти: AB, BC, AC.

Задача № 3. Дано: ΔABC — равнобедренный, AB = BC, ∠1 = 130°. Найти: ∠2.

Теоретический тест
с последующей самопроверкой

Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является биссектрисой и медианой.
В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) два его угла равны.
В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Если в треугольнике два угла равны, то этот треугольник является:
а) равносторонним;
б) равнобедренным;
в) прямоугольным.
Если в треугольнике две стороны равны, то:
а) у него равны два угла;
б) у него все углы равны;
в) этот треугольник равносторонний.

Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение: б) может быть верно.
Если треугольник равносторонний, то: а) он равнобедренный; б) все его углы равны; в) любая его высота является биссектрисой и медианой.
В каком треугольнике только одна его высота делит треугольник на два равных треугольника? б) в равнобедренном.
Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение: а) всегда верно.
Если треугольник равнобедренный, то: в) два его угла равны.
В каком треугольнике любая его высота делит треугольник на два равных треугольника? в) в равностороннем.
Если в треугольнике два угла равны, то этот треугольник является: б) равнобедренным.
Если в треугольнике две стороны равны, то: а) у него равны два угла.

Вы смотрели конспект по теме «Равнобедренный треугольник + ЗАДАЧИ по теме». Выберите дальнейшие действия:

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Свойства равнобедренного треугольника: теория и задача

В данной публикации мы рассмотрим определение и свойства равнобедренного треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Определение равнобедренного треугольника

Равнобедренным называют треугольник, в котором две стороны имеют одинаковую длину (называются боковыми). Оставшаяся третья сторона является основанием фигуры.

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Свойства равнобедренного треугольника

Свойство 1

В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны. Это значит, что α = β.

Если углы при основании треугольника равны, значит он является равнобедренным.

Свойство 2

В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой угла и медианой, проведенной к основанию.

BD – медиана и высота к основанию AC, а также биссектриса угла ABC.

Свойство 3

Центры вписанной и описанной вокруг равнобедренного треугольника окружностей лежат на одном отрезке, являющимся биссектрисой, медианой и высотой, проведенной к основанию.

O₁ и O₂ – расположены на одном отрезке;
R – радиус описанной окружности;
r – радиус вписанной окружности.

Видео:Свойства равнобедренного треугольника. Практическая часть. 7 класс.Скачать

Пример задачи

Дан равнобедренный треугольник, в котором длина основания в полтора раза больше боковой стороны. Периметр фигуры равняется 14 см. Найдите длины всех сторон.

Решение
Нарисуем чертеж согласно условиям задачи, приняв боковую сторону за a.

В таком случае, основание AC равняется 1,5a.
Периметр треугольника – это сумма всех его сторон:
AB + BC + AC = a + a + 1,5a = 3,5a = 14.
Т.е. a = 4.

Следовательно, боковая сторона равна 4 см, а основание – 6 см (4 см ⋅1,5).

Видео:Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Решение задач по теме «Треугольники» (7-й класс)

Разделы: Математика

Класс: 7

Цели и задачи урока:

обобщить, закрепить и углубить знания по изученной теме;
формировать умение обучаемых доказывать равенство данных треугольников, опираясь на изученные признаки, применять свойства равнобедренного треугольника;
отработать навыки решения простейших задач на построение с помощью циркуля и линейки;

развивать логическое мышление, самостоятельность учащихся при решении заданий; умение на практике применять знания, полученные на уроках;

воспитывать познавательную активность, упорство в достижении поставленной цели, культуру умственного труда

Оборудование:

интерактивная доска или наглядный материал (готовые чертежи);
карточки с задачами для индивидуальной работы на доске;
таблицы с признаками равенства треугольников.

Тип урока: урок закрепления полученных знаний.

Ход урока

І. Организационный момент.

Учитель:

— Тема урока: «Решение задач по теме «Треугольники»». Мы сегодня обобщим и систематизируем знания по данной теме и наша цель: подготовиться к контрольной работе, которая будет на следующем уроке.

— Откройте дневники и запишите домашнее задание.

I уровень: № 120(б), 121;
II – III уровень: №160 (б), 162(б).

II. Актуализация опорных знаний.

1. У доски двое учащихся решают задачи по карточкам.

Начертите равнобедренный треугольник АВС с основанием АС. С помощью циркуля и линейки проведите медиану АА1 к боковой стороне ВС.

Дано: АО = BO, СО = DO, CO = 5см, ВО = 3см, BD = 4см.
1)Докажите, что САО = DBO.
2)Найдите периметр треугольника САО.

2. Для остальных учащихся класса организована фронтальная работа.

Цель: повторить основные вопросы теории темы «Равнобедренный треугольник и его свойства» с помощью теста. (Вопросы теста – на интерактивной доске)

Теоретический тест. [1]
В каждом задании из трёх предложенных ответов выберите верный и обоснуйте его. Верных ответов может быть несколько. Подумайте и ответьте на вопрос. (А я считаю, что…; я не согласна с этим утверждением, т.к. …)

1) Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Ответ: б), если медиана проведена к основанию равнобедренного треугольника.

2) Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является биссектрисой и медианой.
Ответ: а), б), и в), равносторонний треугольник является частным случаем равнобедренного треугольника; в равнобедренном треугольнике углы при основании равны, поэтому в равностороннем треугольнике все углы равны.

3) В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответ: б), высота, проведённая к основанию равнобедренного треугольника.

4) Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
Ответ: а)

5) Если треугольник равнобедренный, то
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
Ответ: в), т.к. равнобедренный треугольник не всегда является равносторонним; медиана, проведённая к боковой стороне равнобедренного треугольника, не является биссектрисой и высотой, если треугольник не равносторонний.

6) В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Ответ: в).

Учитель:
— Мы с вами повторили материал темы «Равнобедренный треугольник и его свойства», а теперь повторим признаки равенства треугольников. (Обратить внимание обучающихся на таблицы с признаками равенства треугольников)

3. Задачи в рисунках (на интерактивной доске).

Учитель:
— Определите, являются ли равными треугольники на рисунках.

— Сколько пар равных элементов должно быть в равных треугольниках?