В основании четырехугольной пирамиды sabcd лежит четырехугольник abcd

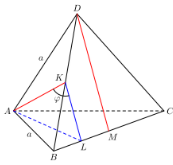
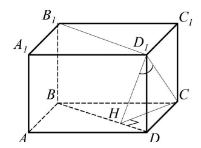
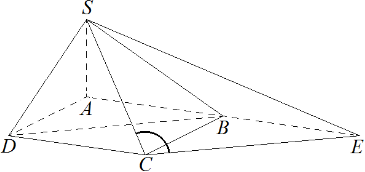
Задание 14. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 8 и ВС = 6. Длины боковых рёбер пирамиды SA= √21, SB = √85, SD = √57.

а) Докажите, что SA — высота пирамиды.

б) Найдите угол между прямыми SC и BD.

а)Рассмотрим треугольник SAB, в котором по условию задания: SA= √21, AB = 8, SB = √57.Можно заметить, что

и согласно обратной теореме Пифагора треугольникSAB – прямоугольный, с гипотенузой SB и катетами SA и AB.

Рассмотрим треугольник SAD со сторонами: SD = √57, SA= √21, AD = 6 (так как в основании пирамиды лежит четырехугольник, поэтому AD = BC). Здесь также:

и по обратной теореме Пифагора имеем прямоугольный треугольник SAD с гипотенузой SD и катетами SA и AD.

Так как , то по признаку перпендикулярности прямой и плоскости и SA–высота пирамиды.

б)Так как ABCD – прямоугольник, то точка O лежит на пересечении его диагоналей и делит их пополам, то есть, O–середина отрезка BD. Сделаем построение – отрезок KO как средняя линия треугольника SAC, причем, . Тогда угол между SC и BDбудет также равен углу KOD.

Найдем косинус угла SOD из треугольника KOD. В соответствии с теоремой косинусов, имеем:

Рассмотрим прямоугольный треугольник SDC (прямоугольный, так как и — по теореме о трех перпендикулярах получаем, что ). По теореме Пифагора:

Тогда KO = SC:2 = 11:2. Далее, диагональ

Следовательно, DO = DB:2 = 5. Точка K – середина SA, имеем: и

Получаем косинус угла:

Ответ:

Видео:Задание 14 | 2 вариант Ященко ЕГЭ профиль 2021 | В основании четырехугольной пирамиды прямоугольникСкачать

В основании четырехугольной пирамиды sabcd лежит четырехугольник abcd

БАЗА ЗАДАНИЙ

Задание № 13. Стереометрия с доказательством.

1. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 5. На его ребре BB ₁ отмечена точка K так, что KB=4. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что A ₁ P:PB ₁ =3:1, где P — точка пересечения плоскости α с ребром A ₁ B ₁ .
б) Найдите угол наклона плоскости α к плоскости грани BB ₁ C ₁ C.

2. В кубе ABCDA ₁ B ₁ C ₁ D ₁ все рёбра равны 5. На его ребре BB ₁ отмечена точка K так, что KB=4. Через точки K и C ₁ проведена плоскость α, параллельная прямой BD ₁ .
а) Докажите, что A ₁ P:PB ₁ =3:1, где P — точка пересечения плоскости α с ребром A ₁ B ₁ .
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.

4. В правильной треугольной пирамиде SABC сторона основания AB=6, а боковое ребро SA=4. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Ответ: б) 8 + 2√2

5. В правильной треугольной пирамиде SABC сторона основания AB=60, а боковое ребро SA=37. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите расстояние от вершины A до плоскости α.
Ответ: б) 5√3

7. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=6. Длины боковых рёбер пирамиды SA=3, SB=5, SD=3√5.
а) Докажите, что SA— высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
Ответ: б) 2,4

8. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых рёбер пирамиды SA=√21, SB=√85, SD=√57.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.

9. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB=5 и диагональю BD=9. Все боковые рёбра пирамиды равны 5. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF=BE=4.
а) Докажите, что плоскость CEF параллельна ребру SB.

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

10. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона основания AB равна 6, а боковое ребро AA ₁ равно 2√2. На рёбрах AB, A ₁ B ₁ и B ₁ C ₁ отмечены точки M, N и K соответственно, причём AM = B ₁ N= C ₁ K=2.
а) Пусть L — точка пересечения плоскости MNK с ребром AC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Ответ: б) 15

11. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона AB основания равна 6, а боковое ребро AA ₁ =3. На ребре AB отмечена точка K так, что AK=1. Точки M и L— середины рёбер A ₁ C ₁ и B ₁ C ₁ соответственно. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) 3/4

12. В правильной четырёхугольной призме ABCDA ₁ B ₁ C ₁ D ₁ сторона AB основания равна 8, а боковое ребро AA ₁ равно 4√2. На рёбрах BC и C ₁ D ₁ отмечены точки K и L соответственно, причём BK= C ₁ L=2. Плоскость γ параллельна прямой BD и содержит точки K и L.
а) Докажите, что прямая A ₁ C перпендикулярна плоскости γ.
б) Найдите расстояние от точки B до плоскости γ.

13. В основании прямой треугольной призмы ABCA ₁ B ₁ C ₁ лежит равнобедренный (AB=BC) треугольник ABC. Точка K— середина ребра A ₁ B ₁ , а точка M делит ребро AC в отношении AM:MC=1:3.
а) Докажите, что KM⊥AC.
б) Найдите угол между прямой KM и плоскостью ABB ₁ , если AB=6, AC=8, AA ₁ = 3.

14. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известны длины рёбер: AB=2√2, AD=6, AA₁=10. На рёбрах AA₁ и BB₁ отмечены точки E и F соответств., причём A ₁ E:EA =3:2 и B ₁ F:FB=3:7. Точка T — середина ребра B ₁ C ₁ .
а) Докажите, что плоскость EFT проходит через точку D ₁ .
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Ответ: б) 22,5

а) Докажите, что плоскость EFT проходит через вершину D₁.

б) Найдите угол между плоскостью EFT и плоскостью AA₁B₁.

16. На ребрах CD и BB1 куба ABCDA₁B₁C₁D₁ c ребром 12 отмечены точки Р и Q соответственно, причем DP=4, а B ₁ Q=3. Плоскость APQ пересекает ребро CC ₁ в точке М.
а) Докажите, что точка М является серединой ребра CC ₁ .
б) Найдите расстояние от точки С до плоскости APQ.

17. В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM=DN=4 и АК=3.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки К до плоскости SBC.

18. В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а высота равна 1. На ребрах АВ, АС и AS отмечены точки М, N и К соответственно, причем АМ=AN=3 и AK=7/4.
а) Докажите, что плоскости MNK и SBC параллельны.
б) Найдите расстояние от точки M до плоскости SBC.

19. Основанием прямой четырехугольной призмы ABCDA ₁ B ₁ C ₁ D ₁ является квадрат ABCD со стороной 4, высота призмы равна 6. Точка K делит ребро AA ₁ в соотношении AK:KA ₁ =1:2. Через точки K и B проведена плоскость α, параллельная прямой AC и пересекающая ребро DD ₁ в точке M.
а) Докажите, что плоскость α делит ребро DD ₁ в отношении DM:MD ₁ =2:1.
б) Найдите площадь сечения.
Ответ: б) 8√6

20. В правильной треугольной призме ABCA ₁ B ₁ C ₁ сторона AB основания равна 12, а боковое ребро AA ₁ равно 3√6. На ребрах AB и B ₁ C ₁ отмечены точки K и L соответственно, причем AK=2, B ₁ L=4. Точка M середина A ₁ C ₁ . Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ.
б) Найдите расстояние от точки C до плоскости γ.
Ответ: б) √2

21. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=√5 и BC=2. Длины боковых рёбер пирамиды SA=√7, SB=2√3, SD=√11.
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
Ответ: б) 30

22. В правильной четырехугольной пирамиде SABCD все ребра равны 5. На ребрах SA, AB, BC взяты точки P, Q, R соответственно так, что PA=AQ=RC=2.
а) Докажите, что плоскость PQR перпендикулярна ребру SD.
б) Найдите расстояние от вершины D до плоскости PQR.
Ответ: б) 7/2

23. В треугольной пирамиде PABC с основанием ABC известно, что AB=13, PB=15, cos PBA=48/65. Основанием высоты этой пирамиды является точка C. Прямые PA и BC перпендикулярны.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите объем пирамиды PABC.
Ответ: б) 90

24. Основанием прямой треугольной призмы ABCA ₁ B ₁ C ₁ является прямоугольный треугольник ABC с прямым углом C. Прямые CA ₁ и AB ₁ перпендикулярны.
а) Докажите, что AA ₁ =AC.
б) Найдите расстояние между прямыми CA ₁ и AB ₁ , если AC = 6, BC = 3.
Ответ: б) √2

6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.

3. Сечением прямоугольного параллелепипеда ABCDA ₁ B ₁ C ₁ D ₁ плоскостью α, содержащей прямую BD ₁ и параллельной прямой AC, является ромб.
а) Докажите, что грань ABCD— квадрат.
б) Найдите угол между плоскостями α и BCC ₁ , если AA ₁ =10, AB=12.

База заданий сформирована из Официального Банка заданий ФИПИ,

Открытого банка заданий ЕГЭ, а также из реальных вариантов ЕГЭ прошлых лет.

Видео:МА2010109. В основании пирамиды MABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = 33, все боСкачать

14. Стереометрия

Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.

Примеры ответов: 7 или здесьисейчас или 3514

Угол между скрещивающимися прямыми, между прямой и плоскостью

В правильном тетраэдре АВСD точка К – середина ВD, точка М – середина ВС. Найдите угол между прямыми АК и DМ.

1) Дополнительное построение: пусть точка L – середина ВМ. Тогда KL – средняя линия треугольника ВDМ; значит, KL||DM, и потому искомый угол есть $varphi=angle AKL$.

Величину $varphi$ мы вычислим по теореме косинусов из треугольника $AKL$. Предварительно найдём стороны этого треугольника.

Из треугольника АВD находим АК как высоту в равностороннем треугольнике:

$AK=displaystylefrac<asqrt>$, где a – ребро тетраэдра.

Остаётся найти сторону АL. Это можно сделать из треугольника АВL, в котором АВ=а, ВL= $displaystylefrac$, $angle ABL=60^$. По теореме косинусов получим:

Теперь возвращаемся к треугольнику АКL. По теореме косинусов:

$AL^2=AK^2+KL^2-2cdot AKcdot ALcdot cosvarphi$

Подставляем найденные длины сторон:

Тогда искомый угол – это $arccosdisplaystylefrac$.

Площадь боковой поверхности прямоугольного параллелепипеда АВСDА₁В₁С₁D₁ равна $6sqrt$, AB = $sqrt$, AA₁ = $sqrt$. Вычислите угол между плоскостью В₁ВD и прямой СD₁.

$Проведём CH!perp!BD. Поскольку DD_1!perp!ABC и CH!subset!ABC,,то DD_1!perp!CH.\Таким образом,,CH перпендикулярен двум пересекающимся прямым,,BD,,и DD_1,,лежащим в\плоскости B_1BD,,а,,значит,,является перпендикуляром к этой плоскости. Тогда CD_1 -\наклонная,,а D_1H — её проекция на эту плоскость,,и углом между прямой CD_1 и плоскостью\B_1BD является угол CD_1H.$

По теореме Пифагора из треугольника BCD получим $BD^2=BC^2+CD^2$, откуда BD = 5.

По теореме Пифагора из треугольника $CDD_1$ получим $CD_1^2=CD^2+DD_1^2$, откуда $CD_1=2sqrt$.

Из прямоугольного треугольника $CHD_1$ получим:

Значит, $angle CD_1H=45^$.

В правильной треугольной призме ABCA₁B₁C₁ боковое ребро равно стороне основания. Найдите угол между прямой АА₁ и плоскостью АВС₁.

Угол между прямой и плоскостью не изменится при параллельном сдвиге прямой. Поскольку СС1 параллельна АА1, искомый угол $varphi$ есть угол между прямой СС1 и плоскостью АВС1.

Пусть М — середина АВ, пусть АВ=а. Проведём высоту СН в треугольнике СС1М. Покажем, что СН — перпендикуляр к плоскости АВС1. Для этого нужно предъявить две пересекающиеся прямые этой плоскости, перпендикулярные СН.

Первая прямая очевидна — это С1М. В самом деле, $CH!perp! C_1M$ по построению.

Вторая прямая — это АВ. Действительно, проекцией наклонной СН на плоскость AВC служит прямая СМ; при этом $AB!perp! CM$. Из теоремы о трёх перпендикулярах следует тогда, что $AB!perp! CH$.

Итак, $CH!perp! ABC_1$.

Стало быть, угол между СС1 и АВС1 есть $varphi=angle CC_1H=angle CC_1M$.

В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 8 и BC = 6. Длины боковых рёбер пирамиды $SA=sqrt,,SB=sqrt,,SD=sqrt$.

а) Докажите, что $SA$ — высота пирамиды.

б) Найдите угол между прямыми $SC$ и $BD$.

а) В треугольнике $SAB$ имеем:

поэтому треугольник $SAB$ прямоугольный с гипотенузой $SB$ и прямым углом $SAB$. Аналогично, из равенства

получаем, что $angle SAD=90^$. Так как прямая $SA$ перпендикулярна прямым $AB$ и $AD$ прямая $SA$ перпендикулярна плоскости $ABD$ по признаку перпендикулярности прямой и плоскости.

б) Дополнительное построение: на прямой отметим такую точку E, что BDCE — параллелограмм, тогда $BE=DC=AB;,и;DB = CE$. Найдём угол SCE. По теореме Пифагора:

$quad AC=BD=sqrt=10; SC=sqrt=11;и;SE^2=SA^2+AE^2=277. \ По теореме косинусовcolon \[3pt] beginqquad SE^2=SC^2+CE^2-2SCcdot CE&cdotcosangle SCE; 277=121+100-220cosangle SCE; \ &cosangle SCE = -displaystylefrac.end$
Искомый угол равен $arccosdisplaystylefrac$.

В правильной шестиугольной пирамиде SABCDEF с вершиной S боковые рёбра равны 2, а сторона основания – 1.

а) Докажите, что плоскость, проходящая через вершину S и середины рёбер AF и СD перпендикулярна основанию.

б) Найдите косинус угла между прямой АС и плоскостью SAF.

а) Проведем эту плоскость. Так как, плоскость проходит через середины ребер К и N , на отрезке KN будет лежать центр правильного шестиугольника О. Значит, отрезок SO будет являться высотой правильной шестиугольной пирамиды. Значит, по признаку перпендикулярности плоскостей плоскость SKN будет перпендикулярна плоскости основания.

б) Так как пирамида правильная, то KN будет параллельно АС. Значит, искомый угол – угол между KN и SAF. Точнее возьмем отрезок ОК.

ОК перпендикулярно FA, так как в основании правильный шестиугольник.

SK перпендикулярно AF, так как треугольник AFS равнобедренный (по свойству равнобедренного треугольника о том, что медиана является высотой).

Значит, AF перпендикулярно плоскости KSO, а значит, перпендикулярно любой прямой, лежащей в этой плоскости.

Проведем отрезок ОН перпендикулярно SK.

ОН перпендикулярно SK. AF перпендикулярно ОН, значит, по признаку перпендикулярности прямой и плоскости ОН перпендикулярно плоскости ASF, то есть, точка Н является проекцией точки О на плоскость SAF.

Точка К проецируется в саму себя. Значит, угол между плоскостью ASF и прямой ОК – угол ОКН.

Найдем SK. Треугольник SAF – равнобедренный, значит, $SA=2, AK=0,!5$. Тогда SK по теореме Пифагора будет равно: $SK=displaystylesqrt<4-<smallfrac>>=frac<sqrt>$.

ОК – высота в равностороннем треугольнике AFO, значит, $OK=displaystylefrac<sqrt>$.

Тогда найдем косинус угла OKS по определению тригонометрической функции:

В основании четырехугольной пирамиды MABCD лежит прямоугольник ABCD со сторонами $AB=displaystylesqrt $ и $BC=displaystyle 2sqrt $. Длины боковых рёбер пирамиды $MA=5, MB=6, MD=sqrt$.

а) Докажите, что MA – высоты пирамиды.

б) Найдите угол между прямой MC и плоскостью AMB.

а) По определению, высота – это перпендикуляр, опущенный из вершины пирамиды на противоположную плоскость.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Рассмотрим треугольник MAB:

Тогда по теореме, обратной теореме Пифагора, угол MAB – прямой.

Рассмотрим треугольник MAD:

Тогда по теореме, обратной теореме Пифагора, угол MAD – прямой.

Прямая MA перпендикулярна двум пересекающимся прямым AB и AD, лежащим в плоскости основания, значит, перпендикулярна и всей этой плоскости.

Тогда MA – высота пирамиды, что и требовалось доказать.

б) Из того факта, что MA- высота, следует, что эта прямая перпендикулярна плоскости основания и любой прямой, лежащей в этой плоскости, в том числе прямой BC.

Также BC перпендикулярна AB, так как в основании пирамиды лежит прямоугольник.

Тогда прямая BC перпендикулярна двум пересекающимся прямым AB и MA, лежащим в плоскости AMB, значит, перпендикулярна и всей этой плоскости.

Тогда MC – наклонная, BC – перпендикуляр, а MB – проекция.

Угол между прямой MC и плоскостью AMB – это угол между прямой MC и её проекцией MB на эту плоскость, откуда угол CMB – искомый.

Рассмотрим треугольник CMB.

Угол CBM – прямой, так как CB перпендикулярно плоскости AMB.

🔍 Видео

№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать

Геометрия В правильной четырёхугольной пирамиде SABCD с основанием ABCD проведено сечение черезСкачать

10 кл .Егэ. В правильной четырехугольной пирамиде SABCD точка О центр основания. S--вершина,SO=15Скачать

10 кл.Егэ. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S верСкачать

Вариант #20 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать

Стереометрия, номер 28.1Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Найти площадь поверхности правильной четырехугольной пирамидыСкачать

Геометрия Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SBСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В основании четырехугольной пирамиды SABCD лежит квадрат со стороной 1Скачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

В правильной четырехугольной пирамиде точка О центр основаниСкачать

#121. Задание 8: четырехугольная пирамидаСкачать

Найдите отрезок АС в правильной четырехугольной пирамидеСкачать

ЕГЭ Задание 14 Угол между прямыми Координатно векторный методСкачать