В окружности радиуса r хорды ab и cd

Геометрия | 10 — 11 классы

В окружности радиуса R проведены две взаимно перпендикулярные хорды AB и CD, пересекающиеся в точке M .

Как доказать, что AC ^ 2 + BD ^ 2 = 4R ^ 2.

Если провести диаметр OY (это я его так обозначил, чтобы как — то потом называть), параллельно CD и перпендикулярно (само собой) AB, то он пройдет через середину AB, то есть точки A и B симметричны относительно OY ;

Теперь надо построить хорду C1D1, симметричную CD относительно OY ; ясно, что она параллельна CD и перпендикулярна AB, ясно, что C1D1 = CD ; и вообще — CDD1C1 это прямоугольник.

Что означает, что CD1 — диаметр.

Поскольку при зеркальном отражении относительно OY точка A переходит в B, а точка D — в точку D1, то BD = AD1 ; (по определению равенства фигур, между прочим).

Остается заметить, что, раз CD1 — диаметр, то треугольник ACD1 — прямоугольный, и записать для него теорему Пифагора.

В окружности проведены Две взаимно перпендикулярные хорды?

В окружности проведены Две взаимно перпендикулярные хорды.

них делится другой хордой на отрезки, равные 3 и 7.

Найдите расстояние от

центра окружности до каждой из хорд.

Задана окружность с центром О и с хордой CD?

Задана окружность с центром О и с хордой CD.

Радиус OE проведен перпендикулярно хорде CD.

Докажите, что хорды CE и DE равны.

Из одной точки окружности проведены две взаимно перпендикулярные хорды которые удалены от центра на 6 см и 10 см?

Из одной точки окружности проведены две взаимно перпендикулярные хорды которые удалены от центра на 6 см и 10 см.

Найдите длину хорды.

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Каждая из них делится другой хордой на отрезки, равные 4 и 6.

Найдите расстояние от центра окружности до каждой хорды.

Две окружности с равными радиусами пересекаются в двух точках?

Две окружности с равными радиусами пересекаются в двух точках.

Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.

В окружности с центром в точке О и радиусом ОС = 25 проведена хорда CD = 40?

В окружности с центром в точке О и радиусом ОС = 25 проведена хорда CD = 40.

Найдите расстояние от центра О до хорды CD.

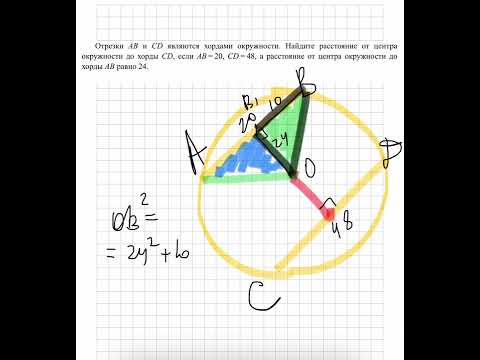
Из внешней точки проведены к окружности две взаимноперпендикулярные касательные, радиус окружности 10 см?

Из внешней точки проведены к окружности две взаимно

перпендикулярные касательные, радиус окружности 10 см.

Найдите расстояние от

данной точки до точки касания.

В окружности с центром в точке О и радиусом ОС = 25 проведена хорда CD = 40?

В окружности с центром в точке О и радиусом ОС = 25 проведена хорда CD = 40.

Найдите расстояние от центра О до хорды CD.

Две равные окружности пересекаются в точках А и В?

Две равные окружности пересекаются в точках А и В.

Через точку А проведена хорда АМ одной окружности, а через точку В — хорда ВN другой окружности, причем АМ и BN параллельны.

Доказать, что эти хорды равны.

Две равные окружности пересекаются в точках A и B ?

Две равные окружности пересекаются в точках A и B .

Через точки А проведена хорда АМ одной окружности , а череш точку B — хорда BN другой окружности , причем AM и Bb паралелны .

Доказать что эти хорды равны.

На этой странице находится вопрос В окружности радиуса R проведены две взаимно перпендикулярные хорды AB и CD, пересекающиеся в точке M ?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Если не сложно дайте лучший ответ, пожалуйста.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Свойства хорд

свойства хорды в окружности

Свойство 1
1. Диаметр окружности CD, перпендикулярный хорде AB, делит хорду пополам, и наоборот: CD ? AB AF = FB .

Свойство 2
2. Равные хорды хорды находятся на равном расстоянии от центра окружности: AB = CD ? OE = OF .

Свойство 3
3. Дуги окружности, заключенные между параллельными хордами, равны между собой: AB || CD ? ? AC = ? BD .

Свойство 4
4. Если хорды AB и CD окружности пересекаются в точке S, то AS • SB = CS • SD .

Свойство 5
5. Если хорда AB проходит через внутреннюю точку M круга радиуса R и расстояние до M от центра OM = d , то AM • MB = R 2 — d 2 .

📽️ Видео