Укажите следствия из аксиомы параллельных прямых (5 видео)

Геометрия. 7 класс

Следствия из аксиомы

Выберите все правильные варианты ответа.

Укажите следствия из аксиомы параллельных прямых.

Если прямая пересекает одну из параллельных прямых, то она не может пересекать другую.

Если три прямые параллельны, то любые две из них параллельны друг другу.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей прямой, то они параллельны.

Да или нет

Выберите правильный вариант ответа из выпадающего списка.

Через точку М проведена прямая b, параллельная прямой a.

Можно ли через точку М провести еще одну прямую, параллельную данной? .

Можно ли провести две прямых параллельных данной? .

Можно ли это доказать? .

Найдите углы

Впишите недостающие элементы доказательства в таблицу.

Прямая с пересекает прямые а и b так, что ∠2 = 30 о , ∠1 в 5 раз больше. Докажите, что а || b.

Какие прямые параллельны?

Введите с клавиатуры пропущенные элементы.

Укажите в тексте параллельные прямые.

Если ∠1 =∠4, то прямые и параллельны. Если ∠2 =∠3, то прямые и параллельны.

Взаимное расположение прямых

Выделите цветом верный ответ.

Даны четыре прямые a, b, m, n. Причём прямые a и b перпендикулярны прямой n, прямые a и m параллельны. Каково взаимное положение прямых b и m?

Сколько точек и прямых?

Укажите, сколько точек и прямых можно построить по условию задачи.

Аксиома

Укажите утверждение, которое не является аксиомой.

Через любые две точки проходит прямая, и притом только одна.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Восстановите последовательность

Восстановите правильную последовательность доказательства.

Дано: ΔABC – прямоугольный

Докажите: AC ║ BD.

∠A = ∠ABK = 47° накрест лежащие при пересечении прямых AC и KD и секущей AB.

∠KBD = 180° развёрнутый.

∠ABK = 180° – 90° – 43° = 47°

Пересекающиеся прямые

Вставьте пропущенные элементы текста.

Через вершины A и B ΔABC проведены прямые m и n параллельные сторонам. Докажите, что прямые m и n пересекаются:

по условию m BC;

Значит m прямую n

т.к. n AC, согласно следствию из аксиомы параллельных прямых.

Признаки параллельности

Подчеркните правильный вариант ответа.

Продолжите предложение: прямые параллельны, если равны…

Параллельные прямые

Введите с клавиатуры пропущенные элементы текста.

Прямые a, b, c пересечены секущей m так, что: b || c, ∠1 = 57°, ∠2 = 123°. Докажите, что a || b.

Так как ∠1 + ∠2 = °, это углы, значит || .

По условию || , согласно следствию 2 из аксиомы параллельных прямых || .

Доказательство

Выделите цветом правильный вариант ответа.

Что доказывает это утверждение?

Дано: прямая a, M не принадлежит прямой a.

Доказать: через точку, не лежащую на прямой, можно провести прямую, параллельную данной.

Через точку M проведем прямую c, перпендикулярную a.
Через точку M проведем прямую b перпендикулярную прямойc.
Так как a ┴ c, b ┴ c , то a ║b.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Аксиома параллельных прямых

Рассмотрим прямую a и точку M, не лежащую на этой прямой (Рис.1). Докажем, что через точку M можно провести прямую, параллельную прямой a.

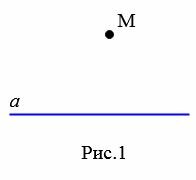Укажите следствия из аксиомы параллельных прямых

Проведем через точку M прямую c, перпендикулярно прямой a, и прямую b, перпендикулярно прямой c (Рис.2).

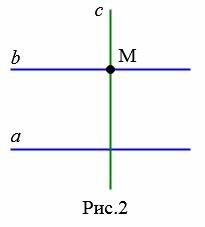Поскольку a и b перпендикулярны прямой с, то они параллельны (статья Перпендикулярные прямые Теорема 1 и статья Параллельные прямые. Признаки параллельности прямых Определение 1). Таким образом через точку M проходит прямая, параллельная прямой a.

Возникает вопрос, существует ли другая прямая, проходящая через точку M параллельно прямой a. Интуитивно ясно, что если немного повернуть прямую b вокруг оси M, то прямые b и a пересекутся. Но доказать это утверждение до сих пор не удалось. основываясь на стальных аксиомах геометрии.

Таким образом имеем это утверждение в виде аксиомы:

Аксиома 1. Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.

Следствие 1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

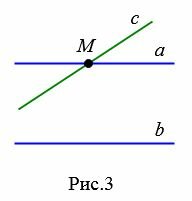Доказательство. Пусть заданы параллельные прямые a и b и пусть прямая c пересекает a в точке M (Рис.3). Докажем, что прямая c пересекает и прямую b.

Предположим обратное, т.е. c не пересекает b. Тогда получается, что через точку M проходят две прямые a и c параллельно прямой b, что невозможно (Аксиома 1). Следовательно прямая с пересекает и прямую b.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.

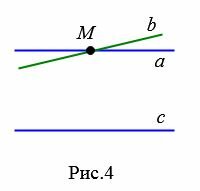Действительно. Предположим, что прямые a и b параллельны прямой c. Докажем, что прямая a параллельна прямой b. Предположим обратное, т.е. прямые a и b пересекаются в точке M (Рис.4). Тогда получается, что через точку M проходят две прямые, параллельные прямой c. Но это невозможно (Аксиома 1). Значит прямые a и b параллельны.

Видео:Следствия из аксиомы параллельных прямыхСкачать

Свойства параллельных прямых

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

С помощью данного видеоурока вы сможете самостоятельно изучить тему «Свойства параллельных прямых». В ходе него вам предстоит параллельные прямые, рассмотреть их свойства, а также сформулировать одну из самых важных аксиом геометрии.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»