В единичном кубе abcda1b1c1d1 найдите длину вектора ав ад

Видео:№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

Ваш ответ

Видео:егэ векторы решу егэ все задания №2 профильСкачать

Похожие вопросы

• Все категории
• экономические 43,280
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,971
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Подготовка к ЕГЭ

Разновидности стереометрических задач .

Просмотр содержимого документа
«Подготовка к ЕГЭ»

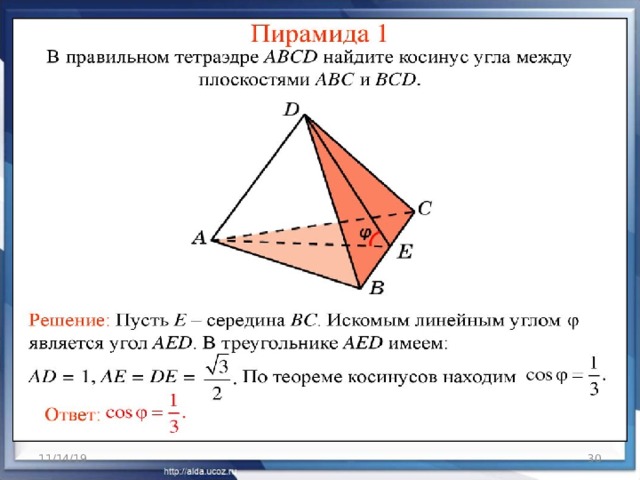
ПОДГОТОВКА К ЕГЭ. СТЕРЕОМЕТРИЧЕСКАЯ ЗАДАЧА(№14).

Работа учителя математики

Разновидности стереометрических задач.

• Расстояние от точки до прямой и до плоскости .
• Расстояние между прямыми и плоскостями .
• Угол между скрещивающимися прямыми .
• Угол между прямой и плоскостью .
• Угол между плоскостями .
• Задача на доказательство и вычисление .
• Сечения многогранников .
• Объёмы многогранников .
• Круглые тела: цилиндр, конус, шар.

Расстояние от точки до прямой.

• Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
• Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
• Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой .

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки D₁ до прямой PQ,

где P и Q – середины соответственно

В единичном кубе ABCDA ₁B₁C₁D₁ найти расстояние от точки С до прямой ВД1.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. АВ = 1. Найти: Расстояние от точки С до прямой ВД 1 .

1. ∆ВСД 1 – прямоугольный ( по теореме о трёх

перпендикулярах), ∠Д 1 СВ – прямой .

2. СН – высота ∆ВСД 1 , значит СВ – среднее

пропорциональное между ВН и ВД 1 , тогда

СН – расстояние от точки С до прямой ВД 1 , поэтому СН – высота треугольника ВСД 1 . СН = 2·S ∆ВСД 1 : ВД 1 .

∆ Д 1 СВ – прямоугольный, т.к. Д 1 С  СВ

по теореме о трёх перпендикулярах .

Расстояние от точки до плоскости .

• Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этого точки на плоскость.
• Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
• Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
• Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
• Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.

• В единичном кубе ABCDA₁B₁C₁D₁ найдите расстояние от точки C₁ до плоскости AB₁C.

• В правильной треугольной призме АВСА1В1С1–все рёбра равны 1.Найдите расстояние от точки А до плоскости (ВСА1)

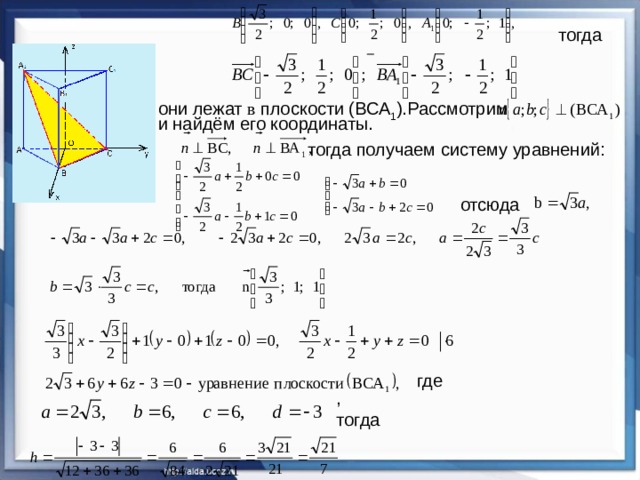
Дано: АВСА 1 В 1 С 1 – правильная треугольная призма, все рёбра равны 1. Найдите: Расстояние от точки А до плоскости (ВСА 1 )

Решение: h – расстояние от точки А до плоскости (ВСА 1 ),

поэтому h – высота пирамиды АВСА 1

с основанием ВСА 1 . h =

. Пусть основанием пирамиды будет ∆АВС,

тогда её высота – АА 1 .

∆ ВСА 1 – равнобедренный, А1К – его высота, тогда

За страницами учебника Расстояние от точки А до плоскости можно вычислить по формуле:

они лежат в плоскости (ВСА 1 ).Рассмотрим

и найдём его координаты.

тогда получаем систему уравнений:

Расстояние между прямыми и плоскостями .

• Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми. Общий перпендикуляр к двум скрещивающимся прямым существует и единственен.

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найти: расстояние между прямыми АВ 1 и ВС 1 .

следовательно расстояние между скрещивающимися

прямыми ВС 1 и АВ 1 равно расстоянию между

соответствующими плоскостями. Диагональ СА 1

перпендикулярна этим плоскостям.

СА 1 ∩ (ВДС 1 ) = F;

CА 1 ∩ (АД 1 В 1 ) = Е.

EF – расстояние между ВС 1 и АВ 1 .

В ∆ АСЕ отрезок ОF ║ АЕ и проходит через середину отрезка АС, следовательно ОF – средняя линия треугольника АСЕ и, значит, ЕF = FC. Аналогично, О 1 Е – средняя линия треугольника А 1 С 1 F

Расстояние между скрещивающимися прямыми можно найти по формуле:

Дано: АВСДА 1 В 1 С 1 Д 1 – куб. Все его рёбра равны 1. Найдите расстояние между прямыми АВ 1 и ВС 1 .

• SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1.Найдите расстояние между прямыми АS и ВС.

Дано: SABCD – правильная четырёхугольная пирамида, все рёбра которой равны 1. Найдите: Расстояние между прямыми АS и ВС.

Угол между прямой и плоскостью .

• Прямая и плоскость пересекаются , если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости .
• Прямая перпендикулярна к плоскости , если она перпендикулярна к любой прямой, лежащей в этой плоскости.
• Проекцией точкиМна плоскость называется либо сама точка М , если М лежит в плоскости , либо точка пересечения плоскости и прямой, перпендикулярной к плоскости и проходящей через точку М , если точка М не лежит в плоскости .
• Проекцией прямойaна плоскость называют множество проекций всех точек прямой a на плоскость .
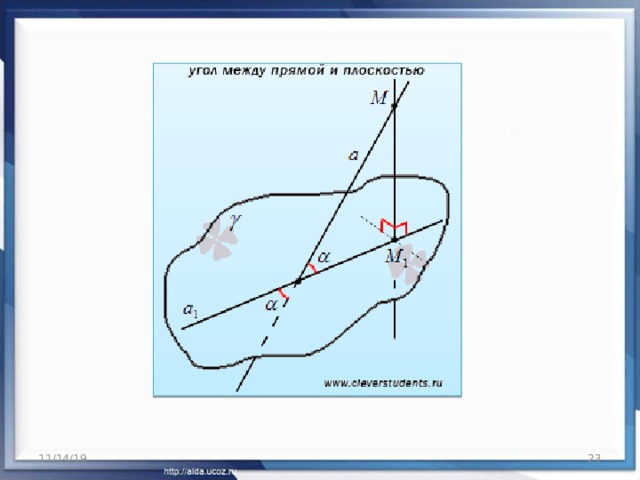
• Угол между прямой и плоскостью , пересекающей эту прямую и не перпендикулярной к ней, — это угол между прямой и ее проекцией на эту плоскость.
• Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми : самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.

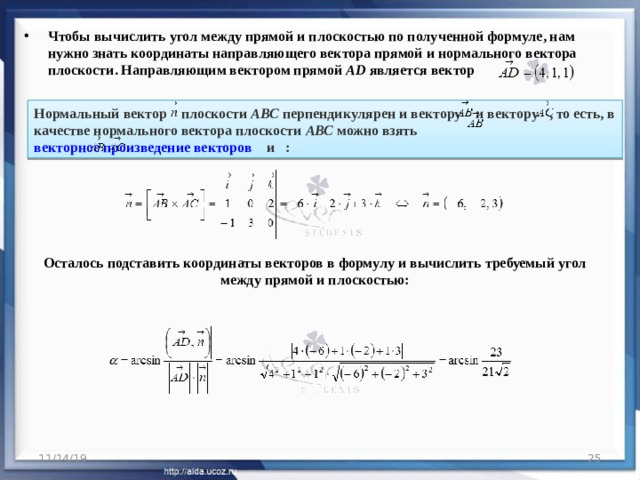
На векторах построена пирамида. Найдите угол между прямой AD и плоскостью ABC .

• На векторах построена пирамида. Найдите угол между прямойADи плоскостьюABC .

• Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямойADявляется вектор

Нормальный вектор плоскости АВС перпендикулярен и вектору и вектору , то есть, в качестве нормального вектора плоскости АВС можно взять векторное произведение векторов и :

Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:

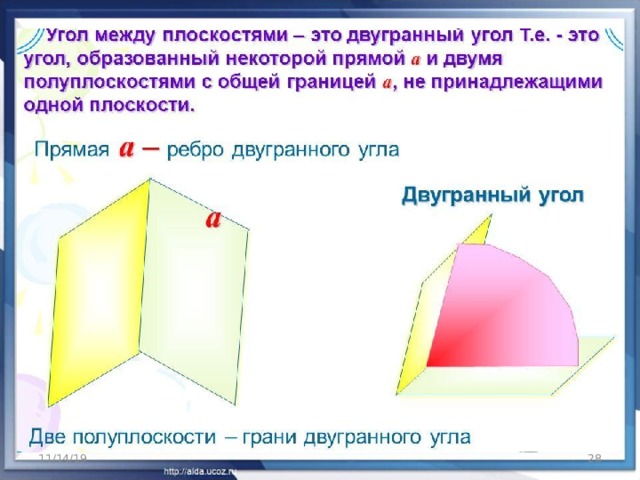
Угол между плоскостями .

Задача на доказательство и вычисление .

В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

В основании правильной треугольной призмы ABCA 1 B 1 C 1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A 1 C 1 .

а) Постройте сечение призмы плоскостью BAN .

б) Найдите периметр этого сечения.

См.сайт «Решу ЕГЭ»

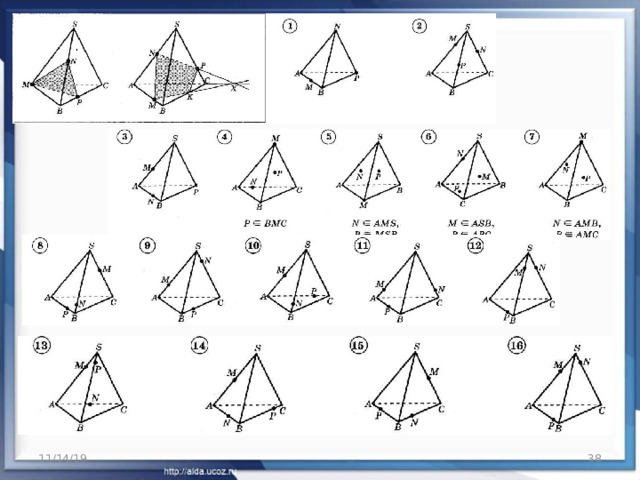
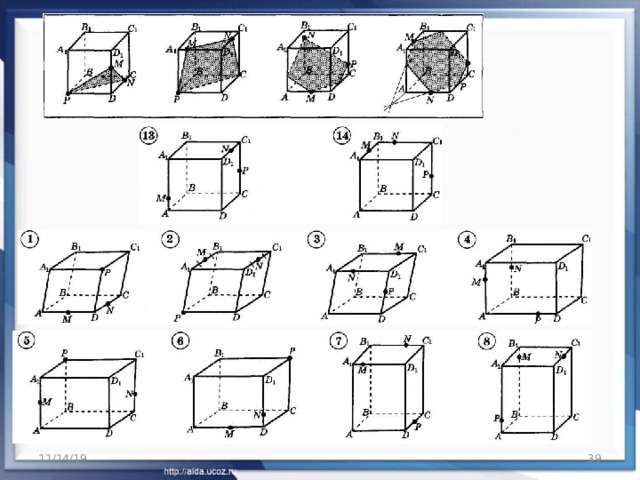
Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.

В задачах используются в основном простейшие многогранники.

Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

• что значит построить сечение многогранника плоскостью;
• как могут располагаться относительно друг друга многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

Метод следов. Метод вспомогательных сечений. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

• построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
• построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
• построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
• построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

• В правильной четырёхугольной пирамидеMABCDс вершинойMстороны основания равны 1, а боковые рёбра равны 2. ТочкаNпринадлежит ребруMC,причёмMN: NC = 2:1.Найдите площадь сечения пирамиды плоскостью, проходящей через точкиBиNпараллельно прямойAC.
• См . сайт «Решу ЕГЭ»

Видео:Задание 3 (№27717) ЕГЭ по математике. Урок 80Скачать

Геометрия. 10 класс

Сумма векторов

В кубе назовите вектор, равный сумме $overrightarrow+overrightarrow <B_C_>+overrightarrow<DD_> $

Вектор в пространстве

Установите соответствие между выражением и вектором $Х$

Длина вектора

Дано: АВ = 3 ВС = 4 СС₁ = 12

Длина вектора АС₁ =

Длина вектора

Диагонали параллелепипеда пересекаются в точке О.

Варианты ответа (введите порядковый номер):

Вектор в пространстве

Упростите выражение и выберите правильный результат преобразования:

Вектор в пространстве

В тетраэдре ABCD точка Е — середина АD.

Докажите, что $overrightarrow=frac(overrightarrow+overrightarrow)$

Сложим полученные равенства $overrightarrow+overrightarrow+overrightarrow+overrightarrow=2overrightarrow$

Так как $overrightarrow+overrightarrow=0$, то $overrightarrow+overrightarrow=2overrightarrow$, значит $overrightarrow=frac(overrightarrow+overrightarrow)$

🔥 Видео

КВАДРАТ ДЛИНЫ ВЕКТОРА ?/ Новое задание из ЕГЭ разбор #профиль #егэ #27731Скачать

Длина вектора через координаты. 9 класс.Скачать

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

вектор егэ. Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину вектора АССкачать

Угол между векторами | МатематикаСкачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 3, CD = 2, AD = 2. Найдите длинуСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

№745. В прямоугольнике ABCD AB=3см, BC=4см, M-середина стороны AB.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Полный разбор решения задачи №13 из ЕГЭ векторным методом. В единичном кубе ... найти длину отрезка.Скачать

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать