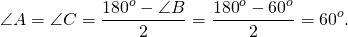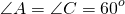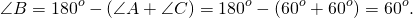Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
- Некоторые свойства прямоугольного треугольника:
- Соотношение между сторонами и углами в прямоугольном треугольнике:
- Значения тригонометрических функций некоторых углов:
- Особые свойства треугольника с углом 60 градусов
- Аннотация
- Ключевые слова
- Текст научной работы
- Читайте также
- Средства стохастической подготовки обучающихся на основе информационных технологий
- Инструментальная реализация прикладной математической подготовки бакалавра экономики и менеджмента
- Связность над распределением в главном расслоенном пространстве допустимых реперов
- Онтологические основания робототехники и образ мышления инженера XXI века
- Евклид и Архимед
- Список литературы
- Цитировать
- Поделиться
- Равнобедренный треугольник с углом 60 градусов
- 📸 Видео
Некоторые свойства прямоугольного треугольника:
1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$
7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
В прямоугольном треугольнике $АВС$ для острого угла $В$:
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Площадь прямоугольного треугольника равна половине произведения его катетов
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.
Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то
Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:
Катет $ВС$ мы можем найти по теореме Пифагора:
Подставим найденное значение в формулу косинуса
В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sinA=/, AC=9$. Найдите $АВ$.
Распишем синус угла $А$ по определению:
Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.
Применим теорему Пифагора, чтобы отыскать $«х»$
Так как длина $АВ$ составляет пять частей, то $3∙5=15$
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
Видео:Построить угол 60°Скачать

Особые свойства треугольника с углом 60 градусов
Калмыцкий государственный университет
NovaInfo32
Опубликовано 13 марта 2015
Раздел: Физико-математические науки
Просмотров за месяц: 485
CC BY-NC
Видео:В треугольнике АВС углы А и С равны 40 и 60 градусовСкачать

Аннотация
Треугольник с углом 60 градусов обладает необычными свойствами. Если этот треугольник не является правильным, то все три угла всегда образуют арифметическую прогрессию. Выполняется и обратное утверждение: Если сумма углов треугольника образует арифметическую прогрессию, то один из углов равен 60 градусам. Кроме того, между треугольниками с углами 45, 60, 75 и 30, 60, 90 градусов существует сложная взаимность.
Видео:№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

Ключевые слова
Видео:Соотношение сторон треугольника 30-60-90 (доказательство)Скачать
Текст научной работы
Докажем свойство треугольника с углом 60 градусов.
Теорема. Если треугольник с углом 60 градусов не является правильным, то его углы составляют арифметическую прогрессию.
Пусть в треугольнике ABC угол B равен 60 о , а угол A=α (рис.1). Так как сумма углов треугольника равна 180 о , то ÐA+ÐC=120 o . Тогда, ÐС=120 o −α.
Таким образом, ÐA=α, ÐB=60 o =α+(60 o −α), ÐC=120 o −α=α+2(60 o −α) (1)
Из соотношения (1) видно, что углы треугольника составляют арифметическую прогрессию с разностью 60 o −α. Теорема доказана.
Справедливо и обратное утверждение.
Теорема. Если углы треугольника составляют арифметическую прогрессию, то один из углов равен 60 о .
Пусть ÐA=α, ÐB=α+d, ÐC=α+2d (рис.2). Сумма углов треугольника равна 180 о , поэтому α+α+d+α+2d=180 o =>3α+3d=180 o =>α+d=60 o =>d=60 o −α.
Отсюда ÐB=α+60 o −α=60 o . Теорема доказана.
Существуют и другие необычные свойства треугольников с углами 60 о .
Для треугольника 45 о , 60 о , 75 о ортоцентрическим является треугольник с углами 30 о , 60 о , 90 о . Если продолжить высоты треугольника до их пересечения с описанной окружностью, то получим треугольник подобный высотному (рис.3).
Рисунок 3. Высотный треугольник и ему подобный
Назовём инцентрическим треугольник, образованный основаниями перпендикуляров опущенных из центра вписанной окружности на стороны. Для треугольника с углами 30 о , 60 о , 90 о инцентрическим будет треугольник с углами 45 о , 60 о , 75 о (рис.4).
Рисунок 4. Инцентрический треугольник
Видео:№225. Докажите, что каждый угол равностороннего треугольника равен 60°.Скачать

Читайте также
Средства стохастической подготовки обучающихся на основе информационных технологий
Инструментальная реализация прикладной математической подготовки бакалавра экономики и менеджмента
- Синчуков А.В.
NovaInfo59, с.24-28, 13 февраля 2017 , Физико-математические науки, CC BY-NC
Связность над распределением в главном расслоенном пространстве допустимых реперов
Онтологические основания робототехники и образ мышления инженера XXI века
- Волкова В.О.
- Волков И.Е.
- Гришагин М.В.
NovaInfo59, с.1-7, 8 февраля 2017 , Физико-математические науки, CC BY-NC
Евклид и Архимед
- Хазбулатов И.Р.
NovaInfo48, с.15-19, 29 июня 2016 , Физико-математические науки, CC BY-NC
Видео:Измерение угла с помощью транспортираСкачать

Список литературы
- Алгебра. 9 класс : учеб. для общеобразоват. организаций [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова] ; под ред. С. А. Теляковского. – 21-е изд. – М.: Просвещение, 2014. – 271 с.: ил.
- Геометрия: учеб. для 7-9 кл. сред. шк. /Л. С. Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1990. – 336 с.
Видео:№485. Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна с.Скачать

Цитировать
Баталаев, А.В. Особые свойства треугольника с углом 60 градусов / А.В. Баталаев. — Текст : электронный // NovaInfo, 2015. — № 32. — URL: https://novainfo.ru/article/3266 (дата обращения: 27.01.2022).
Видео:Построение углов заданной градусной мерыСкачать

Поделиться
Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.
Соучредители СМИ: Долганов А.А., Майоров Е.В.
Видео:Геометрия Синус.Чему равен синус 30,45,60 градусов?Вывод табличных значений.Скачать

Равнобедренный треугольник с углом 60 градусов
Если дан равнобедренный треугольник с углом 60 градусов, то что можно сказать об этом треугольнике?
Равнобедренный треугольник с углом 60 градусов является равносторонним.
Дано : ∆ ABC, AB=BC,
В равнобедренном треугольнике углы при основании равны: ∠A=∠C.
1) Если угол при вершине равнобедренного треугольника равен 60 градусов.
Таким образом, все углы треугольника равны: ∠A=∠B=∠C, следовательно треугольник ABC — равносторонний (по признаку).

(как углы при основании равнобедренного треугольника).
По теореме о сумме углов треугольника
Так как в треугольнике ABC все углы равны, то ABC — равносторонний (по признаку).
📸 Видео
Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Треугольники с углами 30, 60, 90 градусов. ВведениеСкачать

один из углов треугольника всегда не превышает 60 градусовСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Построение угла с помощью транспортираСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Геометрия, 10 класс | Треугольники с углами 60 и 120 градусов. Часть 1Скачать

ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА 30, 45 И 60 ГРАДУСОВСкачать
ОГЭ. Геометрия. 1 часть. Теорема синусов.Скачать

Построение угла с помощью транспортира. 5 клСкачать

Прямоугольный треугольник с углами "30°- 60°-90°".Скачать