В четырехугольнике авсд векторы ав и сд противоположные точка к середина сд прямая ак

Видео:№740. Начертите векторы АВ, CD, и EF так, чтобы:Скачать

Ваш ответ

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

решение вопроса

Видео:Угол между векторами. 9 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,754
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Урок изучения нового материала по теме «Векторы. Сумма векторов»

Презентации к уроку

Загрузить презентацию (255 кБ)

Загрузить презентацию (293 кБ)

Урок изучения нового материала по теме: «Векторы» (Презентация 1)

Главная дидактическая цель урока: Добиться умения самостоятельно формулировать определения понятий: вектор, длина вектора, коллинеарные и равные векторы каждым учащимся.

Цели урока:

• Показать изображение и обозначение вектора.
• Научить откладывать от любой точки пдоскости вектор, равный данному.
• Подготовить обучающихся к восприятию действий над векторными величинами.
• Воспитание коммуникативной культуры, приобретение опыта самостоятельной работы.
• Помочь учащимся осознать практическую и личную значимость учебного материала.

1. Организационный момент

2. Актуализация знаний

Многие физические величины характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (слайд 2)

3. Изучение нового материала

(слайд 3) Отвлекаясь от конкретных свойств физических векторных величин, мы приходим к геометрическому понятию вектора.
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая концом, называется направленным отрезком или вектором. Обозначение:
(слайд 4) Примеры векторов.
(слайд 5) Длиной или модулем ненулевого вектора называется длина отрезка АВ. Обозначение:
(слайд 6) Задача: Отметьте точки А, В и С, не лежащие на одной прямой. Начертите все ненулевые векторы, начало и конец которых совпадают с какими-то двумя из этих точек. Выпишите все полученные векторы и укажите начало и конец каждого вектора.
(слайд 7) Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.
Примеры: Векторы а и b; АВ и СД – сонаправленные. Векторы АВ и b – противоположно направленные.

(слайд 8) Векторы называются равными, если они сонаправлены и их длины равны.

Задачи:

1. (слайд 9) На рис. изображен параллелограмм АВСД. Укажите сонаправленные, противоположно направленные, равные векторы.

2. (слайд 10) На рис. изображена трапеция АВСД. Укажите сонаправленные, противоположно направленные, равные векторы.

3. (слайд 11) На рис. изображен треугольник АВС. Укажите сонаправленные, противоположно направленные, равные векторы.

(слайд 12) Откладывание вектора от данной точки: Если точка А – начало вектора а, то говорят, что вектор а отложен от точки А. Пример.

Задачи:

1. (слайд 13) Перечертите рисунок в тетрадь. Постройте векторы MN и KР такие, что MN = a, KP = a.

2. (слайд 14) Изобразите векторы АВ, СД, ОК, FE в системе координат, если известны координаты их начала и конца. Найдите длины векторов.

3. (слайд 15) В прямоугольнике АВСД АВ = 3 см, ВС = 4см, М – середина стороны АВ. Найдите длины векторов:

4. Самостоятельная работа

5. Итог урока

Урок изучения нового материала по теме: «Сумма векторов» (Презентация 2)

Главная дидактическая цель урока: добиться умения самостоятельно выполнять сложение векторов каждым учащимся.

Цели урока:

• Ввести понятие суммы двух векторов.
• Познакомить с правилами сложения векторов.
• Рассмотреть законы сложения векторов.
• Воспитание коммуникативной культуры, приобретение опыта самостоятельной работы.
• Помочь учащимся осознать практическую и личную значимость учебного материала.

1. Организационный момент

2. Актуализация знаний

(слайд 2) Устный опрос:

1. Дайте определение вектора. Объясните, какой вектор называется нулевым.
2. Что называется длиной ненулевого вектора?
3. Какие векторы называются коллинеарными?
4. Дайте определение равных векторов.

3. Решение задач:

(слайд 3) №1. Дан параллелограмм АВСД с диагоналями, пересекающимися в точке О. Отметьте векторы: . Запишите: равные векторы, противоположные векторы.

(слайд 4) №2. Дано: АВСД – четырехугольник, АВ = ДС. Доказать, что АВСД – параллелограмм.

№3. В четырехугольнике АВСД ВС АД, ВС = 3, АД = 5. Изобразите этот четырехугольник. Как он называется?

4. Изучение нового материала

(слайд 5) Пример – перемещение точки. Результат перемещения можно представить вектором. Рассмотренный пример приводит к понятию суммы двух векторов. Полученный вектор называется – суммой векторов.

(слайд 6) Сумма векторов: последовательное отложение векторов, когда конец первого вектора совмещается с началом второго, и вектор, имеющий начало в начале первого, а конец в конце второго будет вектором-суммой данных векторов.

(слайд 7) Правило треугольника.

(слайд 8) Задача: Найти равнодействующую двух сил , приложенных к материальной точке А.

От одной точки откладываются векторы, равные данным. На векторах, как на сторонах строится параллелограмм и из общего начала векторов проводится диагональ. Вектор, совпадающий с диагональю – вектор-сумма векторов.

(слайд 9) Правило параллелограмма.

(слайд 10) Пример сложения двух векторов по правилам треугольника и параллелограмма. (Демонстрация на слайде выполняется последовательно. Показать обучающимся, что в результате получаются равные векторы.)

(слайд 11) Правило многоугольника. Демонстрация на слайде.

(слайд 12) Задача:

Сторона равностороннего треугольника АВС равна а. Найдите:

(слайд 13) Законы сложения векторов:

1. Переместительный закон:

2. Сочетательный закон:

(слайд 14) Пример: Упростить выражения:

(слайд 15) Задача:

Докажите, что если А, В, С и Д – произвольные точки, то

5. Математический диктант

6. Итог урока

Используемая литература:

1. Л.С.Атанасян, В.Ф.Бутузов и др. Геометрия, 7-9: учебник для общеобразоват. Учреждений – М.: Просвещение, 2006.
2. Л.С.Атанасян, В.Ф.Бутузов и др. Изучение геометрии в 7, 8, 9 классах: Методические рекомендации к учебнику – М. Просвещение, 2003.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

В ЧЕТЫРЁХУГОЛЬНИКЕ ABCD ВЕКТОРЫ AB И CD ПРОТИВОПОЛОЖНЫЕ. ТОЧКА К СЕРЕДИНА CD ПРЯМАЯ АК ПЕРЕСЕКАЕТ ПРЯМУЮ BC В ТОЧКЕ M. КАКИЕ ВЕКТОРЫ БУДУ: СОНАПРАВЛЕННЫМИ (2 ШТ):
ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫМИ: AD, (И ЕЩЁ 3 ШТ)
РАВНЫЕ (2 ШТ):
ВЕКТОРЫ, ИМЕЮЩИЕ РАВНЫЕ ДЛИНЫ: KM, (И ЕЩЁ 3 ШТ)

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Ответы на вопрос

120 = 1/3 c = 1/3 * 6п = 2 п — длина дуги в 120 градусов теперь из дуги делаем окружность = > 2 п = 2п r = > r =1

отношение площадей подобных фигур равно квадрату коэффициента подобия значит в нашем случае коэффициент подобия равен 2,тогда соответствующая сторона равна 5*2=10

для начала построй парал-пед,затем проведи диагональ (допустима1с(а1 в основании))и проведи диагональ в основании(в нашем случае а1с1).угол между этими диагоналями и есть45гр.т.к. пар-пед прямоугольный то угол а1с1с=90гр.,сл. сс1=а1с1.найдем а1с1(по теореме пифагора)а1с1=8^2+6^2(под корнем)=100(под корнем)=10,сл.сс1=10.тогда v=10*8*6=480см.кв.

дано: sabcd-правильная пирамида

найти: сторону основания пирамиды.

авсd-правильная пирамида, следовательно, в её основании лежит правильный многоугольник, т.е. квадрат.

рассмотрим треугольник som, в нём so-высота пирамиды, следовательно so перпендикулярно основанию.

по теореме пифагора ом=sqr(sm^2-so^2)=sqr(6^2-(3sqr(2))^2)=

🎬 Видео

№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать

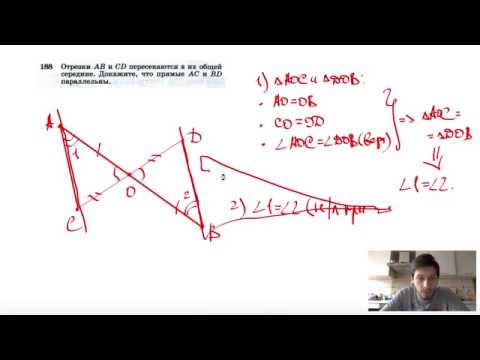
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

№783. Точка М лежит на стороне ВС параллелограмма ABCD, причем ВМ:МС=3:1. ВыразитеСкачать

№ 401-500 - Геометрия 9 класс МерзлякСкачать

№745. В прямоугольнике ABCD AB=3см, BC=4см, M-середина стороны AB.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

9 класс. Контрольная №1 (из 6). Тема: Векторы. Подробное решение с объяснением. Пробуем свои силы!Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№751. Определите вид четырехугольника ABCD, если:Скачать

№748. Диагонали параллелограмма ABCD пересекаются в точке O. Равны ли векторы?Скачать

Скалярное произведение векторов. 9 класс.Скачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать