В четырехугольнике авсд точки м и к середины сторон вс и ад соответственно

Видео:№320. В тетраэдре ABCD точки М, N и К— середины ребер АС. ВС и CD соответственноСкачать

Ваш ответ

Видео:Геометрия Точки M и K – соответственно середины сторон AB и BC ромба ABCD. Докажите, что MD = KDСкачать

решение вопроса

Видео:Геометрия Точки M, N, K и P – середины сторон AB, BC, CD и AD параллелограмма ABCD соответственноСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,742
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:В треугольнике ABC на сторонах АВ и ВС отмечены точки М и К соответственно, ВМ/АВ = 1/2, ВК/ВС = 4/5Скачать

В параллелограмме АВСD точки M и К — середины сторон ВС и АD соответственно?

Геометрия | 5 — 9 классы

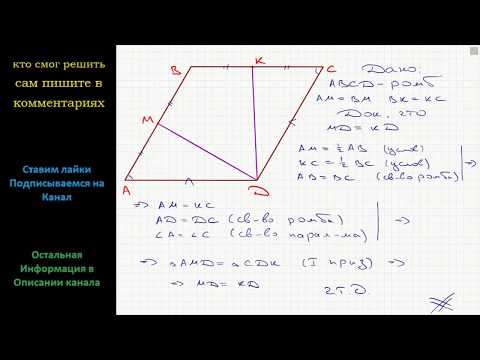
В параллелограмме АВСD точки M и К — середины сторон ВС и АD соответственно.

Докажите, что площадь четырехугольника АВМК равна площади треугольника АСD.

из этих равенств следует что АВСД = МКСД

это же элементарно, ватсон)) хех.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В прямоугольнике АВСD диагонали пресекаются в точке О, а Р и F — середины сторон DC и AD соответственно?

В прямоугольнике АВСD диагонали пресекаются в точке О, а Р и F — середины сторон DC и AD соответственно.

Докажите, что четырехугольник FOCP является параллелограммом.

Видео:№785. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD.Скачать

На стороне ВС параллелограмма АВСD отметили точку М Найдите площадь параллелограмма ABCD , если площадь треугольника MAD — 21?

На стороне ВС параллелограмма АВСD отметили точку М Найдите площадь параллелограмма ABCD , если площадь треугольника MAD — 21.

Видео:9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

В треугольнике АВС отмечины середины М и N сторон ВС и АС соответственно площадь треугольника CNM равна 89 найдите площадь четырехугольника АВМN?

В треугольнике АВС отмечины середины М и N сторон ВС и АС соответственно площадь треугольника CNM равна 89 найдите площадь четырехугольника АВМN.

Видео:Геометрия Точки E и F – соответственно середины сторон BC и AD параллелограмма ABCD. Докажите, чтоСкачать

Площадь параллелограмма АВСД равна 60?

Площадь параллелограмма АВСД равна 60.

Точка Е — середина стороны СД.

Найдите площадь треугольника АДЕ.

Видео:Ященко. ЕГЭ. Профильная математика. 1 вариант. 2023. 13 задание. GeoGebra.Скачать

На стороне АВ параллелограмма АВСD проведена произвольная точка G?

На стороне АВ параллелограмма АВСD проведена произвольная точка G.

Докажите, что сумма площадей треугольников ACG и BGD равна половине площади параллелограмма.

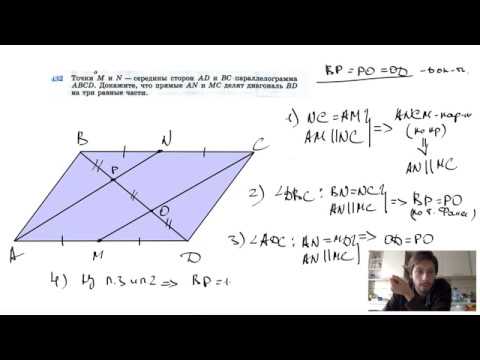
Видео:№432. Точки М и N — середины сторон AD и ВС параллелограмма ABCD. Докажите, что прямыеСкачать

Площадь трапеции АВСЕ равна 33?

Площадь трапеции АВСЕ равна 33.

Точка Е — середина стороны СD найдите площадь параллелограмма АВСD.

Видео:Красивая задача №3 из ЕГЭ-2022. Параллелограмм Вариньона |ЕГЭ по математике профильного уровняСкачать

В выпуклом четырехугольнике АВСD отмечены точки K, L, M и N — середины сторон AD, AB, BC, и CD соответственно?

В выпуклом четырехугольнике АВСD отмечены точки K, L, M и N — середины сторон AD, AB, BC, и CD соответственно.

Найдите отношение площади четырехугольника АВСD к площади четырехугольника KLMN.

Видео:№346. Точки М и N — середины оснований АВ и CD трапеции ABCD, а О — произвольнаяСкачать

В треугольнике АВС отмечены середины М и N сторон ВС и АС соответственно?

В треугольнике АВС отмечены середины М и N сторон ВС и АС соответственно.

Площадь треугольника CNM равна 2.

Найдите площадь четырехугольника ABMN.

Видео:Геометрия Точки E и K — соответственно середины сторон CD и AD квадрата ABCD. Прямая BE пересекаетсяСкачать

В треугольнике ABC отмечены середины M и N сторона BC и AC соответственно?

В треугольнике ABC отмечены середины M и N сторона BC и AC соответственно.

Площадь треугольника CNM равна 2.

Найдите площадь четырехугольника ABMN?

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

В параллелограмме АВСD точка E — середина стороны ВС, а F — середина стороны АD?

В параллелограмме АВСD точка E — середина стороны ВС, а F — середина стороны АD.

Докажите, что четырехеугольник BEDF — параллелограмм.

На этой странице сайта вы найдете ответы на вопрос В параллелограмме АВСD точки M и К — середины сторон ВС и АD соответственно?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Нехай, кути трикутника будуть 3х, 7х і 120° Тоді, 3х + 7х + 120° = 180° 10х = 180 — 120 10х = 60 х = 60 / 10 х = 6 отже, перший кут х = 6 * 3 = 18° ; другий кут х = 6 * 7 = 42° відповідь : 18°, 42°, 120°.

1) по условию АВ параллельно CD, BC параллельно AD следовательно ABCD — параллелограмм(по второму признаку). 2) АС пересекает BD в точке О, значит AO = OC BO = OD(по второму свойству параллелограмма)AC = AO + OC = 16 см, тогда АО = 8смBD = BO + OD =..

В ранобедренном треугольнике боковые стороны равны. AB = BC = 12 cм Прямая параллельная какой либо стороне треугольника отсекает от него треугольник подобный данному. MN II AC⇒ Треугольник BMN подобен треугольнику BAC (по трем углам)⇒ Сходственные ..

39 СЕД равнобедренный. Высота и биссектриса это одно и то же.

Высота призмы (раз уж она прямая)равна длине диагонали умноженной на синус 30 градусов, то есть 12 * 0. 5 = 6.

Вроде бы вот так : )).

1)1 2)1 3)отрезок это часть прямой имеющий начало и конец 4)луч это часть прямой имеющий начало но не имеющий конца 5)угол геометрическая фигура которая состоит из двух лучей исходящих из одной точки 6)угол который равен 180 градусам 7)равные если их..

Пусть один угол х, тогда другой 20 + х, получим х + 20 + х = 180 2х = 160 х = 80 — один угол 20 + х = 20 + 80 = 100 — другой угол.

Пусть O — точка пересечения диагоналей AC и BD — начало координат Ось X — OA Ось Y — OB Ось Z — OO1 Координаты точек A(3 ; 0 ; 0) B1(0 ; 6 ; √15) D1(0 ; — 6 ; √15) C( — 3 ; 0 ; 0) Направляющий вектор AB1( — 3 ; 6 ; √15) Направляющий вектор D1C( — 3 ;..

Видео:Геометрия Точки M и K – середины сторон AB и AC треугольника ABC соответственно. Найдите периметрСкачать

В четырехугольнике авсд точки м и к середины сторон вс и ад соответственно

Вариант 1

1. В четырехугольнике ABCD: АВ || CD, ВС || AD, АС = 20 см, BD = 10 см, АВ = 13 см. Диагонали четырехугольника ABCD пересекаются в точке О. Найдите периметр Δ COD.
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр ВК к прямой AD; ВК = АВ : 2. Найдите ∠C, ∠D.
3. Середина отрезка BD является центром окружности с диаметром АС, причем точки А, В, С, D не лежат на одной прямой. Докажите, что ABCD – параллелограмм.

Вариант 2

1. В четырехугольнике ABCD АВ || CD, ВС || AD, О – точка пересечения диагоналей. Периметр Δ AOD равен 25 см, АС = 16 см, BD = 14 см. Найдите ВС.
2. В параллелограмме ABCD с острым углом А из вершины В опущен перпендикуляр ВК к прямой AD, AK = ВК. Найдите ∠C, ∠D.
3. Дан параллелограмм ABCD. На продолжении диагонали АС за вершины А и С отмечены точки М и N соответственно так, что AM = CN. Докажите, что MBND – параллелограмм.

II уровень сложности (задания)

Вариант 3

1. В четырехугольнике ABCD ∠А + ∠B = 180°, АВ || CD. На сторонах ВС и AD отмечены точки М и К соответственно так, что ВМ = KD. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
2. На сторонах РК и МН параллелограмма МРКН взяты точки А и В, соответственно МР = РВ = АК; ∠MPB = 60°. Найдите углы параллелограмма и сравните отрезки ВМ и АН.
3. На основании АС равнобедренного треугольника АВС отмечена точка К, а на сторонах АВ и ВС – точки М и Р соответственно, причем РК = MB, ∠KPC = 80°, ∠C = 50°. Докажите, что КМВР – параллелограмм.

Вариант 4

1. В четырехугольнике МРКН ∠PMK = ∠HKM, РК || МН. Через точку пересечения диагоналей проведена прямая, пересекающая стороны РК и МН в точках А и В соответственно. Докажите, что АР = НВ.
2. На сторонах ВС и AD параллелограмма ABCD взяты точки М и К, АВ = ВМ = KD, ∠AMB = 30°. Найдите угол параллелограмма и сравните отрезки АМ и СК.
3. В треугольнике МРК ∠M = 65°. На сторонах МК, МР, РК отмечены точки А, В, С соответственно так, что середина стороны РК – точка С, AM = КС, BP = АС, ∠BAM = 50°. Докажите, что ВРСА – параллелограмм.

III уровень сложности (задания)

Вариант 5

1. В выпуклом четырехугольнике ABCD ∠A + ∠B = ∠B + ∠C = = 180°. Через точку О пересечения диагоналей четырехугольника проведена прямая, пересекающая стороны ВС и AD в точках М и К соответственно; ∠BOM = 90°. Докажите, что KD = ВМ.
2. На сторонах ВС и CD параллелограмма ABCD отмечены точки М и Н соответственно так, что отрезки ВН и MD пересекаются в точке О; ∠BHD = 95°, ∠DMC = 90°, ∠BOD = 155°. Найдите отношение длин отрезков АВ и MD и углы параллелограмма.
3. Точки М и К являются соответственно серединами сторон АВ и ВС треугольника АВС. Через вершину С вне треугольника проведена прямая, параллельная АВ и пересекающая луч МК в точке Е. Докажите, что КЕ = АС : 2.

Вариант 6

1. В выпуклом четырехугольнике МРКН ∠M + ∠P = 180°, ∠MKH = ∠KMP. На сторонах МН и РК отмечены точки А и В так, что РВ = РА. Отрезок АВ проходит через точку пересечения диагоналей четырехугольника. Докажите, что HP ⊥ АВ.
2. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О; ∠BOD = 140°, ∠DKB = 110°, ∠BMC = 90°. Найдите отношение длин отрезков МС и AD и углы параллелограмма.
3. Точки А и В принадлежат соответственно сторонам РЕ и ЕТ треугольника РЕТ. Прямая, проходящая через вершину Т вне треугольника, пересекает луч АВ в точке К так, что АР = КТ, АВ = ВК= РТ : 2. Докажите, что точка А является серединой отрезка РЕ.

Геометрия 8 Атанасян Самостоятельная 2. ОТВЕТЫ

I уровень сложности (ответы)

Вариант 1

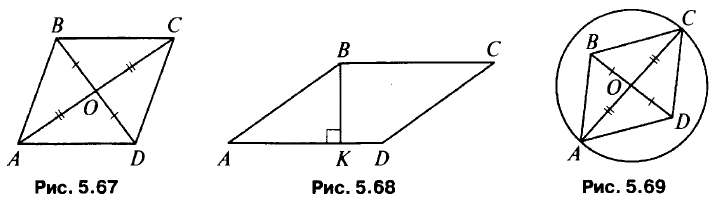
1. ABCD – параллелограмм (рис. 5.67), тогда CD = АВ = 13 см, ОС = АО = 10 см, BD = OD = 5 см (объясните). P_COD = 10 + 5 + 13 = 28 см.
2. ВК = АВ/2 (рис. 5.68), тогда ∠A = 30° (объясните), значит, ∠C = 30°, ∠D = 150° (объясните).
3. В четырехугольнике ABCD (рис. 5.69) середину отрезка BD отметим точкой О. Отсюда следует, что BO = OD.
   Одновременно точка О является центром окружности с диагональю AC, следовательно AO = OC.
   По свойству параллелограммов (диагонали пересекаются и точкой пересечения делятся пополам), если BO = OD и AO = OC, то ABCD – параллелограмм.

Вариант 2

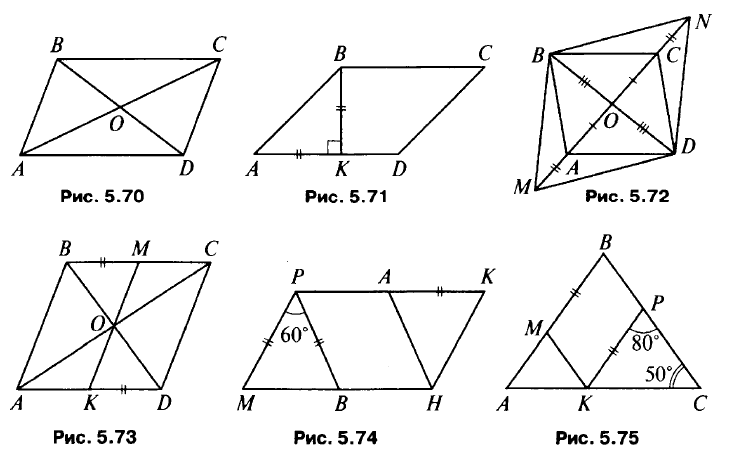
1. ABCD – параллелограмм (рис. 5.70), тогда АО = СО = 8 см, ВО = DO = 7 см (объясните). Так как P_AOD = 25 см, то ВС = AD = 10 см.
2. AK = ВК (рис. 5.71), тогда ∠A = 45° (объясните), ∠C = 45°, ∠D = 135° (объясните).
3. ABCD – параллелограмм (рис. 5.72), тогда АО = СО, ВО = DO. В четырехугольнике MBND диагонали точкой пересечения делятся пополам, значит, MBND – параллелограмм.

II уровень сложности (ответы)

Вариант 1

1. (рис. 5.73) а) Докажите, что ABCD – параллелограмм и ВС || AD. б) Докажите, что ΔBOM = ΔDOK и ОМ = ОК.
2. (рис. 5.74) а) Докажите, что ΔМРВ – равносторонний, ∠M = 60°, ∠K = 60. б) Докажите, что ΔАКН – равносторонний, ΔАКН = ΔМРВ, тогда МВ = АН, ∠M = ∠K = 60°, ∠P = ∠H = 120°.
3. (рис. 5.75) а) Найдите ∠B и докажите, что МВ || КР. б) Докажите, что МВРК – параллелограмм.

Вариант 2

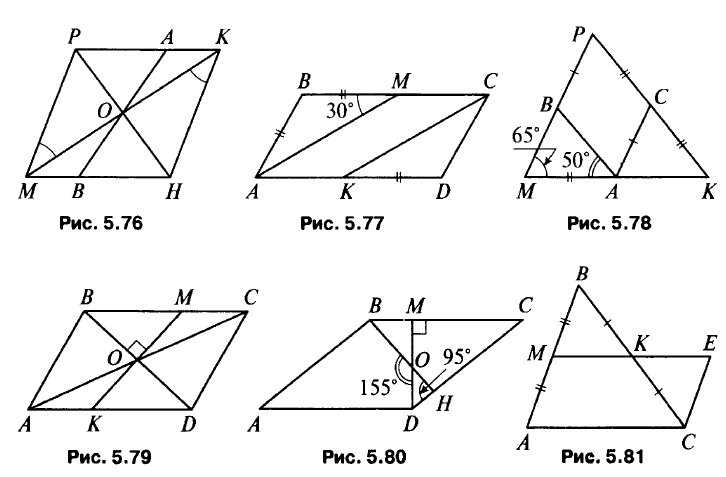
1. (рис. 5.76) а) Докажите, что МРКН – параллелограмм и РО = НО. б) Докажите, что ΔРОА = ΔНОВ и РА = НВ.
2. (рис. 5.77) а) Докажите, что ΔАВМ – равнобедренный, ∠B = 120°, ∠BAD = 60°. б) Докажите, что ΔАВМ = ΔKDC и AM = КС, ∠B = ∠D = 120°, ∠14 = ∠C = 60°.
3. (рис. 5.78.) а) Докажите, что в ΔАВМ МА = ВА. б) Докажите, что ВРСА – параллелограмм.

III уровень сложности (ответы)

Вариант 1

1. (рис. 5.79) а) Докажите, что ΔBCD – параллелограмм и АО = СО. б) Докажите, что ΔАОК = ΔСОМ и КО = МО. в) Докажите, что ΔDKO = ΔВМО и KD = ВМ.
2. (рис. 5.80) ∠MDC = 60°, ∠MCD = 30° (объясните). MD = CD/2, AB : MD = 2 : 1, ∠C = ∠A = 30°, ∠B = ∠D = 150°.
3. (рис. 5.81) а) Докажите, что ΔMВК = ΔЕСК и ЕС = МВ = AM, КЕ = МК = ME/2; б) Докажите, что АМЕС – параллелограмм и ME = АС, т. е. КЕ = АС/2.

Вариант 2

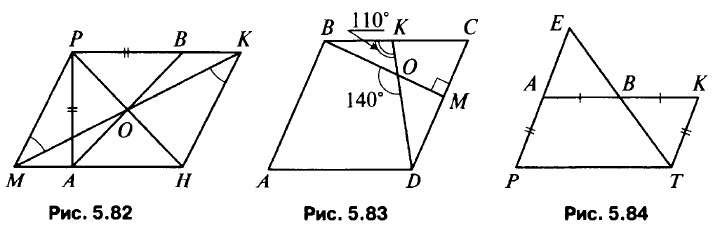
1. (рис. 5.82) а) Докажите, что МРКН – параллелограмм и МО = ОК. б) Докажите, что ΔMОА = ΔКОВ и АО = ОВ. в) Докажите, что РО⊥АВ и PH⊥АВ.
2. (рис. 5.83) ∠KDC = 50°, ∠MCB = 60°, ∠CBM = 30° (объясните). СМ = ВС/2; МС : AD = 1 : 2; ∠C = ∠A = 60°, ∠B = ∠D = 120°.
3. (рис. 5.84) а) Докажите, что РАКТ – параллелограмм и РЕ || КТ. б) Докажите, что ΔАЕВ = ΔКТВ и АЕ = КТ = РА, т. е. А – середина РЕ.

Вы смотрели: Геометрия 8 класс (УМК Атанасян и др. — Просвещение). Урок 4. Самостоятельная работа № 2 «Параллелограмм» с ответами (3 уровня сложности по 2 варианта в каждом). Геометрия 8 Атанасян Самостоятельная 2. Ориентировано на работу с базовым учебником: «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение». В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО».

💡 Видео

4.44.1. Планиметрия. Гордин Р.К.Скачать

Геометрия Точки E и F – соответственно середины сторон BC и CD ромба ABCD. Докажите, что угол EACСкачать

Самое сложное задание из досрочного ЕГЭ 2019Скачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

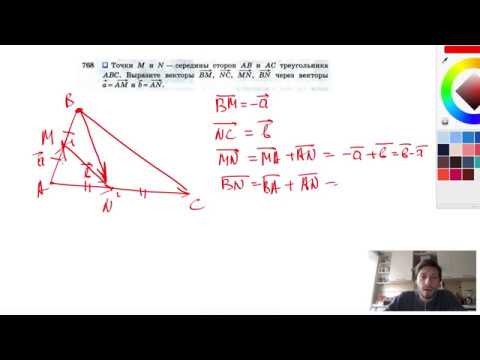
№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать