Впишите правильный ответ.
В четырёхугольник ABCD вписана окружность. Точки касания этой окружности со сторонами
делят стороны на отрезки как показано на рисунке. Найдите периметр четырёхугольника, если LC = 6, BK = 2, AN = 4, ND = 5.
Впишите правильный ответ.
Точки A, B и D делят окружность на три части так, что градусная мера дуги AB равна 160°, а градусные меры дуг AD и DB относятся как 3 к 2. Найдите градусную меру дуги DB.
Впишите правильный ответ.
Найдите площадь равнобедренного треугольника, вписанного в окружность радиуса 17 см и высотой, проведённой к основанию, равной 25 см. Ответ дайте в квадратных сантиметрах.
Выберите правильный ответ.
Известно, что ∠ABD = 50°, ∠BDC = 20°. Найдите угол BPC. Ответ дайте в градусах.
Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

В четырехугольник авсд вписана окружность известно что точка касания делит стороны
Задание 6. В четырёхугольник ABCD вписана окружность, АВ = 8 , ВС = 4 и CD = 25. Найдите четвёртую сторону четырёхугольника.
Так как в четырехугольник вписана окружность, то он обладает свойством, что сумма его противоположных сторон равна, т.е.
Найдем сторону AD из этого равенства, получим
Видео:ЕГЭ Математика Задание 6#27935Скачать

Окружность, вписанная в четырехугольник
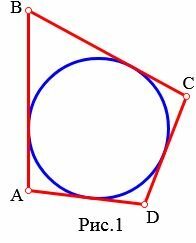
Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.
На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.
 |
Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.
Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).
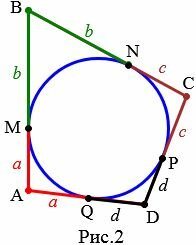 |
Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то
| ( small AM=AQ=a, ) ( small BM=BN=b, ) ( small CN=CP=c, ) ( small DQ=DP=d ) |
| ( small AB+CD ) ( small=AM+BM+CP+DP ) ( small =a+b+c+d, ) | (1) |
| ( small AD+BC) ( small=AQ+DQ+BN+CN) ( small=a+d+b+c. ) | (2) |
Из равенств (1) и (2), следует:
( small AB+CD=AD+BC. )  |
Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
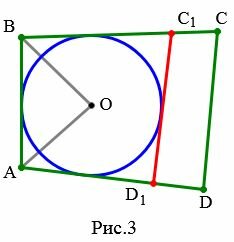
Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.
 |
Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.
Пусть эта окружность не касается стороны CD. Тогда возможны два случая.
Случай 1. Сторона CD не имеет общих точек с построенной окружностью.
Проведем касательную C1D1 к окружности, параллельно стороне CD четырехугольника.
Тогда окружность с центром O вписан в четырехугольник ABC1D1. Следовательно, по теореме 1, имеем:
| ( small AB+C_1D_1=AD_1+BC_1. ) | (3) |
Но по условию данной теоремы:
| ( small AB+CD=AD+BC. ) | (4) |
Вычтем из равенства (4) равенство (3):
| ( small CD-C_1D_1) (small=AD-AD_1+BC-BC_1 ) |
| ( small CD-C_1D_1=DD_1+CC_1 ) |
| ( small CD=DD_1+CC_1+C_1D_1) |
Получили, что в четырехугольнике CC1D1D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).
Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.
Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).
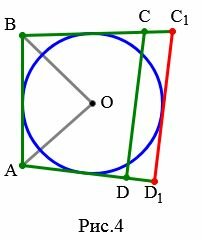 |
Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.
Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.
Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.
📸 Видео
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Геометрия В прямоугольную трапецию вписана окружность. Точка касания делит большую боковую сторонуСкачать

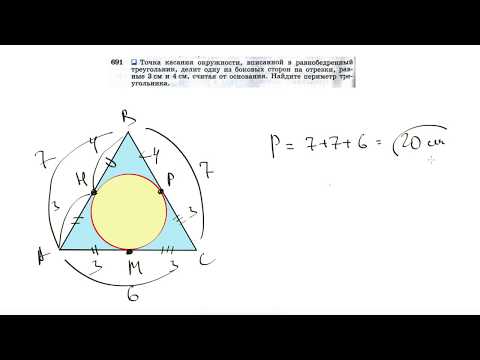
№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
3 правила для вписанного четырехугольника #shortsСкачать

2122 в четырёхугольник ABCD вписана окружность AB равно 17 CD равно 22Скачать

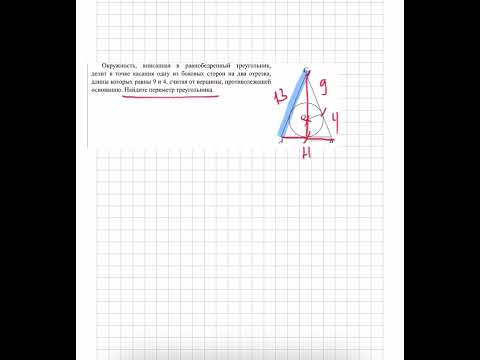
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторонСкачать
Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

🔴 В угол C, равный 165°, вписана окружность с ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

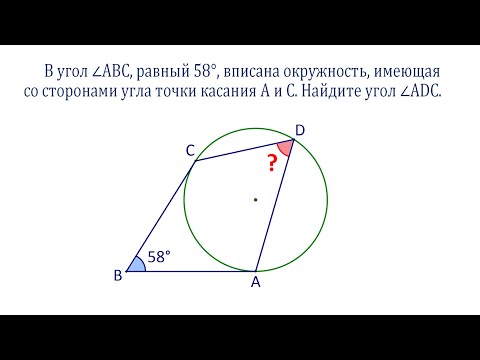
В угол вписана окружность, найдите вписанный угол этой окружностиСкачать
Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

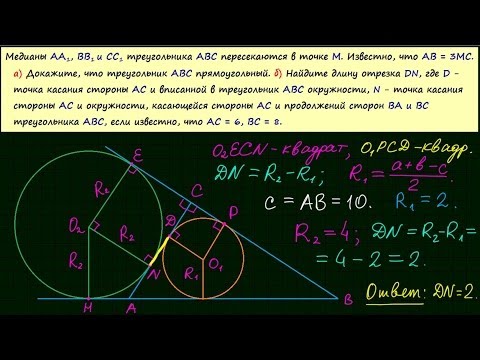
Задача 16. ЕГЭ по математике-1Скачать
Всё про углы в окружности. Геометрия | МатематикаСкачать

Разбор ВСЕХ прототипов задания 1 ЕГЭ по профильной математикеСкачать

Геометрия Точка касания окружности, вписанной в прямоугольную трапецию, делит ее меньшее основаниеСкачать
2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать



