Четырехугольники, как частный случай многоугольников, очень важная тема, изучаемая в школьном курсе геометрии. Современная программа подразумевает ознакомление с этим материалом в восьмом классе. В рамках школьного обучения рассматриваются исключительно выпуклые четырехугольники. Остальные же изучаются на уровне высших учебных заведений.
Изучение четырехугольников происходит в разных программах изучения геометрии неодинаково. Порядок введения понятия зависит от последовательности подачи материала о многоугольниках.
- Порядок изучения четырехугольников
- Классификация фигур с четырьмя углами
- Четырехугольники, называемые выпуклыми
- Обычный параллелограмм
- Прямоугольник
- Квадрат
- Трапеция
- Общие выводы по теме
- Разница между квадратом и прямоугольником
- Определение
- Сравнение
- Чем отличается прямоугольник от четырехугольника
- Ход урока
- Признаки и свойства прямоугольника
- Формулы для вычисления длины сторон
- Периметр и площадь
- Диагонали прямоугольника
- Определение и свойства квадрата
- Примеры вопросов и задач
- Определение
- Сравнение
- 🎥 Видео
Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Порядок изучения четырехугольников
В одном случае четырехугольник рассматривается как частный случай многоугольника, в другом — определяется как совокупность отрезков и точек, расположенных на их пересечении, числом по четыре. При этом должны выполняться условия непринадлежности любых из трех этих точек одной прямой, и отсутствия пересечений, кроме как в вершинах.
В большинстве школ Четырехугольники изучаются в восьмом классе. Изучив сначала параллельность прямых, затем теорему о сумме углов многоугольника, переходят к параллелограмму. Рассмотрев его признаки и доказав связанные с ними теоремы, переходят к остальным частным случаям, получая ответы на вопросы: какой четырехугольник называется квадратом, ромбом, прямоугольником и различными видами трапеций.

Еще один подход — изучение четырехугольников при рассмотрении темы подобных фигур. Здесь также последовательно изучаются четырехугольники начиная с параллелограмма. Определяется – какой четырехугольник называется прямоугольником, трапецией. И конечно, подробно рассматривается, какими фигурами могут быть остальные четырехугольники.
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Классификация фигур с четырьмя углами
Какой четырехугольник называется квадратом? Выяснить это можно, изучив все фигуры, имеющие отношения к данной по порядку. Первым в наше внимание попадет объект, называемый параллелограммом. Он образуется четырьмя прямыми попарно параллельными и пересекающимися. Отдельно определяются случаи, когда это происходит под углами в девяносто градусов и те, в которых все отрезки, образованные таким пересечениями, имеют одну длину. В завершение, выясним, какой четырехугольник называется трапецией.
Видео:Прямоугольник. Что такое прямоугольник?Скачать

Четырехугольники, называемые выпуклыми
Остановимся на понятиях выпуклых, а также невыпуклых четырехугольников. Данное различие имеет большое значение, так как в школьной программе изучаются только первые из них.
Какой четырехугольник называется выпуклым? Для того чтобы разобраться в этом последовательно, проведем через все стороны фигуры прямые линии. Если во всех случаях весь четырехугольник лежит в одной из двух полуплоскостей образованных этой прямой – он выпуклый. В противном случае, соответственно, невыпуклый.
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Обычный параллелограмм
Теперь рассмотрим основные виды выпуклых четырехугольников. Начнем с параллелограмма. Выше мы приводили определение этой фигуры. Кроме определения стоит отметить несколько свойств этого выпуклого многоугольника.
Стороны параллелограмма, находящиеся напротив друг друга равны. Также равны друг другу и противоположные углы.
Пересечение отрезков, называемых диагоналями, образует угол в девяносто градусов. Если просуммировать квадраты их длин, то они составят сумму квадратов граней фигуры. Каждый такой отрезок образует два одинаковых треугольника и четыре равновеликих.
Любые два соседних угла при сложении дадут сто восемьдесят градусов.
При констатации факта, что геометрическая фигура обладает данными свойствами, можно утверждать, что она — параллелограмм. Таким образом, мы получим признаки этого четырехугольника, определяющие принадлежность фигуры именно к этому классу.
Площадь можно найти двумя способами. Первым будет являться поиск произведения синуса угла и длин, прилежащих к нему сторон. Второй способ — определение результата перемножения длин высоты и лежащей напротив нее грани.
Какой четырехугольник называется ромбом? Такой, у которого все из образовывающих его сторон равняются между собой. Эта геометрическая фигура обладает всеми свойствами и признаками параллелограмма. Еще одним свойством является факт, что в эту фигуру всегда вписывается окружность.
Параллелограмм, соседние стороны которого равны, однозначно определяется, как ромб. Площадь можно вычислить, как произведение квадрата стороны на синус одного из углов.
Видео:Прямоугольник. 8 класс.Скачать

Прямоугольник
Какой четырехугольник называется прямоугольником? Такой, который обладает углами в девяносто градусов. Так как он тоже является параллелограммом, на него распространяются свойства и признаки этого четырехугольника. Также о прямоугольнике можно сказать следующее:
- Диагонали этой фигуры имеют одинаковую длину.
- Площадь определяется путем умножения сторон друг на друга.
- В случае, когда угол параллелограмма составляет девяносто градусов – можно утверждать, что это прямоугольник.
Видео:Какой четырехугольник называется прямоугольником. Геометрия 8 класс. Глава 5Скачать

Квадрат
Следующий вопрос из тех, что мы рассмотрим в этой публикации, – какой четырехугольник называется квадратом? Это фигура, обладающая равными сторонами и углами в девяносто градусов. Исходя из указанных выше параметров, она обладает всеми теми же свойствами, которыми обладают прямоугольник и ромб. Соответственно имеет также их признаки.
К особенностям квадрата можно отнести уникальные свойства линий, соединяющих его противоположные вершины и называемых диагоналями. Они имеют одну длину и пересекаются под прямым углом.
Прикладное значение квадрата сложно переоценить. Благодаря своей универсальности, простоте определения площади и размеров, эта фигура широко используется в качестве эталонной меры. Число возведенное во вторую степень устойчиво называется математиками квадратом. С помощью квадратных единиц измеряют площадь, осуществляют интеграцию и общие приближения размеров на плоскости. Широко эта геометрическая концепция используется в архитектуре и ландшафтном дизайне.
Видео:Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Трапеция
Далее следует рассмотреть какой четырехугольник называется трапецией. Это будет фигура, имеющая расположенные параллельно друг другу стороны, называемые основаниями и непараллельные стороны, определяемые боковыми. Она образована четырьмя гранями и таким же количеством углов. Когда эти непараллельные отрезки равны, трапецию определяют как равнобокую. В случае, если у фигуры угол равен девяносто градусов, она будет считаться прямоугольной.
Такой четырехугольник, какой называется трапецией имеет еще один особый элемент. Линию, которая соединяет центры боковых сторон, называют средней. Длину ее можно определить, отыскав одну вторую результата сложения длин сторон, определяемых, как основания фигуры.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, длины диагонали и углы между боковыми сторонами и основаниям равны.
Вокруг такой трапеции всегда возможно описание окружности.
Вписывается окружность в такую фигуру, сумма длин боковых сторон которой одинакова с результатом сложения ее оснований.
Видео:Математика 2 класс (Урок№36 - Прямоугольник.)Скачать

Общие выводы по теме
В заключение можно сказать что в курсе геометрии достаточно доступно и подробно рассмотрен вопрос о том, какой четырехугольник называется квадратом. Несмотря на то, что в разных учебниках мы можем встретить некоторые отличия в последовательности изложения обозначенных выше тем, все они исчерпывающе освещают тему четырехугольников.
Видео:Четырёхугольник, прямоугольник, квадрат // Математика 1 классСкачать

Разница между квадратом и прямоугольником
Четырехугольником называют многоугольник, у которого четыре вершины и четыре стороны.
Иначе можно сказать, что четырёхугольником является геометрическая фигура в виде многоугольника, который имеет только четыре угла. Любой предмет или устройство, имеющее такую форму также можно назвать четырехугольником. Две стороны четырехугольника, которые по отношению друг к другу являются несмежными, называются противоположными. Два угла и две вершины, которые не являются соседними, называют противоположными.
Четырехугольник определяют, как параллелограмм, если у него противолежащие стороны попарно параллельны.
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Определение
Квадрат — это параллелограмм, у которого все четыре стороны равны и все четыре угла прямые.
Прямоугольник — это параллелограмм, у которого противолежащие стороны, которые параллельны друг другу, равны и все углы прямые.
Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Сравнение
Квадратом называют параллелограмм, у которого все четыре внутренних угла прямые. Все четыре стороны квадрата равны, то есть имеют одинаковую длину.
Прямоугольником называют параллелограмм, внутренние углы у которого прямые, и только противоположные стороны, которые параллельны друг другу, равны.
Для прямоугольника и квадрата характерны следующие свойства:
- все углы прямые;
- диагонали равны;
- в точке пересечения диагонали делятся пополам;
- противолежащие стороны параллельны друг другу и равны по длине.
Видео:Математика 29. Четырехугольники, прямоугольник, квадрат — Шишкина школаСкачать

Чем отличается прямоугольник от четырехугольника
Тема: Виды четырехугольников. Прямоугольник
- Обеспечить усвоение учащимися знаний о различных видах четырехугольников, прямоугольника.
- Развить умения классифицировать факты, делать выводы, строить прямоугольник и отличать его из ряда четырехугольников.
- Воспитание мотивов учения, положительного отношения к занятиям.
Тип урока – комбинированный.
Вид урока – дидактическая игра.
Методы и приемы обучения: диалогический и эвристический методы:
- организация труда в парах;
- фронтальная работа;
- оперативная форма проверки знаний (спецкарточки);
- демонстрация наглядных пособий;
- работа в бригадах.
- кодоскоп;
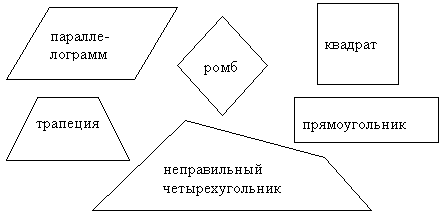
- плакат с видами четырехугольников;
- наглядные пособия к сказке;
- сигнальные карточки;
- перфокарты для каждого ученика с заготовленными таблицами;
- заготовки прямоугольников;
- ножницы, линейки, карандаши, чертежные треугольники;
- магнитная доска;
- прямоугольники с номерками;
- раздаточный материал (прямоугольники красного цвета для поощрения отвечающих);
- магнитофон.
Ход урока
Сегодня на уроке мы с вами совершим путешествие в удивительную страну Геометрию:
– Кто знает, что в переводе с греческого обозначает слово “геометрия”?
“Гео” – земля, “метрия” – измерение.
Наука эта появилась в Греции.
Сопровождать нас будет в нашем путешествии (учитель показывает сказочного героя) удивительный герой – волшебник.
– Всех вас он зашифровал, и вы будете путешествовать под зашифрованными номерами.
– Кто узнал его? (Старик Хоттабыч.)
– Кто написал книжку “Старик Хоттабыч”? (Лагин.)
Старик Хоттабыч очень старый волшебник и его знания устарели, поэтому он пришел к вам на урок и хочет узнать, что же сейчас изучают современные дети. Помогите волшебнику разобраться.
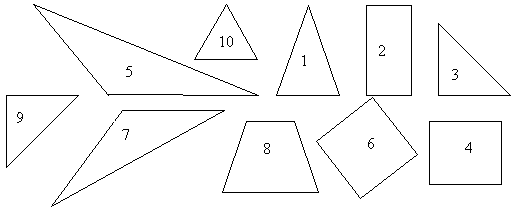
– Что изображено на доске? (Геометрические фигуры.)
– Определите на какие 2 группы вы могли бы разделить эти геометрические фигуры? (Треугольники и четырехугольники.)
Заполните карточку №1. Укажите номера треугольников и четырехугольников. Все дети указывают в карточке номера.
В это время 2 ученика фиксируют ответы на доске.
– Укажите во второй карточке номера треугольников по углам (тупоугольный, прямоугольный, остроугольный) и по сторонам (равносторонний и равнобедренный).
Работу выполняют по вариантам, а потом обмениваются карточками и осуществляют взаимопроверку в парах.
| Вариант №1: Карточка №2 | |
| Тупоугольный | |
| Вариант №1: Карточка №2 | |
| Равносторонний 1) Сегодня мы с нашим героем познакомимся с видами четырёхугольников, а именно; с прямоугольником, научимся его чертить и выделять среди других фигур Т.к. треугольников и четырёхугольников в геометрии много. Вот как выглядят некоторые из них: – Какие из них вы уже знаете? Дети называют те виды, которые знают. – Что общего у этих фигур, что их объединяет в одну группу? (4 стороны, 4 угла, 4 вершины.) – А чем один вид отличается от другого? (Длинами сторон и особенностями углов.) Учитель обращает внимание детей на таблицу и говорит определения. – фигура, у которой стороны не равны и не параллельны. 2) Помогите Хоттабычу из ряда четырехугольников найти похожие (1 3 5). – Как называются углы у фигур 1, 3, 5? (Прямые.) – А как бы вы назвали эти фигуры? (Прямоугольники.) – Попробуйте сказать, что же такое прямоугольник? Прямоугольник – геометрическая фигура, у которой все углы прямые и противоположные стороны равны. – Назовите вершины у прямоугольника АВСД? (А, В, С, Д – вершины.)
Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу. Видео:8 класс, 3 урок, ЧетырехугольникСкачать  Признаки и свойства прямоугольникаКак понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:
Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки. Формулы для вычисления длины сторонВ прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).
Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α — угол между диагональю и длиной, β — острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:
Периметр и площадь
Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:
Диагонали прямоугольникаВ задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:
Применяются следующие формулы для расчёта длины диагонали:
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать  Определение и свойства квадратаКвадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник. Четырёхугольник называют квадратом в следующих случаях:
К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:
Приведём часто используемые формулы для
Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать  Примеры вопросов и задачРазберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач. Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза? Решение: Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз. Вопрос 1. Четырёхугольник с прямыми углами — это квадрат? Решение: Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником. Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ. Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16. Вопрос 2. У прямоугольника все стороны равны или нет? Решение: Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком. Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.
Четырехугольником называют многоугольник, у которого четыре вершины и четыре стороны. Иначе можно сказать, что четырёхугольником является геометрическая фигура в виде многоугольника, который имеет только четыре угла. Любой предмет или устройство, имеющее такую форму также можно назвать четырехугольником. Две стороны четырехугольника, которые по отношению друг к другу являются несмежными, называются противоположными. Два угла и две вершины, которые не являются соседними, называют противоположными. Четырехугольник определяют, как параллелограмм, если у него противолежащие стороны попарно параллельны. Видео:8 класс, 7 урок, ПрямоугольникСкачать  ОпределениеКвадрат — это параллелограмм, у которого все четыре стороны равны и все четыре угла прямые. Прямоугольник — это параллелограмм, у которого противолежащие стороны, которые параллельны друг другу, равны и все углы прямые. Видео:Периметр прямоугольника. Как найти периметр прямоугольника?Скачать  СравнениеКвадратом называют параллелограмм, у которого все четыре внутренних угла прямые. Все четыре стороны квадрата равны, то есть имеют одинаковую длину. Прямоугольником называют параллелограмм, внутренние углы у которого прямые, и только противоположные стороны, которые параллельны друг другу, равны. Для прямоугольника и квадрата характерны следующие свойства: 🎥 Видео№400. Докажите, что если в четырехугольнике все углы прямые, то четырехугольник — прямоугольник.Скачать  ЧетырехугольникиСкачать  Математика 5 класс (Урок№29 - Четырёхугольники.)Скачать  | |



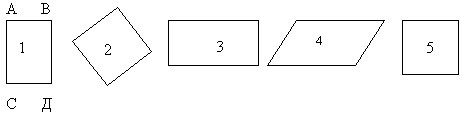
 В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.
В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.