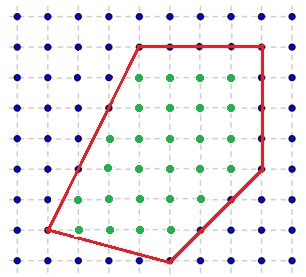
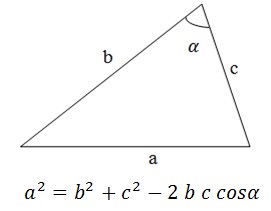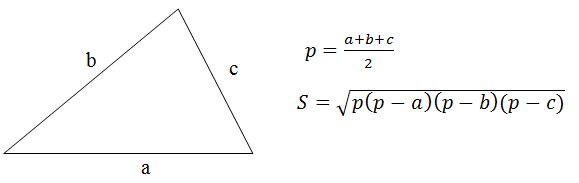- Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1
- Немного истории
- Вступление
- Немного теории о векторах
- А теперь займемся практикой
- Как эффективно определить, является ли многоугольник выпуклым, невыпуклым или сложным?
- 10 ответов
- Примечание: вычисление выпуклой оболочки набора точек совершенно необязательно, если вы просто хотите определить, представляет ли список точек, представляющих многоугольник, выпуклый многоугольник.
- 3.3 Определение выпуклости многоугольника
- Рекомендуемые файлы
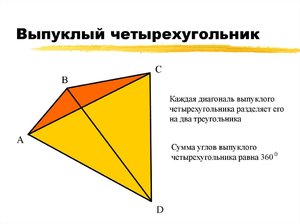
- Понятие выпуклого четырехугольника, его свойства и признаки
- Выпуклый четырехугольник
- Основные свойства и виды
- Является ли параллелограмм выпуклым четырехугольником?
- Свойство диагоналей выпуклого четырехугольника
- Другие свойства и признаки выпуклости четырехугольника
- 3.3 Определение выпуклости многоугольника
- Рекомендуемые файлы
- 🌟 Видео
Видео:№369. Найдите углы A, B и C выпуклого четырехугольника ABCD, еслиСкачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1
Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.
Немного истории
Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.
В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).
Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».
Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.
Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
Вступление
«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».
Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.
Немного теории о векторах
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.
Скалярное произведение векторов
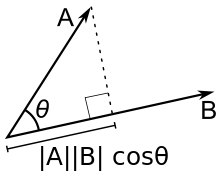
Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то скалярное произведение (a, b) = x1x2 + y1y2.
Косое произведение векторов
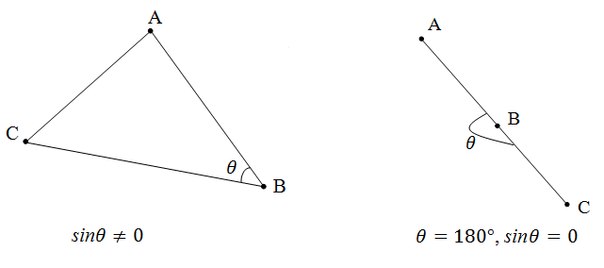
Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где 
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
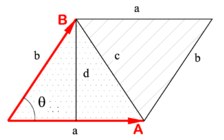
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.
А теперь займемся практикой
Начнем с треугольников
Задача №1
Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.
Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.
Задача №2
Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.
Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x1, y1), B(x2, y2) вычисляется по формуле √(x1-x2) 2 +(y1-y2) 2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.
Задача №3
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.
Решение
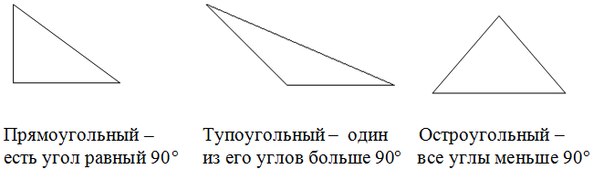
Вспомним, что представляют собой каждый вид треугольника.
Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
- Угол больше 90° – треугольник тупоугольный
- Угол меньше 90°– треугольник остроугольный
- Угол равен 90°– треугольник прямоугольный
Воспользуемся теоремой косинусов:
Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
- Если cosα > 0, то a 2 2 + c 2 – треугольник остроугольный
- Если cosα = 0, то a 2 = b 2 + c 2 – треугольник прямоугольный
- Если cosα 2 > b 2 + c 2 – треугольник тупоугольный
где a – большая сторона.
Задача №4
Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.
Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Задача №5
По данным сторонам треугольника найти его площадь.
Решение
Очевидно решение, заключается в применение формулы Герона.
Кстати, никого не интересовало доказательство этой формулы?
Задача №6
Вычислить площадь треугольника заданного координатами своих вершин.
Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x1, y1), b(x2, y2)
S = (x1y2 — x2y1) / 2 — ориентированная площадь треугольника
Задача №7
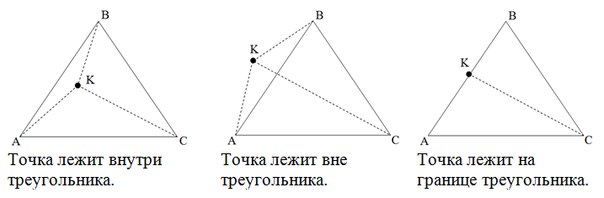
Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.
Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.
Метод площадей
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
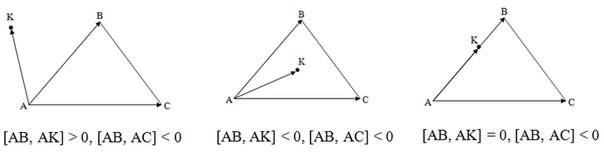
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.
В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача №8
Вычисление площади многоугольника заданного координатами своих вершин.
Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.
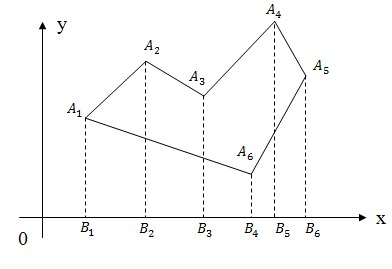
Метод трапеций
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = SA1 A2 B2 B1 + SA2 A3 B3 B2 + SA3 A4 B5 B3 + SA4 A5 B6 B5 + SA5 A6 B4 B6 + SA6 A1 B1 B4
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
SA1 A2 B2 B1 = 0.5 * (A1B1 + A2B2) *(B2 — B1)
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
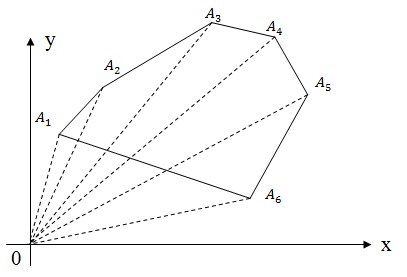
Метод треугольников
Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть.
Задача №9
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.
Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача №10
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Решение
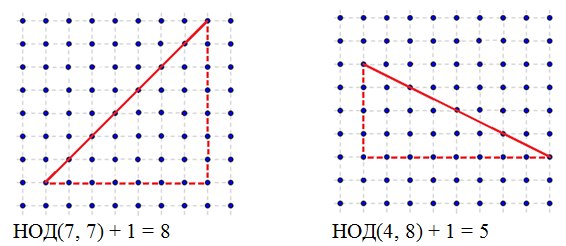
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.
Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример:
S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!
Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Как эффективно определить, является ли многоугольник выпуклым, невыпуклым или сложным?
из man-страницы для XFillPolygon :
если shape is комплекс путь может иметь самопересечений. Обратите внимание, что смежные совпадающие точки На пути не рассматриваются как самосечение.
если shape is выпуклой, для каждой пары точек внутри многоугольника, отрезок прямой, соединяющий их, не пересекает путь. Если известно клиенту, указав выпуклой может улучшить производительность. Если указать выпуклой для пути, который не является выпуклым, Результаты Графики не определены.
если shape is Nonconvex, путь не пересекается сам с собой, но форма не является полностью выпуклой. Если известно клиенту, указав Nonconvex вместо комплекс может повысить производительность. Если указать Nonconvex для a self-intersecting path, Результаты Графики не определены.
у меня проблемы с производительностью с fill XFillPolygon и, как следует из справочной страницы, первый шаг, который я хочу сделать, — указать правильную форму многоугольника. В настоящее время я использую комплекс на всякий случай.
существует ли эффективный алгоритм для определения того, является ли многоугольник (определенный серией координат) выпуклым, невыпуклым или сложным?
Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

10 ответов
Примечание: вычисление выпуклой оболочки набора точек совершенно необязательно, если вы просто хотите определить, представляет ли список точек, представляющих многоугольник, выпуклый многоугольник.
предполагая, что все ваши полигоны находятся в порядке против часовой стрелки, в тот момент, когда ваш не начальный полярный угол делает левый поворот, вы знаете, что он не выпуклый.
вы могли бы увидеть, если сегменты линии пересекайтесь друг с другом, чтобы выяснить, является ли многоугольник сложным (но я не уверен, что это самый быстрый способ).
вы можете сделать вещи намного проще, чем алгоритм подарочной упаковки. это хороший ответ, когда у вас есть набор точек без какой-либо конкретной границы, и нужно найти выпуклую оболочку.
напротив, рассмотрим случай, когда многоугольник не является самопересекающимся и состоит из набора точек в списке, где последовательные точки образуют границу. В этом случае гораздо проще выяснить, является ли многоугольник выпуклым или нет (и вам не нужно вычислять какие-либо углы, либо):
для каждой последовательной пары ребер многоугольника (каждого триплета точек) вычислите z-компонент поперечного произведения векторов, определенных ребрами, указывающими на точки в порядке возрастания. Взять векторное произведение этих векторов:
многоугольник выпукл, если z-компоненты поперечных произведений либо все положительные, либо все отрицательные. В противном случае многоугольник называется невыпуклым.
Если есть N точек, убедитесь, что вы вычисляете N перекрестных произведений, например, обязательно используйте триплеты (p[N-2],p[N-1],p[0]) и (p[N-1],p[0],p[1]).
если многоугольник является самопересекающимся, то это не соответствует техническому определению выпуклости даже если его направленные углы находятся в одном направлении, в этом случае вышеуказанный подход не даст правильного результата.
следующая функция/метод Java является реализацией алгоритма, описанного в ответ.
алгоритм гарантированно работает до тех пор, пока вершины упорядочены (по часовой стрелке или против часовой стрелки), и у вас нет самопересекающихся ребер (т. е. он работает только для простые многоугольники).
этот вопрос теперь является первым элементом в Bing или Google при поиске «определить выпуклый многоугольник.- Однако ни один из ответов недостаточно хорош.
The принятый ответ от @EugeneYokota работает, проверяя, можно ли сделать неупорядоченный набор точек выпуклым многоугольником, но это не то, что просил OP. Он попросил способ проверить, является ли данный многоугольник выпуклым или нет. («Многоугольник» в информатике обычно определено [как в документация XFillPolygon] как упорядоченный массив 2D точек, с последовательными точками, Соединенными со стороной, а также последней точкой к первой.) Кроме того, алгоритм подарочной упаковки в этом случае будет иметь временную сложность O(n^2) на n points-что намного больше, чем необходимо для решения этой проблемы, в то время как вопрос требует эффективного алгоритма.
ответ @ JasonS вместе с другие ответы, которые следуют его идее, принимает звездчатых многоугольников например,пентаграмма или в комментарии @zenna, но звездные полигоны не считаются выпуклыми. Как @plasmacel отмечает в комментарии, это хороший подход для использования, если у вас есть предварительные знания о том, что многоугольник не является самопересекающимся, но он может потерпеть неудачу, если у вас нет этих знаний.
@Sekhat это!—10—> — это правильно, но он также имеет время-сложность O(n^2) и, таким образом, является неэффективным.
@ LorenPechtel добавил ответ после ее редактирования лучше всего здесь, но это неопределенно.
правильный алгоритм с оптимальной сложностью
алгоритм, который я здесь представляю, имеет временную сложность O(n) , правильно проверяет, является ли многоугольник выпуклым или нет, и проходит все тесты, которые я бросил на него. Идея заключается в Траверс сторон многоугольника, отмечая направление каждой стороны и подписанное изменение направления между последовательными сторонами. «Подписано» здесь означает, что левый-положительный, а правый-отрицательный (или наоборот), а прямой-ноль. Эти углы нормируются, чтобы быть между минус-pi (эксклюзив) и pi (включительно). резюме все эти углы изменения направления (a.к. a прогиб углы) вместе приведет к плюс-или-минус один ход (т. е. 360 Градусы) для выпуклого многоугольника, в то время как звездообразный многоугольник (или самопересекающаяся петля) будет иметь другую сумму ( n * 360 градусов, для n повороты в целом, для полигонов, где все углы отклонения имеют один и тот же знак). Поэтому мы должны проверить, что сумма углов изменения направления равна плюс-минус одному повороту. Мы также проверяем, что углы изменения направления все положительные или все отрицательные и не обратные (радианы pi), все точки являются фактическими 2D точками, и что последовательные вершины не идентичны. (Этот последний момент спорен-вы можете разрешить повторные вершины,но я предпочитаю запретить их.) Комбинация этих проверок захватывает все выпуклые и невыпуклые многоугольники.
вот код для Python 3, который реализует алгоритм и включает в себя некоторые незначительные эффективности. Код выглядит длиннее, чем на самом деле, из-за строк комментариев и бухгалтерии, участвующих во избежание повторных точечных обращений.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

3.3 Определение выпуклости многоугольника
Определение выпуклости многоугольника.
Алгоритм Кируса–Бэка предполагает наличие выпуклого многоугольника, используемого в качестве окна.
Однако на практике весьма часто возникает задача отсечения многоугольником, а информация о том, является он выпуклым или нет изначально не задается. В таком случае, прежде чем начать процедуру отсечения необходимо определить какой задан многоугольник – выпуклый или нет.
Дадим некотрые определения выпуклости многоугольника
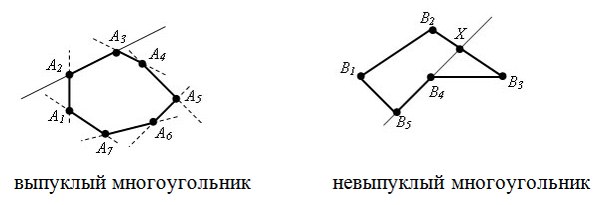
Выпуклым считается многоугольник, для которого выполняется одно из ниже перечисленных условий:
1) в выпуклом многоугольнике все вершины располагаются по одну сторону от линии, несущей любое ребро (по внутреннюю сторону относительно данного ребра);
2) все внутренние углы многоугольника меньше 180 о ;
3) все диагонали, связывающие вершины многоугольника, лежат внутри этого многоугольника;
Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Рекомендуемые файлы
4) все углы многоугольника обходятся в одном направлении (Рис. 3.3‑1).
Для выработки аналитического представление последнего критерия выпуклости, используем векторное произведение.
Векторное произведение W двух векторов a и b (Рис. 3.3‑2 а) определяется как:
 |
— ax , ay , az и bx , by , bz являются проекциями на оси координат X , Y , Z , соответственно, векторов – сомножителей a и b ,
— i , j , k – единичные векторы по координатным осям X , Y , Z .
 |
Если рассматривать двумерное представление многоугольника как представление его в координатной плоскости XY трехмерной системе координат X , Y , Z (Рис. 3.3‑2 b ), то выражение для формирования векторного произведения векторов U и V , где векторы U и V являются соседними ребрами, образующими угол многоугольника, можно записать в виде определитель:
Вектор векторного произведения перпендикулярен плоскости, в которой находятся вектора-сомножители. Направление вектора произведения определяется по правилу буравчика или по правилу винта с правой нарезкой.
Для случая, представленного на Рис. 3.3‑2 b ), вектор W , соответствующий векторному произведению векторов V , U , будет иметь ту же направленность, что и направленность координатной оси Z .
Учитывая то, что проекции на ось Z векторов –сомножителей в этом случае равны нулю, векторное произведение можно представить в виде:

Единичный вектор k всегда положительный, следовательно, знак вектора w векторного произведения будет определяться только знаком определителя D в выше приведенном выражении. Отметим, что на основании свойства векторного произведения, при перестановке местами векторов-сомножителей U и V знак вектора w будет меняться на противоположный.
Отсюда следует, что, если в качестве векторов V и U рассматривать два соседних ребра многоугольника, то порядок перечисления векторов в векторном произведении можно поставить в соответствие c обходом рассматриваемого угла многоугольника или ребер, образующих этот угол. Это позволяет использовать в качестве критерия определения выпуклости многоугольника правило:
если для всех пар ребер многоугольника выполняется условие:
 |
Если знаки векторных произведений для отдельных углов не совпадают, то многоугольник не выпуклый.
Так как ребра многоугольник задаются в виде координат их концевых точек, то для определения знака векторного произведения удобнее использовать определитель:
Если Вам понравилась эта лекция, то понравится и эта — 4 — Искусство.
Легко показать, что этот определитель эквивалентен определителю в выражении (3.3-1).
Видео:Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Понятие выпуклого четырехугольника, его свойства и признаки
Выпуклый четырехугольник — это фигура, состоящая из четырех сторон, соединенных между собой в вершинах, образующих вместе со сторонами четыре угла, при этом сам четырехугольник всегда находится в одной плоскости относительно прямой, на которой лежит одна из его сторон. Другими словами, вся фигура находится по одну сторону от любой из ее сторон.
Как видно, определение довольно легко запоминающееся.
Видео:№429. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащихСкачать

Выпуклый четырехугольник
Основные свойства и виды
К выпуклым четырехугольникам можно отнести практически все известные нам фигуры, состоящие из четырех углов и сторон. Можно выделить следующие:
Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.
Все эти фигуры объединяет не только то, что они четырехугольные, но и то, что они еще и выпуклые. Достаточно просто рассмотреть схему:
На рисунке изображена выпуклая трапеция. Тут видно, что трапеция находится на одной плоскости или по одну сторону от отрезка [AB]. Если провести аналогичные действия, можно выяснить, что и в случае со всеми остальными сторонами трапеция является выпуклой.
Является ли параллелограмм выпуклым четырехугольником?
Теперь, представьте себе квадрат или прямоугольник. По своим основным свойствам они являются еще и параллелограммами, то есть все их стороны расположены попарно параллельно. Только в случае с прямоугольником длина сторон может быть разной, а углы прямые (равные 90 градусам), квадрат — это прямоугольник, у которого все стороны равны и углы также прямые, а у параллелограмма длины сторон и углы могут быть разными.
В итоге, сумма всех четырех углов четырехугольника должна быть равна 360 градусам. Легче всего это определить по прямоугольнику: все четыре угла прямоугольника прямые, то есть равны 90 градусам. Сумма этих 90-градусных углов дает 360 градусов, другими словами, если сложить 90 градусов 4 раза, получится необходимый результат.
Свойство диагоналей выпуклого четырехугольника
Диагонали выпуклого четырехугольника пересекаются. Действительно, это явление можно наблюдать визуально, достаточно взглянуть на рисунок:
На рисунке слева изображен невыпуклый четырехугольник или четырехсторонник. Как угодно. Как видно, диагонали не пересекаются, по крайней мере, не все. Справа изображен выпуклый четырехугольник. Тут уже наблюдается свойство диагоналей пересекаться. Это же свойство можно считать признаком выпуклости четырехугольника.
Другие свойства и признаки выпуклости четырехугольника
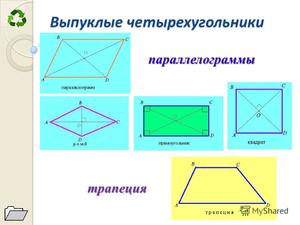
Итак, известны основные признаки и свойства:
- сумма углов четырехугольника равна 360 градусам;
- диагонали фигур пересекаются в одной точке.
Далее рассмотрим каждый четырехугольник по отдельности.
Прямоугольник. Эта фигура имеет все те же свойства и признаки, что и параллелограмм, но при этом все углы его равны 90 градусам. Отсюда и название — прямоугольник.
Квадрат, тот же параллелограмм, но углы его прямые как у прямоугольника. Из-за этого квадрат в редких случаях называют прямоугольником. Но главным отличительным признаком квадрата помимо уже перечисленных выше, является то, что все четыре его стороны равны.
Трапеция — очень интересная фигура. Это тоже четырехугольник и тоже выпуклый. В этой статье трапеция уже рассматривалась на примере рисунка. Понятно, что она тоже выпуклая. Главным отличием, а соответственно признаком трапеции является то, что ее стороны могут быть абсолютно не равны друг другу по длине, а также ее углы по значению. При этом фигура всегда остается на одной плоскости относительно любой из прямых, которая соединяет любые две ее вершины по образующим фигуру отрезкам.
Ромб — не менее интересная фигура. Отчасти ромбом можно считать квадрат. Признаком ромба является тот факт, что его диагонали не только пересекаются, но и делят углы ромба пополам, а сами диагонали пересекаются под прямым углом, то есть, они перпендикулярны. В случае, если длины сторон ромба равны, то диагонали тоже делятся пополам при пересечении.
Дельтоиды или выпуклые ромбоиды (ромбы) могут иметь разную длину сторон. Но при этом все равно сохраняются как основные свойства и признаки самого ромба, так и признаки и свойства выпуклости. То есть, мы можем наблюдать, что диагонали делят углы пополам и пересекаются под прямым углом.
Сегодняшней задачей было рассмотреть и понять, что такое выпуклые четырехугольники, какие они бывают и их основные признаки и свойства. Внимание! Стоит напомнить еще раз, что сумма углов выпуклого четырехугольника равна 360 градусам. Периметр фигур, например, равен сумме длин всех образующих фигуру отрезков. Формулы расчета периметра и площади четырехугольников будут рассмотрены в следующих статьях.
Видео:Скалярное произведение векторов. 9 класс.Скачать

3.3 Определение выпуклости многоугольника
Определение выпуклости многоугольника.
Алгоритм Кируса–Бэка предполагает наличие выпуклого многоугольника, используемого в качестве окна.
Однако на практике весьма часто возникает задача отсечения многоугольником, а информация о том, является он выпуклым или нет изначально не задается. В таком случае, прежде чем начать процедуру отсечения необходимо определить какой задан многоугольник – выпуклый или нет.
Дадим некотрые определения выпуклости многоугольника
Выпуклым считается многоугольник, для которого выполняется одно из ниже перечисленных условий:
1) в выпуклом многоугольнике все вершины располагаются по одну сторону от линии, несущей любое ребро (по внутреннюю сторону относительно данного ребра);
2) все внутренние углы многоугольника меньше 180 о ;
3) все диагонали, связывающие вершины многоугольника, лежат внутри этого многоугольника;
4) все углы многоугольника обходятся в одном направлении (Рис. 3.3‑1).
Видео:№370. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1, 2, 4, 5.Скачать

Рекомендуемые файлы
Для выработки аналитического представление последнего критерия выпуклости, используем векторное произведение.
Векторное произведение W двух векторов a и b (Рис. 3.3‑2 а) определяется как:
 |
— ax,ay,az и bx,by,bz являются проекциями на оси координат X,Y,Z, соответственно, векторов – сомножителей a и b,
— i, j, k – единичные векторы по координатным осям X, Y, Z.
 |
Если рассматривать двумерное представление многоугольника как представление его в координатной плоскости XY трехмерной системе координат X,Y,Z (Рис. 3.3‑2 b), то выражение для формирования векторного произведения векторов U и V , где векторы U и V являются соседними ребрами, образующими угол многоугольника, можно записать в виде определитель:
Вектор векторного произведения перпендикулярен плоскости, в которой находятся вектора-сомножители. Направление вектора произведения определяется по правилу буравчика или по правилу винта с правой нарезкой.
Для случая, представленного на Рис. 3.3‑2 b), вектор W, соответствующий векторному произведению векторов V,U, будет иметь ту же направленность, что и направленность координатной оси Z.
Учитывая то, что проекции на ось Z векторов –сомножителей в этом случае равны нулю, векторное произведение можно представить в виде:

Единичный вектор k всегда положительный, следовательно, знак вектора w векторного произведения будет определяться только знаком определителя D в выше приведенном выражении. Отметим, что на основании свойства векторного произведения, при перестановке местами векторов-сомножителей U и V знак вектора w будет меняться на противоположный.
Отсюда следует, что, если в качестве векторов V и U рассматривать два соседних ребра многоугольника, то порядок перечисления векторов в векторном произведении можно поставить в соответствие c обходом рассматриваемого угла многоугольника или ребер, образующих этот угол. Это позволяет использовать в качестве критерия определения выпуклости многоугольника правило:
Если Вам понравилась эта лекция, то понравится и эта — 4 — Искусство.
если для всех пар ребер многоугольника выполняется условие:
 |
Если знаки векторных произведений для отдельных углов не совпадают, то многоугольник не выпуклый.
Так как ребра многоугольник задаются в виде координат их концевых точек, то для определения знака векторного произведения удобнее использовать определитель:
Легко показать, что этот определитель эквивалентен определителю в выражении (3.3-1).
🌟 Видео
Математический анализ, 14 урок, Выпуклость и вогнутость функцииСкачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

23. Выпуклые четырехугольникиСкачать

№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

#58. Олимпиадная задача о четырехугольникеСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

ОГЭ Задание 24 Площадь выпуклого четырехугольника с перпендикулярными диагоналямиСкачать

Как выпуклый четырёхугольник разрезать по прямой, содержащей его вершину, на две равновеликие части?Скачать

Угол между векторами. 9 класс.Скачать

Сумма углов в выпуклом многоугольнике. Выпуклый четырехугольник.Скачать