Уравнение касательной к окружности проходящей через точку на окружности (5 видео)

Определение формулы касательной к окружности

Коэффициенты окружности

Точка на окружности, через которую надо провести касательную

Общая формула окружности

Уравнение касательной в указанной точке

Содержание

Касательная к окружности
Примеры
Касательная к окружности
Свойство касательной
Теорема, обратная теореме о свойстве касательной
Построение касательной к окружности
Касательная к окружности — свойства, теорема и уравнение
Общие сведения
Построение касательных
Основные свойства
Частные случаи
Доказательства утверждений
🔍 Видео

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Касательная к окружности

Если не использовать понятие производной, и взять объяснение из учебников середины прошлого века, то «Касательная к окружности — это прямая пересекающая окружность в двух совпадающих точках»

Окружность на плоскости может быть представлена в виде нескольких исходных данных

1. В виде координат центра окружности (x0,y0) и её радиуса R.

2. В виде общего уравнения

В виде параметрического вида и в полярных координатах мы рассматривать не будем, так как там формулы тоже на базируются на координатах центра окружности и радиусе.

Наша задача, зная параметры окружности и точку принадлежащую этой окружности вычислить параметры касательной к этой окружности.

Эта задача, является частным решением более общего калькулятор касательная к кривой второго порядка

Итак, если окружность выражена формулой

Уравнение касательной к окружности если нам известны параметры общего уравнения таково:

Таким образом, зная все коэффициенты, мы очень легко найдем уравнение касательной в заданной точке.

ВАЖНО: При указании точки, она должна быть обязательно(!!) принадлежать окружности,
и не быть точкой в какой либо стороне. В противном случае, уравнение касательной будет неверным.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Примеры

Вычислить уравнение касательной в точке (13.8, 0) к окружности выраженной формулой

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательная к окружности

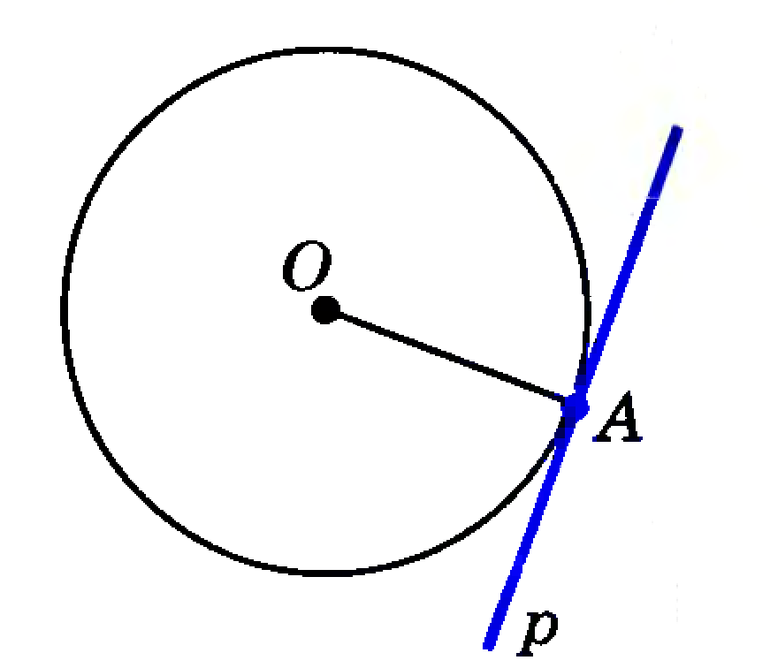
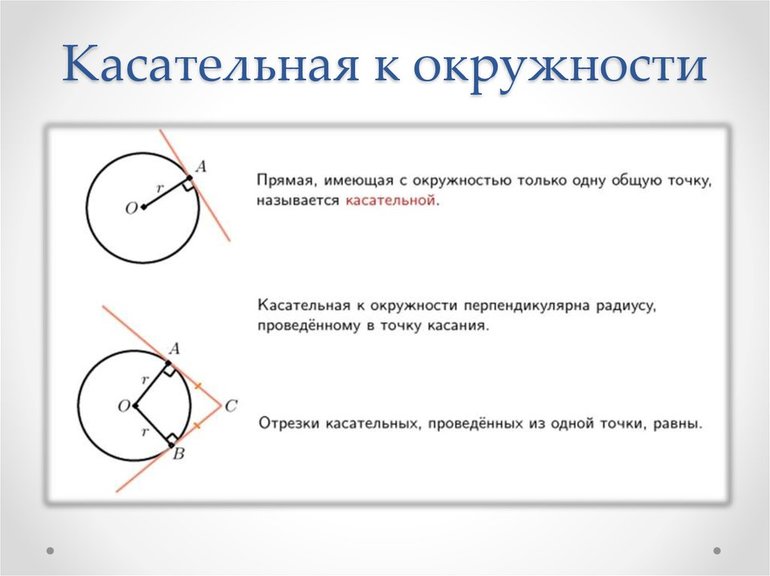
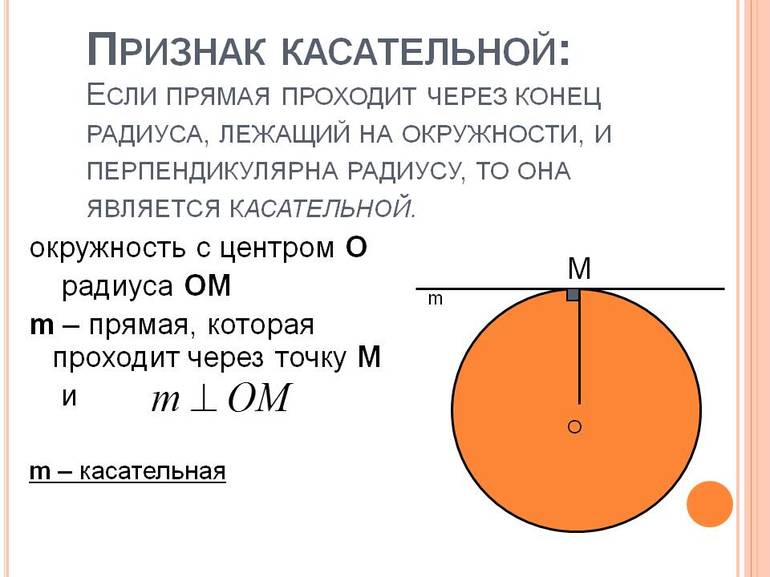
Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.

Уравнение касательной к окружности проходящей через точку на окружности

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Свойство касательной

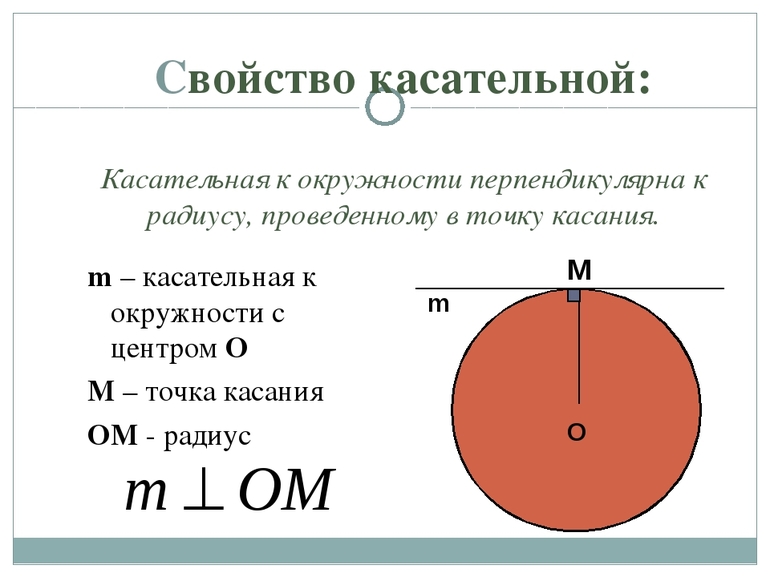
Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.

Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)

Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.

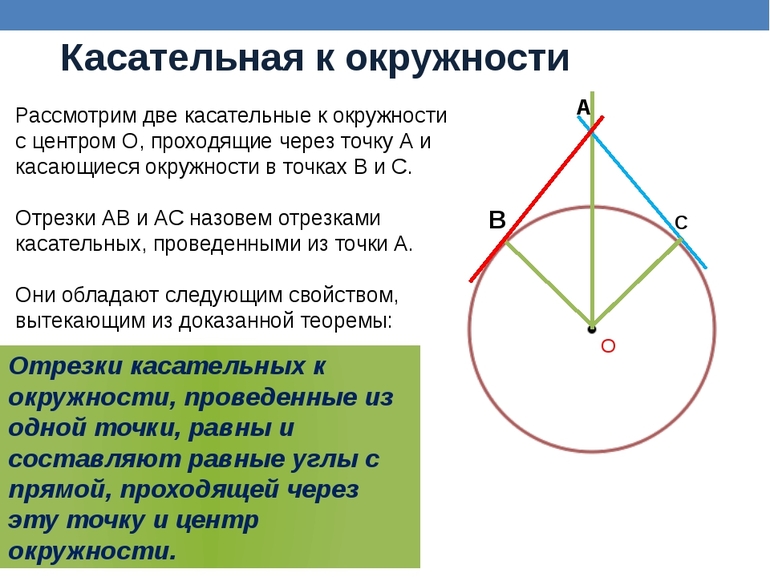
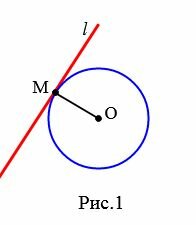
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.

Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.

Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Теорема, обратная теореме о свойстве касательной

Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.

Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).

Видео:Построение касательной к окружности.Скачать

Построение касательной к окружности

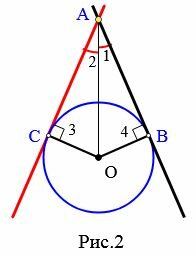
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).

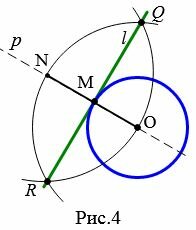Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.

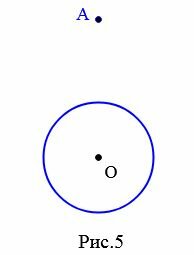
Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).

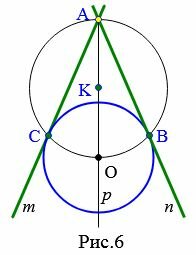Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.

Видео:Уравнение окружности (1)Скачать

Касательная к окружности — свойства, теорема и уравнение

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Общие сведения

Важно знать терминологию, соотношения и теоремы для решения задач этого класса. Касательной к окружности называется прямая, которая имеет с ней только одну точку соприкосновения. Прямая — это линия, не имеющая границ, т. е. она ничем не ограничена. Окружностью называется геометрическое место точек, удаленных от центра на одинаковые расстояния.

Следует отметить, что касательные бывают внешними и внутренними. Внешней называет прямая линия, проходящая с внешней стороны окружности. Внутренние касательные пересекают отрезок, который соединяет центры двух окружностей. Последний тип прямых не существует, когда два круга пересекаются. Касательные нужно уметь правильно строить, поскольку от этого зависит правильность решения задачи.

Построение касательных

Для построения касательной к окружности следует на последней отметить произвольную точку. Затем необходимо через нее провести прямую. Нужно отметить, что у круга может быть несколько таких прямых. Когда даны две окружности, тогда можно проводить не только внешние, но и внутренние. Существует определенный алгоритм, по которому можно построить первый тип:

Начертить 2 окружности с центрами в точках О1 и О2. При этом должно соблюдаться условие r1 > r2, где r1 и r2 — радиусы I и II соответственно.
Нарисовать III окружность с центром в О1 и радиусом r3 = r1 — r2.
Провести 2 касательные из точки О2 к III. Они параллельны искомым, поскольку радиусы I и II уменьшаются на r2.

Существует более простая модель построения таких прямых. Для этого следует начертить один круг, а затем отметить две произвольные точки на его противоположных сторонах. Далее начертить II круг, превышающий I по радиусу. Отметить на нем точки, воспользовавшись подобием, т. е. они должны быть в тех же местах, что и на I. Затем провести прямые, которые должны соприкасаться с I и II кругами только в одной точке.

Для построения внутренних касательных существует определенная методика. В интернете можно найти много информации. В одних источниках алгоритм построения является сложным, а в других — простым. Однако есть один метод, позволяющий осуществить данную операцию. Специалисты описали его на «понятном» языке для новичков. Суть методики заключается в следующем:

Необходимо построить два круга, которые не пересекаются, с радиусами r1 и r2. Расстояния между ними должно составлять r1 + r2.
Соединить их центры (середины) отрезком.
Отметить на нем среднюю точку, которая делит его на две равные части.
Через точку, полученную на третьем шаге методики, провести прямую. Она должна иметь только одну точку соприкосновения с I и II окружностями.
Аналогично провести еще одну прямую.
Искомые прямые являются внутренними касательными.

Далее нужно рассмотреть некоторые свойства, на основании которых можно решать задачи и доказывать геометрические тождества.

Основные свойства

Свойства — утверждения, полученные в результате доказательства теорем о касательной к окружности. Первые нет необходимости доказывать, поскольку об этом уже позаботились математики. Они выделяют всего 4 свойства касательных к окружности:

Если провести из одной точки две касательные к некоторой окружности, то отрезки, лежащие на них, будут равны. Искомый угол будет делиться радиусом пополам.
Любая касательная и радиус, проведенный к ее точке, образуют прямой угол. Справедливо и обратное утверждение: радиус, который проведен в точку касания, перпендикулярен данной прямой.
Вся секущая, умноженная на свою внешнюю часть, равна квадрату расстояния касательной, которая проведена из общей с ней точки.
Образованный угол между касательной и секущей, эквивалентен градусной мере угла, который опирается на образованную хорду.

Для рассмотрения I свойства необходимо начертить окружность с центром О1. Затем нужно отметить точку М вне окружности. Из М провести одну прямую, которая соприкасается с кругом в точке А. Такую же операцию следует проделать и для другой касательной. Точку соприкосновения назвать В. Отрезки АМ и ВМ равны между собой.

Если провести радиусы к точкам А и В, то можно сделать вывод, что углы являются прямыми. Чтобы понять третье свойство, необходимо начертить окружность и отметить некоторую точку М за ее пределами. После этого следует из искомой точки провести секущую и касательную. Первой называется прямая, проходящая через окружность и пересекающая ее в двух точках. Для касательной точку соприкосновения необходимо обозначить А. Тогда секущая пересекает круг в точках В (ближняя) и С (дальняя). В результате этого получается такое соотношение: АМ 2 = АВ * МС.

Когда для произвольной окружности существуют касательная и секущая, тогда между ними образуется некоторый угол.

Хорда, полученная в результате прохождения через окружность, образует также угол. Он опирается на искомую хорду и является вписанным. Следовательно, по свойству градусные меры углов равны между собой. Далее нужно разобрать частные случаи, на основании которых можно сделать вывод о количестве касательных.

Когда окружность вписана в ромб, тогда их точки касания нужно рассматривать по первому свойству. Радиус окружности можно найти по следующим формулам:

Через диагонали (d1, d2) и сторону (a): r = (d1 * d2) / 4а.
Только по диагоналям: r = (d1 * d2) / [(d1)^2 + (d2)^2]^(½).

Следует отметить, что у ромба две диагонали. Они различаются по размеру. Одна из них больше другой (d1 > d2).

Частные случаи

В некоторых задачах нужно определить количество касательных у двух окружностей. Можно выполнить ряд сложных и трудоемких доказательств. В результате этого будет потрачено много времени, а можно воспользоваться уже готовыми дополнительными свойствами:

Четыре касательных: круги не соприкасаются, т. е. d > r1 + r2 (значение диаметра больше суммы радиусов r1 и r2).
Две общие внешние и одна внутренняя: окружности соприкасаются только в одной точке (d = r1 + r2).
Только две внешние: пересечение окружностей в двух точках (|r1 — r2| d > — r1 — r2).
Внутренняя общая (одна): соприкасаются внутри (d = |r2 — r1|).
Четыре: при d > |r1 — r2|.

Когда заданы окружности, радиус одной из которых равен 0, тогда «нулевой» круг эквивалентен двойной точке. Прямая является двойной и проходит через эту точку. В этом случае математики определяют всего две внешних. Если r1 = r2 = 0, то всего 4 внешних общих касательных. Далее для решения задач нужно разобрать доказательства некоторых свойств.

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Доказательства утверждений

Очень важно знать доказательства некоторых свойств и теорем, поскольку одним из типов задач считаются упражнения повышенной сложности, требующие логических расчетов в общем виде. Например, нужно доказать, что касательная образует с радиусом, проведенным к точке касания, прямой угол. Существует тип доказательства от противного.

Для этого следует предположить, что искомый угол не равен 90 градусам. Пусть дана некоторая касательная р. Она имеет с кругом общую точку А. Нужно провести к ней перпендикуляр (радиус). Далее нужно провести из центра О отрезок ОВ на р. Образуется прямоугольный треугольник АВО с гипотенузой ОВ. Если опираться на утверждение от противного, то гипотенуза будет меньше катета (d 2 + y 2 = 2x + 6y + 19), проходящих через координаты х =0 у= -14. Для решения задачи следует действовать по такому алгоритму:

Перенести все слагаемые, кроме 19, в левую сторону: х 2 + y 2 — 2x — 6y = 19.
Выделить полный квадрат для окончательной записи уравнения окружности: х 2 — 2x + 1 — 1 + y 2 — 6y +9 — 9 = (х — 1)^2 + (y — 3)^2 = 29.
Уравнение прямой, проходящей через (0;-14) в общем виде: y — (-14) = k * (x — 0) или у = кх — 14.
Составить систему уравнений: (х — 1)^2 + (y — 3)^2 = 29 и у = кх — 14.
Подставить второе в первое: (х — 1)^2 + (кх — 14 — 3)^2 = 29.
Упростить выражение: (х — 1)^2 + (кх — 14 — 3)^2 — 29 = х 2 — 2x + 1 +k 2 * x 2 — 34kx + 289 — 29 = (1 + k 2 ) * x 2 — 2 * (17k + 1) + 261.
Решением уравнения должен быть один корень: D/4 = 0.
Упростить тождество: D/4 = (-(17k + 1))^2 — 261 (1 + k 2 ) = 289k 2 + 34k + 1 — 261 — 261k 2 = 28k 2 + 34k — 260 = 0.
Найти значение D: 17 2 — 28 * (-260) = 289 + 7280 = 7569.
Первый коэффициент к1 = (-17 — 87) / 28 = -26/7.
Коэффициент к2 = (-17 + 87) / 28 = 5/2.
Записать уравнения прямых с учетом к1 и к2: у1 = (-26/7) * х — 14 (26х + 7у + 98 = 0) и у2 = (5/2) * х — 14 (5х — 2у — 28 = 0).

Следует отметить, что уравнение окружности с радиусом, равным единице, описывается функцией x 2 + y 2 = 1. Эта запись применяется для решения задач в общем виде. Прямая — функция, описанная прямой пропорциональностью у = кх + b. Чтобы связать окружность и касательные, нужно составить систему уравнений. Этот математический ход объясняется тем, что у функций должны быть общие решения (точка на окружности). После решения можно выполнить проверочные вычисления, подставив корни в систему.