Внутренние накрест лежащие углы при параллельных прямых равны (2 видео)

Внутренние накрест лежащие углы

Внутренние накрест лежащие углы — один из видов углов, образованных при пересечении двух прямых секущей.

Две прямые разбивают плоскость на внутреннюю (внутри между прямыми) и внешнюю области. Углы, лежащие во внутренней части, так и называются — внутренние.

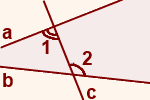
Внутренние накрест лежащие углы — это углы, которые лежат во внутренней области по разные стороны от секущей (накрест друг от друга).

При пересечении двух прямых секущей образуется две пары внутренних накрест лежащих углов.

∠1 и∠2 — внутренние накрест лежащие углы при прямых a и b и секущей c.

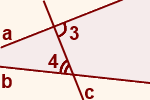
∠3 и∠4 — внутренние накрест лежащие углы при прямых a и b и секущей c.

Из всех внутренних накрест лежащих углов наибольший интерес представляют углы при параллельных прямых.

Свойство параллельных прямых

Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.

Если a ∥ b, то

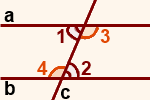
∠1 = ∠2

∠3 = ∠4

(как внутренние накрест лежащие углы при a ∥ b и секущей c).

Признак параллельных прямых

Если внутренние накрест лежащие углы равны, то прямые параллельны.

∠1=∠2.

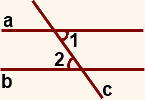
А так как эти углы — внутренние накрест лежащие при прямых a и b и секущей c,

то a ∥ b (по признаку параллельных прямых).

Равенство внутренних накрест лежащих углов при параллельных прямых используется, в частности, при доказательстве равенства треугольников и подобия треугольников.

Содержание

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Признаки параллельности прямых
Углы, образующиеся при пересечении двух прямых третьей прямой
Признаки параллельности двух прямых
📺 Видео

Видео:ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Видео:Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Признаки параллельности прямых

При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Углы, образующиеся при пересечении двух прямых третьей прямой

Рисунок	Определение углов
	Внутренние накрест лежащие углы
	Внутренние накрест лежащие углы
	Внешние накрест лежащие углы
	Внешние накрест лежащие углы
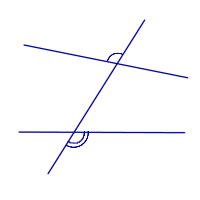	Соответственные углы



	Внутренние односторонние углы
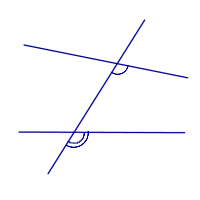	Внутренние односторонние углы
	Внешние односторонние углы
	Внешние односторонние углы

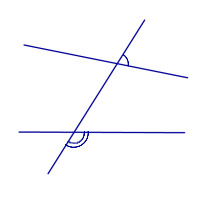Внутренние накрест лежащие углы

Внешние накрест лежащие углы

Соответственные углы

Внутренние односторонние углы

Внешние односторонние углы

Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.

Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Признаки параллельности двух прямых

Рисунок	Признак параллельности
	Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны

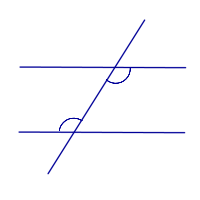	Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны

	Прямые параллельны тогда и только тогда, когда соответственные углы равны



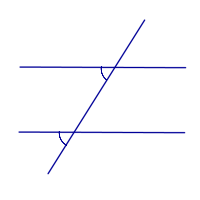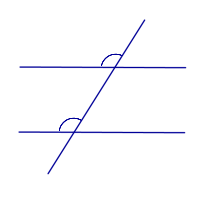	Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

	Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда соответственные углы равны

Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Рисунок	Признак параллельности
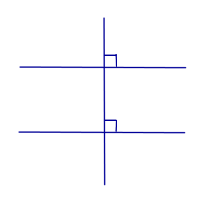	Две прямые, перпендикулярные к третьей прямой, параллельны

Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых

Рисунок	Признак параллельности
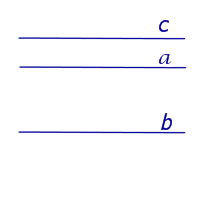	Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c

Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c

Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.

Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.