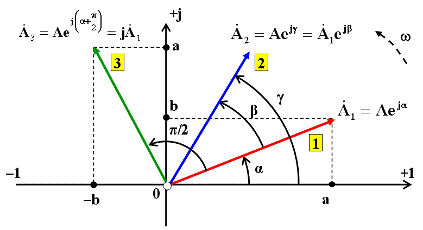
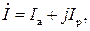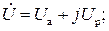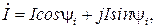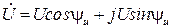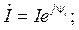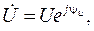От векторного представления синусоидальных функций переходят к их выражению в виде комплексных функций <комплексных чисел),изображая векторы в комплексной плоскости с осями координат: Re — ось действительных чисел и величин и 1ш — ось мнимых чисел и величин.
Отложим, например, вектор амплитуды напряжения Um, отображающий синусоидальное напряжение и = Umsin <(Ot +*РМ) (рис. 2.8, а), в плоскости Re—Im длиной Um под углом х ?и к действительной оси (см. рис. 2.8, б).
Примечание. Комплексные величины будем обозначать соответствующей буквой с чертой под ней, например А, С, U, Е, I. Согласно ГОСТ 2.710-81 для синусоидально изменяющихся величин, таких как напряжение, ток и т.д., разрешается обозначать их комплексы соответствующей буквой с точкой над ней, т.е. А, С, Ё ,Ё,1.
При этом вектор Цт при t = 0 выражают экспоненциальной функцией с мнимым аргументом и называют комплексной амплитудой, т.е.
При повороте вектора Цт на угол Ш его умножают на оператор вращения е* ш , т.е. при 0
Модуль и аргумент комплексной амплитуды. Запишем соответствие синусоидального напряжения и его комплекса:
где U_m = Ume J4>u — комплексная амплитуда напряжения, не зависящая
от времени (t = 0); j = уГ- = e jn ‘ 2 — мнимая единица; Um и X VU — модуль и аргумент комплексной амплитуды напряжения Um при t = 0; со/ + — аргумент комплекса амплитуды напряжения при t Ф 0. Отметим, что модулем комплексной амплитуды напряжения является амплитуда Um, а аргументом — начальная фаза х ?и синусоидального напряжения u<t).
Итак, вектор амплитуды напряжения, вращающийся с частотой со против хода часовой стрелки в комплексной плоскости Re—Im (см.
рис. 2.8, б), состоит из комплексной амплитуды Um = Ume J ^ u , не зависящей от времени, и множителя e JK>l — оператора вращения, имеющего модуль, равный единице, и аргумент со Г, линейно нарастающий во времени с угловой частотой со.
Умножение вектора Um на множитель e J(01 означает его поворот на угол со/ в положительном направлении (см. рис. 2.8, б), в то время как при его умножении на множитель е
т вектор Цт нужно повернуть на угол со/ по ходу часовой стрелки.
Соотношение между комплексной и временной функциями. Любая точка в комплексной плоскости или вектор, направленный от начала координат к данной точке, изображается комплексным числом А = а + jb, где а — координата точки по оси действительных чисел; b — координата точки по оси мнимых чисел (рис. 2.9, а).
Воспользовавшись формулой Эйлера
запишем координаты комплекса амплитуды напряжения на осях Re и Im комплексной плоскости (см. рис. 2.9, б):
Соотношение (2.10) показывает, что синусоидальная функция напряжения u(t) = f/,„sin(co/ + *РМ) есть проекция вращающегося вектора на мнимую ось или есть мнимая часть (без J) комплексной амплитуды напряжения, так как
а косинусоидальная функция напряжения u(t) = Umcos(wt + *РИ) есть проекция вращающегося вектора на действительную ось или действительная часть комплексной амплитуды напряжения, так как
Например, и = 10sin(otf + 45°) j—»Im[10e y45 °e- /№/ ] = lm[Ume J ], где um = 10И 5 — комплексная амплитуда напряжения.
Поделив комплексную амплитуду напряжения Um на V2, получим комлекс действующего значения напряжения, или комплекс напряжения:
По аналогии записываются комплексы ЭДС Е = Ее^ е и тока / = 1е*‘ ,например
Переход от комплексов к временным функциям. Обратный переход от комплексов к синусоидальным функциям осуществляют следующим образом:
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Изображение синусоидальных функций в комплексной форме
Для анализа и расчета электрических цепей синусоидального тока применяют комплексный метод, базирующийся на теории комплексных чисел.
Любой вектор А на плоскости, проведенный из начала координат и изображающий действующее значение ЭДС, напряжения или тока однозначно определяется точкой, соответствующей концу этого вектора (точка А на рис. 2.6). При этом модуль вектора равен действующему значению (А), а угол между вектором и осью вещественных чисел Яе равен начальной фазе (у/). На плоскости комплексных чисел точке А соответствует одно комплексное число А. Таким образом, любой вектор, проведенный из начала координат, однозначно изображается комплексным числом, соответствующим координатам конца этого вектора. Комплексный метод расчета применим только к цепям с синусоидальными ЭДС, напряжениями и токами, так как только синусоидальные величины можно изображать векторами.
Вектор А имеет вещественную (а) и мнимую (Ь) составляющие:
Координаты точки А могут быть выражены через длину вектора |ОЛ| = А и угол у/ : а = Асозу/, Ь = Аь’ту/. Тогда вектор в комплексном виде
Рис. 2.6. Составляющие ком плексного числа на ком’ плексной плоскости
где 
ОА; 
положительному направлению вещественной оси ( Яе ).
Угол у/ положителен, если он отсчитывается в направлении, противоположном вращению часовой стрелки, и отрицателен, если отсчитывается в направлении вращения часовой стрелки.
Используя формулу Эйлера 
где — поворотный множитель, указывающий, на какой угол по отношению к вещественной оси должен быть повернут вектор, длина которого равна модулю |И|.
Таким образом, поворот вектора ОА на угол ±у/г/2 соответствует умножению его на ± у ; поворот на ± у/г — умножению его на -1 и т.д.
Над комплексными числами, изображающими векторы ЭДС, напряжений и токов, можно производить все алгебраические действия:
• Сложение и вычитание чисел:
а)
Таким образом, сложение и вычитание чисел лучше производить в алгебраической форме, а умножение и деление — показательной форме.
Представим синусоидальный ток в комплексной форме. Мгновенное значение синусоидального тока
можно представить вектор тока / в комплексной форме (рис. 2.7):
где la -1 cosy/j — вещественная часть комплекса тока (активная составляющая тока); Ib — I ‘siruj/i — мнимая часть комплекса тока (реактивная
составляющая тока); 
Пример 2.1. Дано мгновенное значение тока:
Требуется записать вектор тока в комплексной форме. Решение:
В показательной форме:

Рис. 2.7. Вектор синусоидального тока на комплексной плоскости Рис. 2.8. Расположение вектора тока /
В алгебраической форме:
Пример 2.2. Дан вектор тока:
Требуется записать мгновенное значение тока, определить угол у/( между вектором / и вещественной осью и изобразить вектор / графически.
где
Таким образом мгновенные значения тока и у/1:
Табл. 2.1. Синусоидальные функции времени в комплексной форме
 |  |  |  | |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
На рис. 2.8. приведено расположение вектора / на комплексной плоскости в примере 2.
В табл. 2.1. представлены синусоидальные функции времени в комплексной показательной и алгебраической формах для различных аргументов. Использование этих выражений поможет при решении задач в комплексной форме и проведении различных преобразований комплексных чисел.
Видео:ТОЭ 26. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.Скачать

Представление синусоидальных величин вращающимися векторами и комплексными числами
· Представление синусоидальных функций вращающимися векторами
Расчет переменных токов и напряжений с помощью алгебраических операций их мгновенных значений по исходным выражениям (1.1а) − (1.1в) весьма неудобен из-за громоздких вычислений. Графическое представление синусоидальных величин (см. рис.1.3) достаточно наглядно для одной, двух синусоид, но для сложных цепей практически не используется, ввиду трудности построения и анализа нескольких синусоидальных величин.
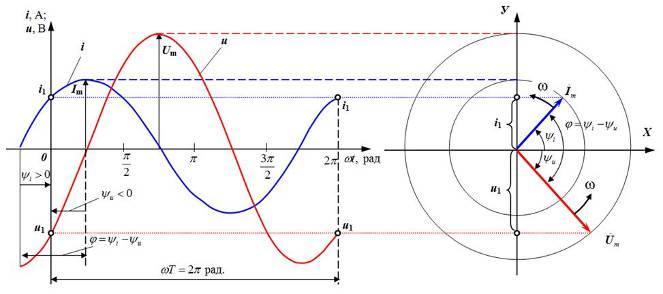
Представления синусоидальных функций при помощи вращающихся векторов (векторных диаграмм), как показано на рис 1.4, позволяет наглядно показать количественные и фазовые соотношения между разными напряжениями, токами и широко используется при объяснении процессов в цепях переменного тока.
Мгновенное значение синусоидальной функции времени t или угла поворота wtможно представить в виде изменяющейся проекции на вертикальную ось вращающегося с угловой скоростью wвектора, как показано на рис 1.4. Векторы, изображающие синусоидальные функции времени, обозначаются, как и комплексные величины, точками вверху. Сравнивая рисунки 1.4,а и 1.4,б, можно видеть что длины векторов 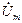
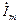
Рис.1.4. Соответствие синусоидальных функций u, i
и вращающихся векторов 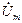
а) – графики мгновенных значений синусоидальных величин напряжения и тока; б)–вращающиеся с угловой скоростью ω векторы 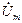
Проекции вращающихся с угловой скоростью ω векторов 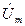
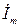
Углы наклона к оси абсцисс Х векторов 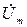
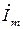
Начальные фазы yu и yi будут соответствовать углам наклона векторов 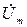
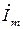
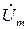
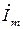
Так как фазовые сдвиги между напряжениями, токами и ЭДС одной частоты w остаются неизменными в течение времени, то от системы вращающихся векторов можно перейти к эквивалентной системе неподвижных векторов для момента времени t = 0.
В электротехнике принято оперировать действующими значениями величин напряжений U , ЭДС Е и токов I. Поэтому длины векторов на векторных диаграммах соответствуют не амплитудным, а действующим значениям, которые, как было выше сказано в 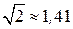
Углы наклона векторов напряжения 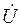
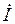
За положительное направление вращения векторов с угловой скоростьюw принято направление вращения против часовой стрелки (см. рис 1.4,б). Первый по вращению вектор считается опережающим следующий за ним вектор нафазовый угол j, который, в свою очередь, считается отстающим на тот же угол j относительно первого вектора. Например, на рис. 1.4,а вектор напряжения 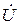
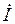
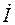
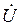
Если для синусоидальных величин одной частоты начальные фазы одинаковы, то векторы этих величин направлены в одну сторону, фазовый угол между ними равен нулю (j=0) и говорят, что эти величины совпадают по фазе (синфазны). Когда для синусоидальных величин разность фаз j = ±p, то векторы этих величин направлены в противоположные стороны и говорят, что эти величины противоположны по фазеили находятся в противофазе.
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, относящиеся к одной цепи, называют векторной диаграммой.
Применение векторных диаграмм делает наглядным анализ электрический цепи. В этом методе сложение и вычитание мгновенных значений синусоидальных величин можно заменить геометрическим сложением и вычитанием их векторов, по правилам, представленным в Приложении 4.
· Представление синусоидальных функций комплексными числами
Применение векторных диаграмм для анализа цепей переменного тока, несмотря на простоту и наглядность, не всегда дает достаточную точность при расчетах. Метод представления синусоидальных функций комплексными величинами и оперирование с ними как с комплексными числами, называемый комплексным методом [1], объединяет в себе простоту векторных диаграмм с возможностью производить расчеты с любой заданной степенью точности.
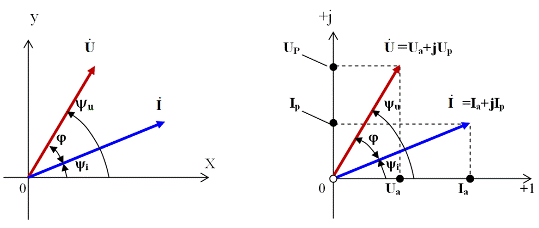
Комплексный метод основан на представлении векторов из декартовой системы координат (рис. 1.5,а) в комплексной плоскости (см. рис. 1.5,б) и на записи их комплексными числами. Это позволяет для цепей синусоидального тока применять законы Ома и Кирхгофа и методы расчета этих цепей в той же форме, что и для цепей постоянного тока, конечно с учетом специфики оперирования с комплексными величинами.
Рис. 1.5. Соответствие векторов и комплексных чисел
а) – векторы действующих значений тока I и напряжения U на векторной диаграмме;
б) – представление векторов тока и напряжения на комплексной плоскости
Синусоидальную функцию тока или напряжения можно однозначно изобразить соответствующим вектором в декартовых координатах (см. рис. 1.5,а) или на комплексной плоскости (рис. 1.5,б). В свою очередь, каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое можно записать в алгебраической, тригонометрической или показательной форме. Например, комплексы тока 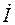
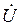
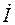
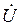
в тригонометрической форме:
и показательной форме:
где 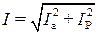
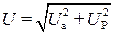
yi = arctgIр/Iа и yu = arctgUр/Uа – аргументы комплексовтока и напряжения, равные их начальным фазам; 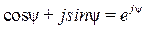
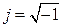
Примечание В электротехнике мнимая единица обозначается буквой j, в отличие от математики, где мнимая единица – i(а в электротехнике i– это принятое обозначение тока).
Таким образом, комплексное число или просто комплекс тока или напряжения в любой из выше перечисленных форм записи является отображением соответствующей синусоидальной функции тока или напряжения.
· Правила операций с векторами и комплексными величинами
Если исходный вектор 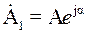
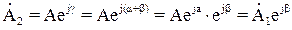
Рис. 1.6. Операция поворота вектора на комплексной плоскости
Следовательно, умножение комплексного числа 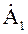
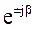
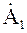
Если угол b = p/2= 90°, то из формулы Эйлера следует:
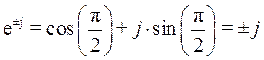
То есть умножение комплексного числа на мнимую единицу ±j соответствует повороту вектора на комплексной плоскости на угол ±p/2.
Если взять, например, комплекс в алгебраической форме 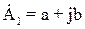
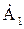
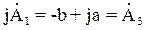
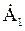
Считая угол поворотного множителя функцией времени, когда b = wt, получаем множитель или оператор вращения 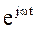
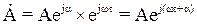
Комплексное число 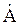
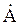
Операции сложения, вычитания, умножения и деления синусоидальных функций времени производят путем тех же алгебраических действий с соответствующими комплексными числами или векторами на комплексной плоскости. Переход от алгебраической формы записи комплексного числа к показательной форме, и наоборот, соответствует переходу от декартовых координат к полярным и от полярных координат – к декартовым. При этом операции алгебраического сложения и вычитания комплексных чисел, записанных в алгебраической форме, заменяются эквивалентными операциями геометрического сложения и вычитания соответствующих комплекс-векторов, записанных в показательной форме. Выбор той или иной формы записи комплексных чисел определяется простотой и удобством оперирования для определенной математической операции. Так, при сложении и вычитании комплексных чисел более удобна алгебраическая форма записи, а при умножении и делении – показательная.
Дата добавления: 2016-04-11 ; просмотров: 8433 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
📽️ Видео
Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Расчет цепей переменного синусоидального тока | Метод комплексных амплитуд | Часть 3Скачать

2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

Изобразить область на комплексной плоскостиСкачать

Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Комплексные числа в электротехникеСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Мнимые числа реальны: #10 Функции комплексных переменных [Welch Labs]Скачать
![Мнимые числа реальны: #10 Функции комплексных переменных [Welch Labs]](https://i.ytimg.com/vi/HwrASWkOYvE/0.jpg)
✓ Комплексные числа. Введение | Ботай со мной #039 | Борис ТрушинСкачать

Лекция 040-2. Комплексные числа. Представление синусоид комплексными числамиСкачать

Сложение, вычитание, умножение и деление комплексных чисел | Высшая математикаСкачать

Комплексные числа: коротко и понятно – Алексей Савватеев | Лекции по математике | НаучпопСкачать

Комплексные числа: начало. Высшая математика или школа?Скачать

Тригонометрическая форма комплексного числаСкачать

Что такое формула Эйлера для комплексных чисел? Душкин объяснитСкачать

Комплексные числа #1Скачать

10 класс, 33 урок, Комплексные числа и координатная плоскостьСкачать