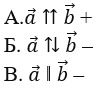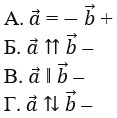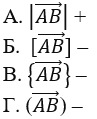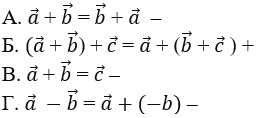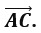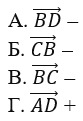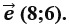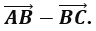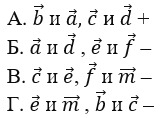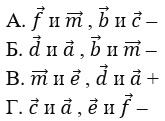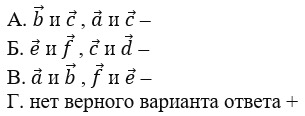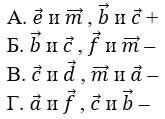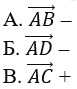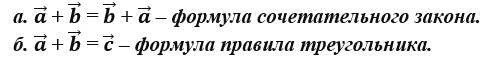Укажите номера верных суждений каждая координата суммы двух векторов

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Ваш ответ

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

решение вопроса

Видео:Скалярное произведение векторов через координаты. 9 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,989
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Векторы укажите номера верных утверждений

Видео:90. Координаты вектораСкачать

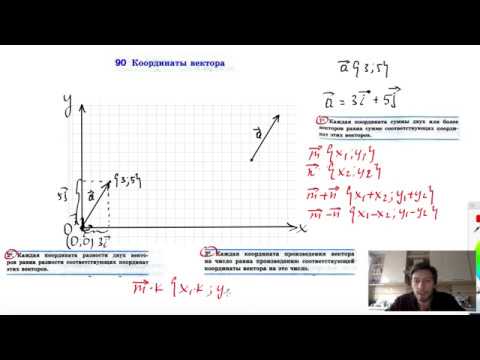
Зачет по теме «Векторы», геометрия, 9 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:9 класс, 2 урок, Координаты вектораСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Любая точка плоскости является вектором.

Векторы называются равными, если их длины равны.

Каждая координата вектора равна сумме соответствующих координат его конца и начала.

Если заданы точки А(2; -3) и В(-6; 7), то точка С(-2; 2) – середина отрезка АВ.

Докажите переместительный закон сложения векторов:

Найдите сумму координат вектора

Определите, при каком значении k векторы и будут коллинеарными.

Треугольник АВС задан координатами своих вершин: А (1; 3),

а) Докажите, что треугольник АВС – прямоугольный.
б) Найдите координаты центра описанной около треугольника окружности и её радиус.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Длина вектора, равного сумме двух векторов, равна сумме длин этих векторов.

Если , то векторы и сонаправлены.

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Если ABCD – ромб, то

Докажите сочетательный закон сложения векторов:

Найдите сумму координат вектора

Определите, при каком значении k векторы и будут коллинеарными.

Треугольник АВС задан координатами своих вершин: А (-4; 1),

б) Найдите длину высоты CD треугольника АВС.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов.

Если треугольник АВС – равносторонний, то .

Если , то векторы и коллинеарны.

Если заданы точки А(2; -3) и В(-6; 7), то вектор имеет координаты .

Пусть M — середина отрезка AB, O — произвольная точка. Докажите, что .

Дано: M — середина AB,

O — произвольная точка.

На чертеже АВС D – параллелограмм, DM = MC , Выразите вектор через векторы и .

Даны точки А(2; 0), В(-1; 3), С (4; 6). Определите координаты вектора

Определите, при каком значении m векторы и будут коллинеарными.

Треугольник АВС задан координатами своих вершин: А (1; 3),

а) Докажите, что треугольник АВС – прямоугольный.
б) Найдите координаты центра описанной около треугольника окружности и её радиус.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Если , то О – середина отрезка АВ.

Векторы называются равными, если они сонаправлены и их длины равны.

Если координаты вектора , то координаты вектора.

Если векторы коллинеарны, то они лежат на одной прямой.

Сформулируйте и докажите, используя векторный метод, теорему о средней линии трапеции.

Дано: AB CD — трапеция, MN – средняя линия.

На чертеже АВС D – параллелограмм, BM = MC , Выразите вектор через векторы и .

Даны векторы . Определите координаты вектора

Определите, при каком значении m векторы и будут коллинеарными.

Треугольник АВС задан координатами своих вершин: А (0; 1),

а) Вычислите длину медианы AD треугольника АВС.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Противоположно направленные векторы, имеющие равную длину, называют противоположными.

Если векторы лежат на одной прямой, то они коллинеарны.

Если заданы точки А(2; -3) и В(6; 7), то точка С(2; 5) – середина отрезка АВ.

Каждая координата вектора равна разности соответствующих координат его конца и начала.

Сформулируйте и докажите лемму о коллинеарных векторах.

Доказать: существует k , что

Используя рисунок, выразите вектор через , и

Вычислите длину отрезка АВ, если А (2; 6), В(4, -2).

Определите, при каком значении k точки А, В и С лежат на одной прямой, если и .

Четырехугольник ABCD задан координатами своих вершин:

А (-1; 0), В (-1; 3), С (4; 6), D (4; 0).

а) Докажите, что АВС D – трапеция.

б) Найдите длину её средней линии.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Если длины векторов равны, то равны и сами векторы.

Векторы и — коллинеарны .

Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Если АВС D – параллелограмм, то

Сформулируйте и докажите правило, позволяющее по координатам векторов находить координаты их суммы.

Используя рисунок, выразите вектор через , и

Определите, при каком значении k точки А, В и С лежат на одной прямой, если и .

Четырехугольник ABCD задан координатами своих вершин:

А (-2; -3), В (1; 4), С (8; 7), D (5; 0).

а) Докажите, что АВС D – ромб.

б) Вычислите площадь ABCD .

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Длина вектора равна квадратному корню из разности квадратов его координат.

Если АВС D – квадрат, то и — коллинеарны.

Если А(-2; 7) и В(6; -1), то имеет координаты .

Если АВС D – квадрат, то = .

Сформулируйте и докажите правило вычисления координат середины отрезка.

Дано: , С – середина АВ.

По данным рисунка вычислите

Определите, при каком значении k векторы и будут коллинеарными.

а) Пусть АА ₁ , ВВ ₁ , СС ₁ – медианы треугольника АВС. Докажите, что

б) Вычислите координаты точки К пересечения медиан этого треугольника, если А(2; -1), В(2 ;2), С(-3; 5).

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Длина вектора, равного сумме двух векторов, меньше или равна сумме длин этих векторов.

Если , то векторы и коллинеарны.

Каждая координата середины отрезка равна полуразности соответствующих координат его концов.

Если ABCD – ромб, то

Сформулируйте и докажите правило вычисления координат вектора, по известным координатам его начала и конца.

Даны точки А(2; 4), В(-1; 3), С (0; 5). Определите координаты вектора

Определите, при каком значении m векторы и будут коллинеарными.

Четырехугольник ABCD задан координатами своих вершин:

А (-5; 1), В (-2; 4), С (0; 2), D (-3; -1).

а) Докажите, что АВСD – прямоугольник.

б) Вычислите длину медианы ВМ треугольника АВС.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Ненулевые векторы называют коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Если ABCD – ромб, то

Каждая координата середины отрезка равна полуразности соответствующих координат его концов.

Если А(-2; 7) и В(6; 1), то имеет координаты .

Сформулируйте и докажите правило вычисления длины вектора, по его координатам.

Используя рисунок, выразите вектор через , и

AB – диаметр окружности, где А(1; 4), В(-3; 7). Вычислите радиус данной окружности.

Даны векторы . Определите, при каком значении k выполняется равенство

Четырехугольник ABCD задан координатами своих вершин:

А (0; 8), В (-6; 0), С (2; -6), D (8; 2).

а) Докажите, что АВСD – квадрат.

б) Вычислите радиус окружности, описанной около квадрата.

Зачет по теме: «Векторы. Метод координат», 9 класс.

Укажите номера верных утверждений

Каждая координата вектора равна сумме соответствующих координат его конца и начала.

Нулевой вектор считается коллинеарным любому вектору.

Если ABCD – прямоугольник, то , где О – точка пересечения диагоналей.

Сформулируйте и докажите правило вычисления расстояния между точками.

На чертеже АВС D – параллелограмм, BM = MC , Выразите вектор через векторы и .

Даны точки А(2; -5), В(1; 6). Вычислите координаты точки С, если известно что

Определите, при каком значении k точки А, В и С лежат на одной прямой, если и .

Треугольник АВС задан координатами своих вершин: А (-4; 1),

а) Докажите, что треугольник АВС – равнобедренный.

б) Найдите площадь данного треугольника.

Краткое описание документа:

• Укажите номера верных утверждений

• 1. Любая точка плоскости является вектором.
• 2. Векторы называются равными, если их длины равны.
• 3. Каждая координата вектора равна сумме соответствующих координат его конца и начала.
• 4. Если заданы точки А(2; -3) и В(-6; 7), то точка С(-2; 2) – середина отрезка АВ.
• 5. Длина вектора, равного сумме двух векторов, равна сумме длин этих векторов.

  6. Если , то векторы и сонаправлены.

  7. Каждая координата середины отрезка равна полусумме соответствующих координат его концов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 316 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 489 104 материала в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

Глава 9. Векторы

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Дистанционные курсы для педагогов

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 24.01.2018 5627 —> —> —> —>
• DOCX 995.4 кбайт —> —>
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Бовина Татьяна Валентиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 80449
• Всего материалов: 15

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Сложение и вычитание векторов через координаты. Практическая часть. 11 класс.Скачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

«Учителя года» проведут открытые занятия для педагогов России

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Ускоренный просмотр онлайн-лекций не мешает их пониманию

Время чтения: 3 минуты

Минпросвещения России запускает конкурс для учителей физкультуры

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Формулы векторов через координаты. Практическая часть. 9 класс.Скачать

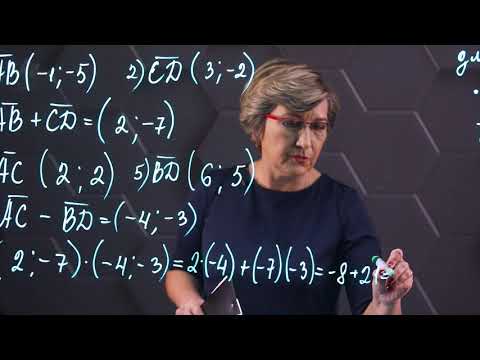
Помогите , пожалуйста ) с решением , если можноданы векторы а с и m укажите верные решения1) вектор а перпендикулярен m2)вектор а не перпендикулярен m3) вектор с перпенди?

Математика | 5 — 9 классы

Помогите , пожалуйста ) с решением , если можно

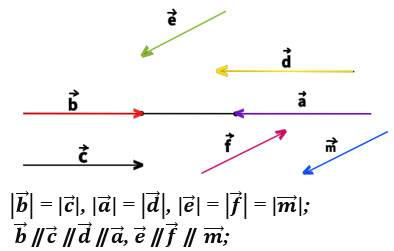
даны векторы а с и m

укажите верные решения

1) вектор а перпендикулярен m

2)вектор а не перпендикулярен m

3) вектор с перпендикулярен m

4) вектор с не перпендикулярен

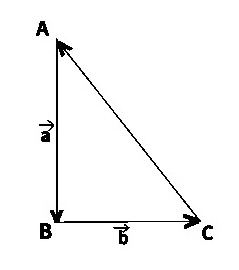
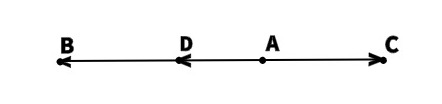
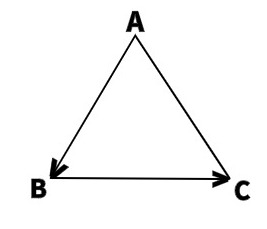
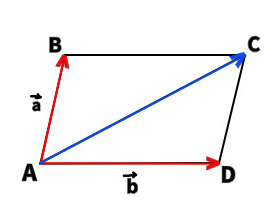
Построили три вектора и сразу видим, что

и 1) и 3) верные выражения.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Вектор m = 6 * (вектор a) + 3 * (вектор b) — 2 * (вектор c) разложен по трем некомпланарным векторам a, b, c?

Вектор m = 6 * (вектор a) + 3 * (вектор b) — 2 * (вектор c) разложен по трем некомпланарным векторам a, b, c.

Разложите вектор b по векторам a, c, m.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Вычислить длину вектора а = (2m — 3n) — (m + n) если даны координаты векторов m = (2 ; 3 ; 1) n = (0 ; 1 ; 1)?

Вычислить длину вектора а = (2m — 3n) — (m + n) если даны координаты векторов m = (2 ; 3 ; 1) n = (0 ; 1 ; 1).

Видео:Сложение, вычитание, умножение на число векторов через координату. 9 класс.Скачать

Найти вектор а = 5m + 3n?

Найти вектор а = 5m + 3n.

Длина вектора m = 1, длина вектора n = корень их 2.

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

При каких значениях m и n векторы A (4 ; n ; 5) Вектор B (3 : 2 : m) Коллинеарны ?

При каких значениях m и n векторы A (4 ; n ; 5) Вектор B (3 : 2 : m) Коллинеарны ?

Видео:Скалярное произведение векторов. 9 класс.Скачать

Дано вектор а — 3 2 вектор в 1 — 1 найдите координаты вектора с длину вектора с длина вектора с равно 2 вектора а минус вектор в?

Дано вектор а — 3 2 вектор в 1 — 1 найдите координаты вектора с длину вектора с длина вектора с равно 2 вектора а минус вектор в.

Видео:9 класс, 18 урок, Скалярное произведение векторовСкачать

! ПОМОГИТЕ ПОЖАЛУЙСТА?

Найдите длину вектора

|вектор а — вектор b|

вектор а = (1 ; — 1 ; — 3), b(2 ; 3 ; 1).

Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Вектора а и в перпендикуляр, найдите значение число p, если а (7 ; — 5)И в ( p ; 15)?

Вектора а и в перпендикуляр, найдите значение число p, если а (7 ; — 5)И в ( p ; 15).

Видео:Профильный ЕГЭ 2024. Векторы. Координатная плоскость. Задача 2Скачать

Найдите скалярное произведение вектора m и n, если |m| = 5 ; |n| = 4 и угол между векторами m и n равен 45°?

Найдите скалярное произведение вектора m и n, если |m| = 5 ; |n| = 4 и угол между векторами m и n равен 45°.

Видео:№934. Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), B (-2; 7);Скачать

Укажите номера верных утверждений?

Укажите номера верных утверждений!

1. Любые 2 коллинеарных вектора сонаправлены.

2. Если длины векторов равны, то векторы равны.

3 . Любая точка может выступать в роли вектора.

Видео:Геометрия 9 класс (Урок№8 - Связь между координатами вектора и координатами его начала и конца.)Скачать

Известно что векторы m = a — b + c, n = a + b — c, p = a + b + c Выразите вектор a через вектора m, n, p?

Известно что векторы m = a — b + c, n = a + b — c, p = a + b + c Выразите вектор a через вектора m, n, p.

Вопрос Помогите , пожалуйста ) с решением , если можноданы векторы а с и m укажите верные решения1) вектор а перпендикулярен m2)вектор а не перпендикулярен m3) вектор с перпенди?, расположенный на этой странице сайта, относится к категории Математика и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

Видео:Геометрия 9 класс (Урок№19 - Скалярное произведение в координатах. Свойства произведения векторов.)Скачать

Векторы укажите номера верных утверждений

Тесты по геометрии 9 класс. Тема: «Векторы»

Правильный вариант ответа отмечен знаком +

1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:

Г. нет верного варианта ответа –

2. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:

3. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:

В. противоположно направленными –

4. Какие слова пропущены в предложении?

Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).

А. сонаправленные; разнонаправленные –

Б. противоположно направленные: сонаправленные –

В. сонаправленные: противоположно направленные +

Г. нет верного варианта ответа –

5. Длиной ненулевого вектора 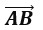называется:

Б. длина отрезка AB +

Г. нет верного варианта ответа –

6. Выберите верное обозначение сонаправленных векторов.

Г. нет верного варианта ответа –

7. Векторы называются равными, если:

А. они коллинеарны –

Б. их длины равны –

В. они сонаправлены –

Г. они сонаправлены и их длины равны +

8. Выберите верное обозначение противоположных векторов.

9. Выберите верное обозначение длины вектора

тест 10.

11. – это формула:

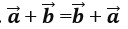
А. разности вектора –

Б. сочетательного закона –

В. нет верного варианта ответа –

Г. переместительного закона +

12. Выберите верную формулу сочетательного закона.

13. Вектор отложен от точки M. Точка M является:

А. концом вектора –

Б. началом вектора +

В. серединой вектора –

Г. нет верного варианта ответа –

14. Если длины двух ненулевых векторов равны, и они противоположно направлены, то они называются:

15. ABC – прямоугольный треугольник, 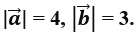Найдите длину вектора

16.

17. Найдите длину вектора

18. Дан правильный треугольник ABC со стороной 2. Найдите длину вектора

Г. недостаточно данных –

19. Выберите пары противоположно направленных векторов.

тест-20. Выберите пары сонаправленных векторов.

21. Выберите пары противоположных векторов.

22. Выберите пары равных векторов.

23. Дан параллелограмм ABCD, AC – диагональ Найдите сумму векторов

Г. нет верного варианта ответа –

24. Выберите верную формулировку правила многоугольника.

А. Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов. +

Б. От любой точки можно отложить вектор, равный данному, и притом только один. –

В. Чтоб сложить два вектора, нужно из произвольной точки отложить один вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало одного с концом второго. –

Г. Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов. –

25. Верны ли следующие суждения?

а. Векторы называются равными, если они коллинеарные и их длины равны.

б. Длиной нулевого вектора 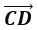является длина отрезка CD.

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

26. Верны ли следующие суждения?

а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.

б. От любой точки можно отложить вектор, равным данному, и притом только один.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

27. Верны ли следующие суждения?

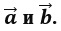
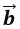
а. Разностью векторов называется такой вектор, сумма которого с вектором равна вектору

б. Два ненулевых вектора называются коллинеарными, если их длины равны и они противоположно направлены.

А. верно только а +

Б. верно только б –

В. оба суждения верны –

Г. оба суждения неверны –

28. Верны ли следующие суждения?

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

29. Верны ли следующие суждения?

а. Вектор называется нулевым, если его начальная и конечная точка совпадает.

б. Модулем вектора называется длина вектора, выраженная числовым выражением.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

тест_30. Верны ли следующие суждения?

а. Скалярные величины характеризуются числом и направлением, а векторные только числом.

б. К векторным величинам относятся скорость, ускорение, перемещение.

Укажите номера.

Задание:

Укажите номера верных утверждений.

1) Скалярное произведение векторов равно произведению их длин на косинус угла между ними.
2) Длина суммы двух векторов равна сумме их длин.
3) Сумма внутренних накрест лежащих углов при пересечении двух параллельных прямых секущей равна 180 градусов.
4) Длина окружности равна ее удвоенному радиусу.
5) Площадь прямоугольника равна его периметру.

Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

Решение:

1) Скалярное произведение векторов равно произведению их длин на косинус угла между ними.
Утверждение верное.

2) Длина суммы двух векторов равна сумме их длин.
Утверждение неверное.

3) Сумма внутренних накрест лежащих углов при пересечении двух параллельных прямых секущей равна 180 градусов.
Утверждение неверное, внутренние накрест лежащие углы при пересечении двух параллельных прямых секущей равны, но в сумме они будут давать 180 градусов, при условии, что секущая перпендикулярна двум данным прямым.

4) Длина окружности равна ее удвоенному радиусу.
Утверждение неверное, так как длина окружности равна произведению удвоенного радиуса на Пи.

5) Площадь прямоугольника равна его периметру.
Утверждение неверное, площадь прямоугольника равна произведению двух его смежных сторон.