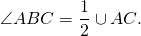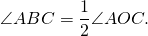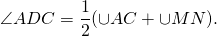Рассмотрим углы в окружности и углы, связанные с окружностью.
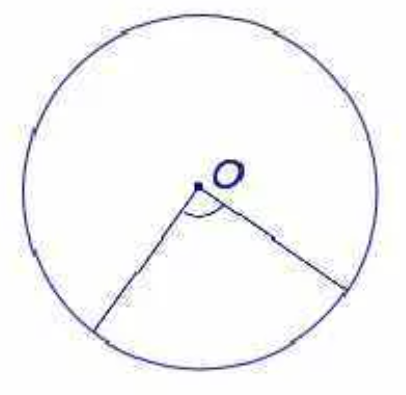
- Угол с вершиной в центре окружности.
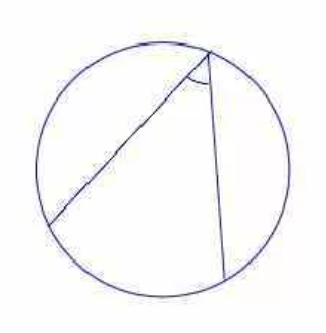
- Угол с вершиной на окружности (его стороны пересекают окружность).
- Угол с вершиной внутри окружности (не в центре).
- Угол с вершиной вне окружности, стороны которого пересекают окружность.
I. Угол с вершиной в центре окружности называется центральным углом.
Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.
Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:
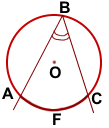
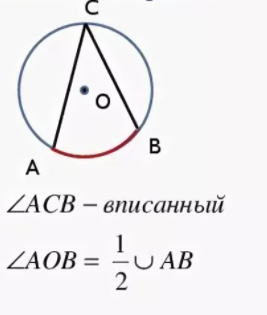
Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.
Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).
Вписанный угол равен половине дуги, на которую он опирается:
Есть другой вариант формулировки свойства вписанного угла.
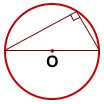
И наоборот: любой прямой вписанный угол опирается на полуокружность.
Другая формулировка этого утверждения:
(обратно: Если вписанный угол прямой, то он опирается на диаметр).
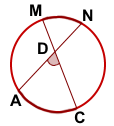
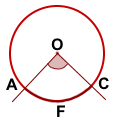
III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.
Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.
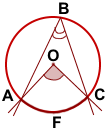
IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.
Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Центральный угол окружности
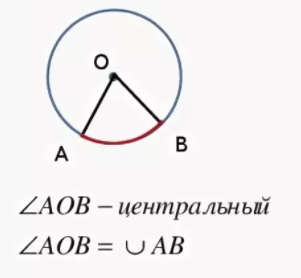
Центральный угол окружности — это угол, образованный двумя радиусами окружности, вершина которого совпадает с центром окружности.
O — центр окружности, AO и OB — радиусы окружности, образующие два центральных угла с вершиной в центре O.
Дуга, лежащая во внутренней области угла, называется дугой, соответствующей этому центральному углу.
Углу AOB соответствует две дуги с концами A и B. Если угол AOB является развёрнутым, то он будет разделять окружность на две равные дуги, называемые полуокружностями:
∠AOB — развёрнутый угол, 

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Градусная мера дуги окружности
Дугу окружности можно измерять в градусах. Градусная мера дуги — это градусная мера соответствующего ей центрального угла.
Если дуга AB окружности с центром O меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла AOB. Если же дуга больше полуокружности, то её градусная мера считается равной 360° —∠AOB:



Сумма градусных мер двух дуг с общими концами равна 360°:


Видео:Углы с вершиной внутри и вне окружности.Скачать

Вписанные и центральные углы, их свойства
теория по математике 📈 планиметрия
Видео:Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать

Вписанный угол
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Свойства вписанных углов
Вписанный угол равен половине дуги, на которую он опирается.
На рисунке показан вписанный угол АСВ и дуга АВ, на которую он опирается. Если, например, дуга АВ=60 0 , то угол АСВ будет равен 30 0 . И наоборот, например, если угол АСВ равен 50 0 , то дуга АВ будет равна 100 0 .
Свойство вписанного угла №2
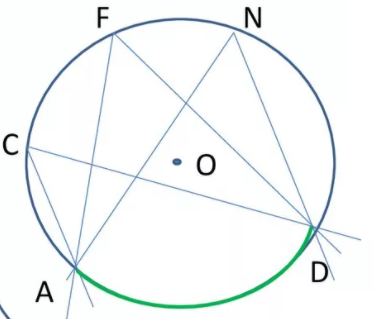
Вписанные углы, которые опираются на одну и ту же дугу, равны.
На рисунке показаны три вписанных угла – ACD, AFD, AND, которые опираются на одну и ту же дугу AD, поэтому эти углы равны.
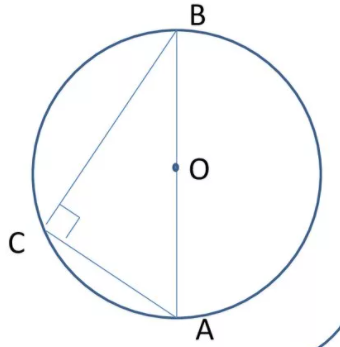
Вписанный угол, который опирается на диаметр, прямой.
На рисунке угол ВСА опирается на диаметр АВ, следовательно, он равен 90 0 .
Видео:Центральный угол в окружностиСкачать

Центральный угол
Центральный угол – это угол, вершина которого лежит в центре окружности.
Свойства центральных углов
Центральный угол равен дуге, на которую он опирается.
На рисунке показан центральный угол АОВ, который опирается на дугу АВ. Например, дуга АВ равна 80 0 , тогда угол АОВ равен также 80 0 . И наоборот, например, если центральный угол АОВ будет равен 70 0 , то и дуга АВ также будет равна 70 0 .
Если центральный и вписанный угол опираются на одну и ту же дугу, то вписанный угол равен половине центрального угла. И наоборот, центральный угол в 2 раза больше вписанного, если они опираются на одну и ту же дугу.
На рисунке показаны вписанный угол АВС и центральный угол АОС, которые опираются на одну и ту же дугу АС. Например, если величина угла АОС равна 120 0 , то величина угла АВС будет равна 60 0 .
🌟 Видео
ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Вписанные и центральные углыСкачать

Центральный и вписанный углыСкачать

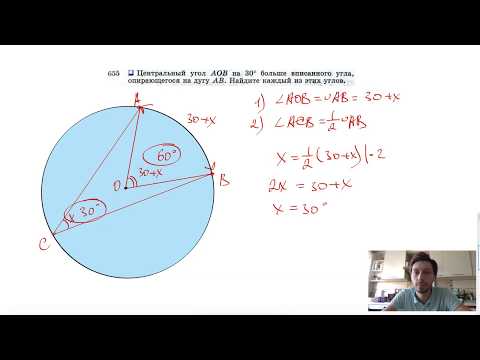
№655. Центральный угол АОВ на 30° больше вписанного угла, опирающегося на дугу АВ. НайдитеСкачать
ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать

Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Вписанный угол равен половине центрального углаСкачать
ГЕОМЕТРИЯ 8 класс : Центральные и вписанные углыСкачать

ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать

Определение величины углаСкачать

УГОЛ И ОКРУЖНОСТЬ: центральный угол, вписанный угол, длина дуги окружностиСкачать

Как понять центральные и вписанные углыСкачать

Решение задач на тему центральные и вписанные углы.Скачать

Углы, вписанные в окружность. 9 класс.Скачать

Вписанные и центральные углыСкачать