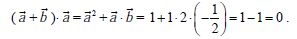Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,997
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Дано: |а| = 1,|b| = 2, ab = 120°. Найдите (а + b) a.
В 4:17 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Дано: |а| = 1,|b| = 2, ab = 120°. Найдите (а + b) a.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Субботина Ландыш Кирилловна — автор студенческих работ, заработанная сумма за прошлый месяц 56 287 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»
Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора
При умножении вектора на число все его координаты
Умножаются на это число, при сложении векторов складываются их соответствующие координаты.
Координаты коллинеарных векторов пропорциональны.
Если A || B, то 
Ответ: 
Найти направляющие косинусы вектора А = .
Направляющие косинусы являются координатами орта (единичного вектора) данного направления.
Найдем модуль вектора А:
Разделив все координаты вектора А на его модуль, получим координаты орта:
Ответ:
Тогда AA + BB + GC = <2A + B— 3G; —A + B+ G; 3A — B+ 2G>, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:
Для векторов A = , B = , C = , D = найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.
C = линейно зависимой или линейно независимой.
Система векторов называется линейно независимой, если равенство
Вычислим главный определитель Δ системы уравнений
По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).
Поскольку других решений нет, данная система векторов линейно независима.
Ответ: Система векторов линейно независима.
Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.
При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?
Для выполнения условия задачи требуется коллинеарность векторов 



Для выполнения условия задачи требуется коллинеарность векторов 



Найдем координаты этих векторов:
Из последней пропорции получаем, что Z = 1 – 2Y. Тогда
Но при этих значениях неизвестных
Условие задачи выполнено.
Используйте определение скалярного произведения:
Используем свойства скалярного произведения:
По определению скалярного произведения
Сложим левые и правые части полученных равенств:
Даны векторы А = и B = . Найти скалярное произведение
Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.
Используем свойства скалярного произведения:
Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.
Ответ: 
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Ответ: K = 
Найти проекцию вектора А = на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.
Используйте свойство направляющих косинусов:
Найдем cosγ: cos260o + cos245o + cos2γ = 1,
Тогда проекция А на заданную ось равна: