Построение треугольника по сторонам

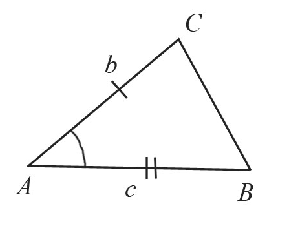
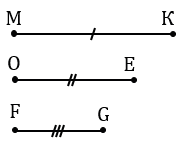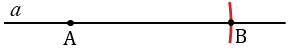Задача:

Построить треугольник по трем его сторонам.

Дано: отрезки МК, ОЕ, FG.

Построить 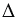АВС так, что АВ = МК, ВС = FG, АС = ОЕ.

Решение:

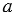
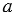
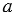
С помощью линейки проводим прямую и на ней с помощью циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой ставим точку А, с помощью циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой обозначаем В.

Далее, с помощью циркуля измеряем отрезок ОЕ и строим окружность с центром в точке А радиуса ОЕ (всю окружность строить необязательно, смотри, выделенное синим цветом).

Далее, с помощью циркуля измеряем отрезок FG и строим окружность с центром в точке B радиуса FG (всю окружность строить необязательно, смотри, выделенное зеленым цветом).

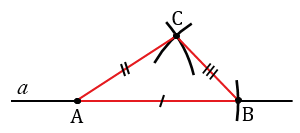
Точку пересечения окружностей с центрами в точках А и В радиусами ОЕ и FG соответственно обозначаем С. Соединяем с помощью линейки точки А и В с точкой С. Получаем треугольник АВС, в котором по построению АВ = МК, ВС = FG, АС = ОЕ, следовательно, 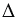АВС — искомый.

Данная задача не всегда имеет решение. Так как для каждого треугольника должно выполняться неравенство треугольника, которое говорит о том, что во всяком треугольнике сумма любых двух сторон больше третьей стороны. Если же какой-нибудь из данных отрезков будет больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.

Поделись с друзьями в социальных сетях:

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Построение треугольника по трем элементам

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Представляем вашему вниманию видеоурок по теме «Построение треугольника по трем элементам». Вы сможете решить несколько примеров из класса задач на построение. Учитель подробно разберет задачу на построение треугольника по трем элементам, а также напомнит теорему о равенстве треугольников.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Связь числа и геометрии. Часть 2. Треугольники. Координаты»

Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать

Построение треугольников. Задачи на построение

Вы будете перенаправлены на Автор24

Решение задач на построение состоит из четырех основных этапов:

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Видео:Построение треугольника по трем сторонам. 7 класс.Скачать

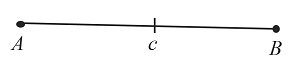
Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

Видео:Построение треугольника по двум сторонам и углу между ними. 7 класс. Геометрия.Скачать

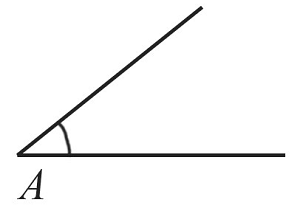
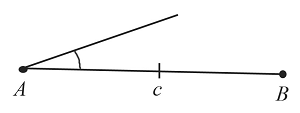
Построение угла, равного заданному

Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить угол, который будет равен углу $А$.

1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Готовые работы на аналогичную тему

Видео:Построение треугольника, равного данномуСкачать

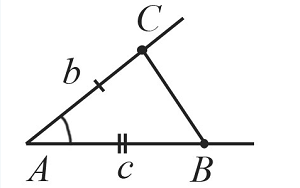
Построение треугольника по двум сторонам и углу между ними

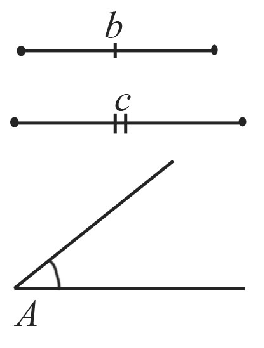
Пусть даны два отрезка $b$ и $с$ и угол $А$:

Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

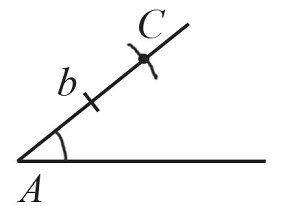
Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

С помощью линейки соединим точки $В$ и $С$.

Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

Видео:Построение треугольника по трем сторонам. 7 класс . Геометрия.Скачать

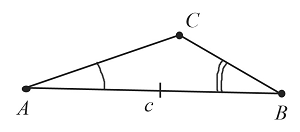
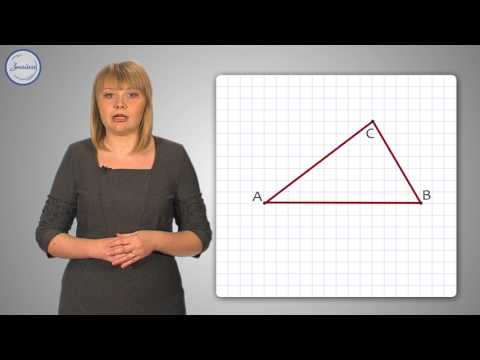
Построение треугольника по стороне и прилегающим к ней углам

Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

Построим угол $А$, который равен заданному, как показано выше.

Построим угол $В$, который равен заданному.

Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Видео:Геометрия 7 класс (Урок№27 - Построение треугольника по трём элементам.)Скачать

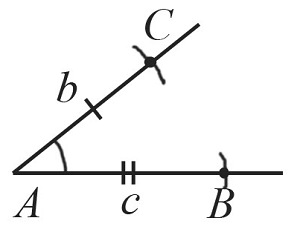
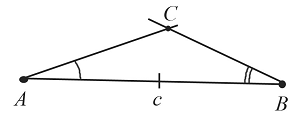
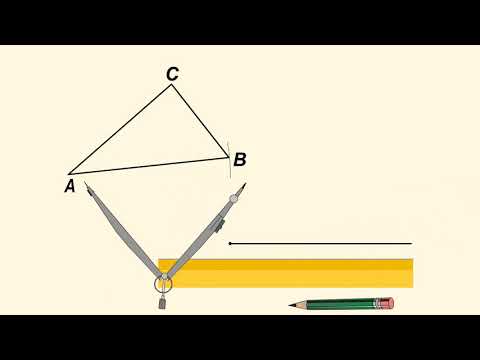
Построение треугольника по трем сторонам

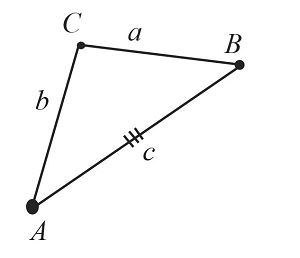
Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

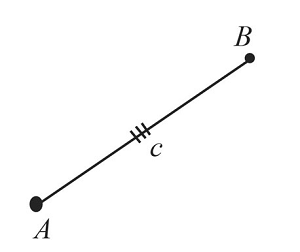
Построим отрезок $АВ$, который равен заданному отрезку $c$.

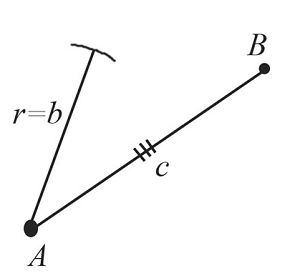
Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

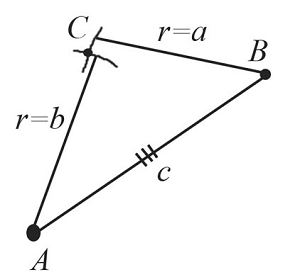
Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

📹 Видео

7 класс, 39 урок, Построение треугольника по трем элементамСкачать

Как построить треугольник по двум сторонам и медиане, проведенной к третьей сторонеСкачать

Геометрия 7 класс. Построение треугольника по трём элементамСкачать

Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Построение треугольника по трем сторонамСкачать

Построение треугольника по трём сторонамСкачать

Построение треугольника по трём сторонамСкачать

Построение треугольника по трем сторонамСкачать

Строим треугольник по стороне и двум углам (Задача 7).Скачать

Построение треугольников по трем элементам | Геометрия 7-9 класс #38 | ИнфоурокСкачать

Построение треугольника по трём сторонам с помощью циркуля и линейки. 5 классСкачать

Построение треугольника по трем элементам. Видеоурок 19. Геометрия 7 классСкачать

ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА ПО ТРЕМ СТОРОНАМ. ЗАДАЧИ НА ПОСТРОЕНИЕ | ГЕОМЕТРИЯ 7 классСкачать