Видео:ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать
Углы в окружности
Рассмотрим углы в окружности и углы, связанные с окружностью.
- Угол с вершиной в центре окружности.
- Угол с вершиной на окружности (его стороны пересекают окружность).
- Угол с вершиной внутри окружности (не в центре).
- Угол с вершиной вне окружности, стороны которого пересекают окружность.
I. Угол с вершиной в центре окружности называется центральным углом.
Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.
Например, центральному углу AOC соответствует дуга AC (или дуга AFC. Обычно дугу называют двумя буквами. Но, поскольку любую из двух, на которые точки A и C делят окружность, можно назвать AC, то третью, дополнительную букву, иногда используют для уточнения выбранной дуги).
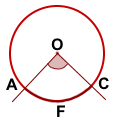
Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:
II. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
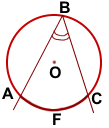
Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.
Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).
Вписанный угол равен половине дуги, на которую он опирается:
Есть другой вариант формулировки свойства вписанного угла.
Вписанный угол равен половине соответствующего ему центрального угла:
Вписанный угол, опирающийся на полуокружность — прямой.
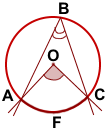
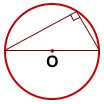
И наоборот: любой прямой вписанный угол опирается на полуокружность.
Другая формулировка этого утверждения:
(обратно: Если вписанный угол прямой, то он опирается на диаметр).
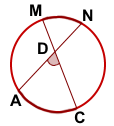
III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.
Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.
IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.
Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Углы, связанные с окружностью
 Вписанные и центральные углы |
| Углы, образованные хордами, касательными и секущими |
| Доказательства теорем об углах, связанных с окружностью |
Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:Вписанные и центральные углыСкачать
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  | | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
|
| Формула: |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
| Формула: |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
|
| Формула: |
| Угол, образованный касательной и секущей касательной и секущей |
| Формула: |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
| Формулы: |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Центральный и вписанный углыСкачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
В этом случае справедливы равенства
и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
В этом случае справедливы равенства
что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8.
Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9.
Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10.
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11.
Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12.
Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать  Центральный угол окружностиЦентральный угол окружности — это угол, образованный двумя радиусами окружности, вершина которого совпадает с центром окружности.
O — центр окружности, AO и OB — радиусы окружности, образующие два центральных угла с вершиной в центре O. Дуга, лежащая во внутренней области угла, называется дугой, соответствующей этому центральному углу.
Углу AOB соответствует две дуги с концами A и B. Если угол AOB является развёрнутым, то он будет разделять окружность на две равные дуги, называемые полуокружностями:
∠AOB — развёрнутый угол, Видео:Геометрия 8 класс (Урок№26 - Градусная мера дуги окружности. Центральные углы.)Скачать  Градусная мера дуги окружностиДугу окружности можно измерять в градусах. Градусная мера дуги — это градусная мера соответствующего ей центрального угла. Если дуга AB окружности с центром O меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла AOB. Если же дуга больше полуокружности, то её градусная мера считается равной 360° —∠AOB:
Сумма градусных мер двух дуг с общими концами равна 360°:
💥 ВидеоВписанные и центральные углыСкачать  ГЕОМЕТРИЯ 8 класс : Центральные и вписанные углыСкачать  8 класс, 33 урок, Градусная мера дуги окружностиСкачать  ЦЕНТРАЛЬНЫЙ угол ВПИСАННЫЙ угол окружности 8 класс АтанасянСкачать  Длина дуги окружности. 9 класс.Скачать  Решение задач на тему центральные и вписанные углы.Скачать  8 класс. Углы в окружностиСкачать  УГОЛ И ОКРУЖНОСТЬ: центральный угол, вписанный угол, длина дуги окружностиСкачать  ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ . §9 геометрия 8 классСкачать  ОГЭ по математике. Треугольник вписан в окружность . (Вар. 4) √ 17 модуль геометрия ОГЭСкачать  Центральные и вписанные углы. Всё про углы в окружностиСкачать  ЕГЭ геометрия ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫСкачать  |
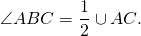
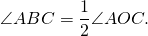
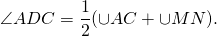
ALB и 