Золотой треугольник соотношение сторон

Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…

Видео:Соотношение сторон треугольника 30-60-90 (доказательство)Скачать

Что такое золотое сечение и как его понимать

Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.

О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.

Сохранившиеся постройки древности тоже подчинены правилу золотого сечения

Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.

Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.

Принцип и формула золотого сечения

На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.

Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.

Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.

Видео:Задача про соотношение сторон. Геометрия 7 класс.Скачать

Как построить прямоугольник с идеальными пропорциями

Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.

Построение прямоугольника с золотым сечением

Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).

Это явно неспроста. Хотя далеко не все подчиняется этой закономерности

Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.

Видео:Золотой треугольникСкачать

Как разделить отрезок по правилу золотого сечения

Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Ничего особенного, но взгляд не оторвать. Знаете почему?

Итак, порядок деления отрезка по правилу золотого сечения:

• Берем отрезок, делим его пополам.
• Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
• Полученную точку C соединяем прямой с другим концом отрезка (A).
• На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
• Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
• Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.

Деление отрезка на участки с идеальным соотношением

Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.

Видео:Золотой треугольник | Олимпиадная математикаСкачать

Идеальный треугольник и пентаграмма

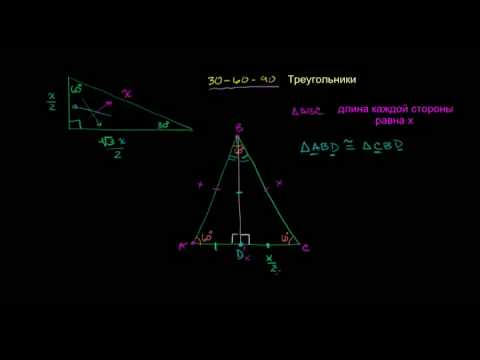
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

• Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
• Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

Построение пентаграммы

• Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
• Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.

Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

Видео:Золотой треугольник - главный источник МЕТАМФЕТАМИНА в Азии | Vice на русскомСкачать

Применение в строительстве

Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Исаакиевский собор — можете посчитать ради интереса

Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.

Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно

Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.

Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное

По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Золотое соотношение во внутреннем оформлении

Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:

• Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
• Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
• При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
• При выборе цвета придерживайтесь примерно тех же правил:
  • Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
  • Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.

    Пример подбора цвета по правилам правильной пропорциональности

• При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.

Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Пропорциональность — важная вещь

Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.

Видео:Золотой треугольник, серебряный треугольникСкачать

Золотое сечение в ландшафтном дизайне

При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

Правило треугольника в садовом дизайне

От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.

Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.

Видео:7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать

Золотой треугольник соотношение сторон

Видео:ТРИЕДИНСТВО ЗОЛОТОГО ТРЕУГОЛЬНИКА. ПРАКТИКА.Скачать

Исследовательские работы и проекты

Видео:Золотой треугольник в бинаре, как удваивать доходы не напрягаясь. Пакеты Family 3 и Family 5 #advantСкачать

Золотое сечение и золотой треугольник

Видео:Золотой и Серебряный треугольник ( устно считать стороны в треугольнике)Скачать

1. Золотое сечение

Тайну золотого сечения пытались осмыслить Платон, Евклид, Пифагор, Леонардо да Винчи, Кеплер. Созданное давно Золотое сечение до сих пор волнует умы многих ученых.

Пифагор считал, что мир устроен по строгим геометрическим законам и в основе мироздания лежит число. Есть предположения, что он свое знание золотого деления позаимствовал у египтян и вавилонян. Об этом свидетельствуют пропорции пирамиды Хеопса, храмов, предметов быта и украшений из гробницы Тутанхамона.

Одной из задач древних было деление отрезка на 2 равные части так, чтобы длина большего отрезка, относилась к длине меньшего так же, как длина всего отрезка к длине большего.

Или эту пропорцию можно перевернуть и найти отношение меньшего к большему .В результате вычислили, что отношение большего к меньшему = 1,61803…, а меньшего к большему = 0,61803…

В Древней Греции такое деление называлось гармоническим отношением. В 1509 году итальянский математик, монах Лука Пачоли написал целую книгу «О божественной пропорции».

Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

2. Золотой треугольник и пентаграмма

«Золотой» треугольник — это равнобедренный треугольник, отношение боковой стороны к основанию равно 1,618 (приложение 1).

Золотое сечение можно увидеть и в пентаграмме — так называли греки звездчатый многоугольник.

Пятиугольник с прочерченными диагоналями, образующими пятиконечную звезду, назвался пентаграммой, которая считалась с древнейших времен почитаемой фигурой.

Это был древний магический знак добра, и братства пяти начал, лежащих в основе мира-огня, земли, воды, дерева и металла. Пентаграмма-правильный пятиугольник, на каждой стороне которого построены равнобедренные треугольники, равные по высоте.

Пятиконечная звезда очень красива, недаром ее помещают на свои флаги и гербы многие страны. Совершенная форма этой фигуры радует глаз.

Пятиугольник буквально соткан из пропорций, и прежде всего золотой пропорции (приложение 2).

Видео:Золотое Сечение наглядно - простой способСкачать

Исследование золотых фигур

Разделы: Математика

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа

В жизни каждого человека присутствует математика. Она используется в самых разнообразных профессиях – математика нужна инженеру, военному, биологу, художнику, можно сказать, что она нужна всем. Великий художник Леонардо да Винчи был один из тех, кто заинтересовался знаменитым золотым сечением. Он много внимания уделял изучению золотого деления. Производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении; поэтому он дал этому делению название золотое сечение.

Золотое сечение интересно тем, что оно позволяет показать связь математики с другими науками, с искусством. А также помогает исследовать золотой треугольник и золотую пирамиду; рассмотреть геометрические задачи, связанные с золотыми фигурами.

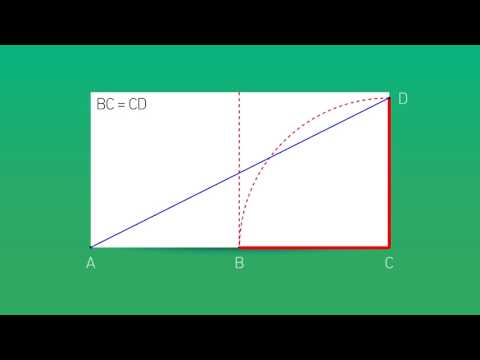
Золотое сечение – это деление отрезка на две части. Таким образом, что большая его часть относится к меньшей части как весь отрезок относится к большой части.

Рис. 1.

= или , откуда

Иногда золотым сечением называют отношение, к , которое обозначают буквой φ:

Число, обратное φ обозначают Ф:

Ф=

Отметим некоторые равенства, связывающие Ф и φ , которые нам впоследствии пригодятся:

1-Ф, 1+Ф=

История золотого сечения.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне и они были известны только посвященным.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

ЗОЛОТОЙ ПРЯМОУГОЛЬНИК.

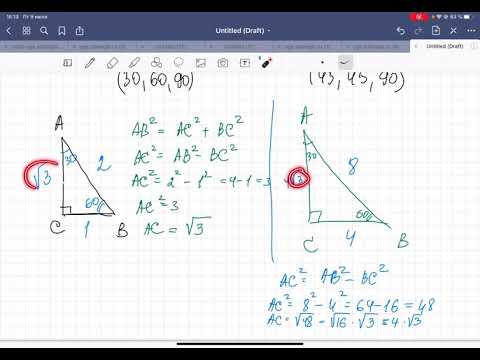
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.

Чтобы убедиться в этом, заметим, что по теореме Пифагора

Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD − квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.

Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению.

ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЕГО ИССЛЕДОВАНИЕ.

Золотым треугольником будем называть равнобедренный треугольник, отношение основания которого к боковой стороне равно φ Одним из таких треугольников является треугольник с боковой стороной Ф и основанием 1; именно его мы в дальнейшем будем называть золотым. Проведем исследование золотого треугольника.

Углы золотого треугольника.

В треугольнике АВС выберем на стороне ВС точку D так, чтобы АD=1 (такую точку легко построить, проведя окружность с центром в точке А и радиусом АС). Из подобия треугольников АВС и АDС получаем:

или , откуда DС=

Поскольку ВС=Ф, DС=φ, то, учитывая равенство Ф=, получаем, что BD=1 и треугольник ABD равнобедренный. Значит, АD- биссектриса треугольника АВС. Теперь легко найти углы треугольника АВС:

5,

В последствии нам встретятся выражения, содержащие и , поэтому вычислим их значения и для удобства выразим через Ф:

=.

Найдем в золотом треугольнике:

1. медиану, проведенную к боковой стороне;
2. высоту, проведенную к основанию;
3. площадь;
4. высоту, проведенную к боковой стороне;

Пусть треугольник АВС − золотой. Для нахождения медианы воспользуемся формулой ,

где

.

Найдем высоту ВН: ВН=Ф

Площадь треугольника АВС будет равна: S=

Пусть – высота, проведенная к стороне ВС. Возьмем на стороне ВС точку так, чтобы . Треугольники АС и АВС подобны с коэффициентом подобия Ф, поэтому

Применение золотого треугольника при решении задач.

Найти длины диагоналей правильного 10-угольника со стороной, равной 1.

Решение. Правильный 10-угольник имеет 4 вида диагоналей, на рисунке показано по одному представителю этих четырех множеств. Найдем их длины. Проще всего найти длину отрезка AF. Для этого найдем величину внутреннего угла правильного 10-угольника: . Теперь легко заметить, что 10-угольник состоит из 10 золотых треугольников, которые имеют общую вершину О ─ центр 10-угольника. Значит, длина диагонали AF равна 2Ф.

Найдем длину диагонали АС. Из треугольника АВС имеем:

= 22) =2(1+)= 4= 2+Ф,

откуда АС=

Найдем длину диагонали AD. В равнобоковой трапеции АВСD углы при основании равны Нетрудно получить, что проекции отрезков АВ и СD на основании AD будут равны .

AD=.

Длину диагонали АЕ можно найти разными способами.

Способ 1. Будем искать ее из треугольника AEF. В этом треугольнике медиана ЕО равна половине стороны AF, поэтому треугольник AEF-прямоугольный. Тогда АЕ= AF

Способ 2. Заметим, что высота золотого треугольника EOF является средней линией треугольника AEF. Поскольку эта высота равна , то АЕ=

Ответ: 2Ф, ,

ЗОЛОТАЯ ПИРАМИДА И ЕЕ ИССЛЕДОВАНИЕ.

Пирамида называется золотой, если каждая её грань − золотой треугольник.

Исследование золотой пирамиды.

Различные способы нахождения объёма золотой пирамиды.

I способ: объем пирамиды находим по формуле . Для этого нам необходимо вычислить высоту пирамиды.

Пусть DABC-данная пирамида,DH − ее высота. Плоскость ADH пересекает ребро ВС в точке М, причем ВМ=СМ. Треугольник ADM − равнобедренный.

Опустим на его основание AD высоту МК. Из подобия треугольников AHD и AKM будем иметь:

.

Поставим в это равенство известные нам числа:

МК= (расстояние между ребрами AD и ВС),

АМ= (высота золотого треугольника):

DH=. А т.к. =.

II способ:

длины противоположных ребер, расстояние между ними, – угол между ними;

=.

III способ:

Объем золотой пирамиды – это объем прямоугольного параллелепипеда минус объем четырех маленьких пирамид с ребрами длиной 1,, и , значит:

Применение золотой пирамиды при решении задач.

Найдем площадь поверхности золотой пирамиды.

= = 4

Золотое сечение в картине Леонардо да Винчи «Джоконда»

Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

Золотая спираль в картине Рафаэля «Избиение младенцев»

В отличии от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре – спирали. Многофигурная композиция, выполненная в 1509 – 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру» Избиение младенцев». На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции −точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, − вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается . золотая спираль! Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.

Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции » Избиение младенцев» или только»чувствовал» её. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел.

Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, − в левой части композиции и лежащее тело ребенка − в ее центре.

Нельзя не увидеть золотой треугольник и золотую пирамиду в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Но эти замечательные тела еще и потому красивы, что в основе их пропорциональных линий лежит золотая пропорция. Многие материалы, и не только драгоценные камни, состоят из мельчайших частиц, которые имеют форму многогранника. Такие вещества называются кристаллами. Соль, лед, песок, графит и т. д. состоят из кристаллов. Внутреннее устройство кристалла представляется в виде кристаллической решетки, в ячейках которых размещены по законам симметрии одинаковые мельчайшие частицы.

Литература:

1. Большая Российская энциклопедия. М., «Научное издательство», 2007.
2. Т. Каменева, А. Козлов. Золотой треугольник в задачах. М., 2007.
3. Журнал «Математика в школе», 1993, № 3.
4. Ковалев Ф.В. Золотое сечение в живописи. К.: Высшая школа, 1989.
5. «Математика – Энциклопедия для детей» М.: Аванта +, 1998.
6. Волошинов А.В. «Математика и искусство». М.: Мир, 1979.

💥 Видео

Лучший Способ Найти Себя / Как Работает Золотой Треугольник ПроцветанияСкачать

Правило Золотого треугольника (простые советы) Владимир МурановСкачать

золотой треугольникСкачать

Что такое «Золотой Треугольник»? Ловушки для ПокупателейСкачать

Правило Золотого Треугольника. Мерчендайзинг. Размещение товаров. Маркетинговое правилоСкачать

Что такое "Классика" и "Бинар". Премия 100$ для новичка. Золотой треугольник.Скачать

Зачем нужен золотой треугольник? #livegood #livegood #livegoodcompanyСкачать