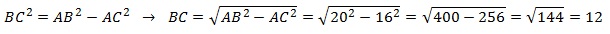Ab 16 bc 12 длина окружности

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Окружность, круг и их элементы

В 17 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.

По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.

Ответом в задании 17 является целое число или конечная десятичная дробь.

Теория к заданию №17

Несмотря на то, что в задании №17 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».

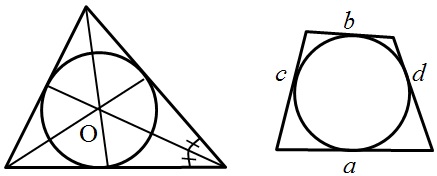
Начнем рассмотрение с понятия вписанная окружность:

1. Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
2. Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d

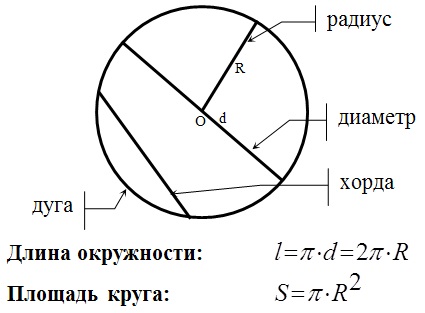
Длинна окружности и площадь:

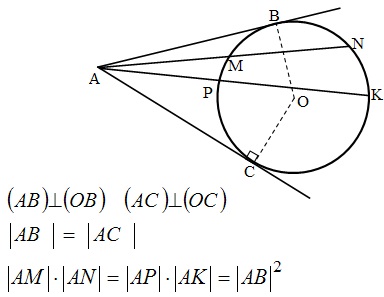
Касательная и секущая:

• Касательная – прямая, имеющая с окружностью одну общую точку.
• Секущая – прямая, имеющая с окружностью две общие точки.

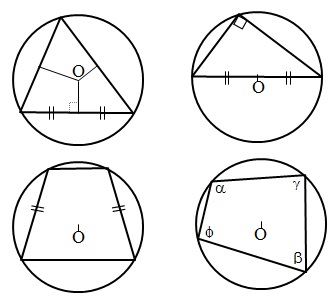
Описанная окружность и её свойства:

1. Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
2. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
3. Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
4. Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.

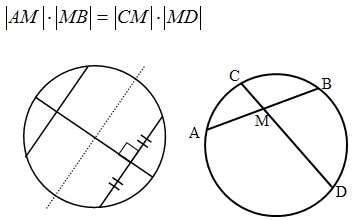
Хорда – отрезок, соединяющий две точки окружности.

• Диаметр, делящий хорду пополам, перпендикулярен хорде.
• В окружности равные хорды равноудалены от центра окружности.
• Отрезки пересекающихся хорд связаны равенством:

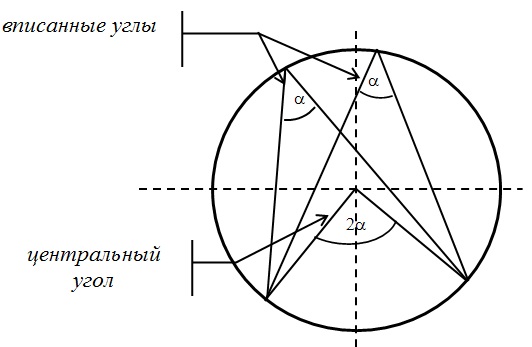
Центральный и вписанный углы:

Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.

Разбор типовых вариантов заданий №17 ОГЭ по математике

Первый вариант задания

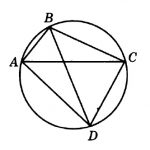
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.

Решение:

Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:

∠ABD = 92 — 60 = 32

Второй вариант задания

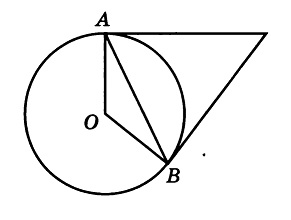
Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.

Решение:

Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:

Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.

Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:

Третий вариант задания

В треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.

Решение:

Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.

По теореме Пифагора найдем гипотенузу AB:

AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400

Гипотенуза равна 20, значит радиус — 10.

Демонстрационный вариант ОГЭ 2019

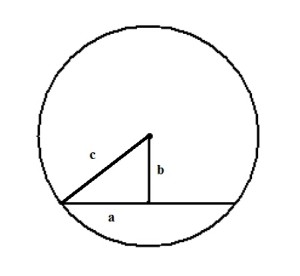
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.

Решение:

Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:

Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a:

a² = c² — b² = 13² — 5² = 169 — 25 = 144

Но а — лишь половина хорды, поэтому вся хорда равна 2 • а = 24

Четвертый вариант задания

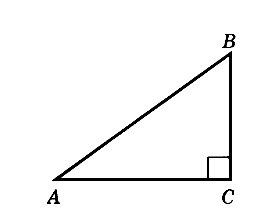
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 10. Найдите ВС, если АС=16.

Решение:

Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90 0 , и, следовательно, ∆АСВ прямоугольный.

Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора

АС 2 +ВС 2 =АВ 2 (1)

По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20.

Тогда из (1) получим:

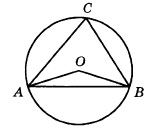
Пятый вариант задания

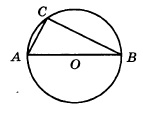
Треугольник АВС вписан в окружность с центром в точке О. Найдите угол АСВ, если угол АОВ равен 113 0 . Ответ дайте в градусах.

Решение:

Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113 0 .

Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=113 0 , то угол АСВ равен

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Найдите длину окружности и площадь круга, если АВ — диаметр окружности, а хорды АС и ВС равны 12 см и 9 см.

Видео:Длина окружности. Математика 6 класс.Скачать

Ваш ответ

Видео:Длина окружности. Практическая часть. 9 класс.Скачать

решение вопроса

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,929
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

📸 Видео

Длина окружности. Практическая часть. 9 класс.Скачать

Длина окружности. 9 класс.Скачать

+Как найти длину окружностиСкачать

Как измерить длину окружностиСкачать

Длина дуги окружности. 9 класс.Скачать

Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

9 класс, 26 урок, Длина окружностиСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Длина окружности и площадь кругаСкачать

Длина окружности. Площадь круга.Скачать

ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать