Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.
- Поворот точки вокруг точки
- Полный оборот
- Угол поворота
- Направление поворота
- Величина угла поворота, угол произвольной величины
- Поворот фигуры вокруг точки на угол
- Алгебра и начала математического анализа. 10 класс
- Как найти угол поворота формула
- Вращательное движение, характеристики
- Угол поворота
- Соотношение между единицами угла
- Число оборотов
- Период
- Угловое перемещение
- Угловая скорость
- Угловая скорость
- Нормальное ускорение
- Тангенциальное ускорение
- Угол поворота
- Соотношение между единицами угла
- Число оборотов
- Период
- Угловое перемещение
- Угловая скорость
- Равномерное движение тела по окружности
- Равномерно ускоренное движение по окружности без начальной угловой скорости
- Равномерно ускоренное движение по окружности с начальной угловой скоростью
- Неравномерно ускоренное движение тела по окружности
- Мгновенная угловая скорость
- Средняя угловая скорость
- Вращательное движение тела, формулы
- Векторные величины, характеризующие вращательное движение тела
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Поворот точки вокруг точки
Центр поворота – точка, относительно которой осуществлен поворот.
Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .
Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.
Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .
Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Полный оборот
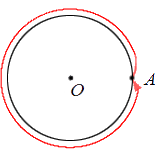
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .
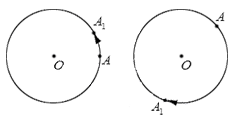
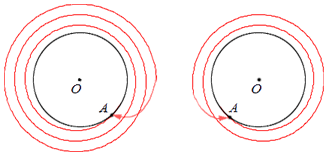
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:
В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.
Видео:Физика - движение по окружностиСкачать

Угол поворота
Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.
Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.
Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .
Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .
Разберем характеристики угла поворота подробнее.
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Направление поворота
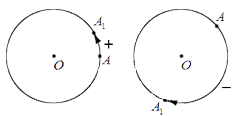
Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.
Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.
Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.
Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Величина угла поворота, угол произвольной величины
Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.
Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;
Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.
Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.
Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.
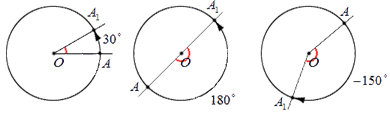
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :
Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:
Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.
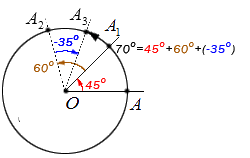
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:
Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .
По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .
Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.
В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.
При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .
Видео:Вращательное движение. 10 класс.Скачать

Поворот фигуры вокруг точки на угол
Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).
Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.
Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №29. Радианная мера угла
Перечень вопросов, рассматриваемых в теме:
1) Понятие тригонометрической окружности;
2) Поворот точки вокруг начала координат;
3) Длина дуги окружности и площадь кругового сектора.
Глоссарий по теме
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Теоретический материал для самостоятельного изучения
На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.
На окружности можно выделить дугу. А если рассмотреть круг — часть плоскости, ограниченной окружностью — то можно выделить круговой сектор.
«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)
Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, 

Вычислите длину каждой дуги.
Ответ. длина каждой дуги равна 
Длина полуокружности равна 


Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.


Длину дуги l окружности радиуса R (рис.4)
можно вычислять по формуле
А площадь S кругового сектора радиуса R и дугой 
находят по формуле: 

Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
Введём понятие поворота точки. (рис.2)
- Пусть
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
- Пусть
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол 
угол 
Примеры и разбор решения заданий тренировочного модуля
Найти градусную меру угла, равного 
Решение: Используя формулу (1),
находим 
Так как 


Ответ: 
Пример 2. Найти радианную меру угла, равного 60
Вычисляем по формуле (2): 

При обозначении мер угла, наименование «рад» опускают.
Ответ: 

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера 
Решение: Используя формулу (3),
получим:
Ответ: 
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла 
По формуле (4) вычисляем
Ответ: 45 
Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный 
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как 
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны 
На окружности можно найти координаты любой точки.
Ответ:
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Как найти угол поворота формула
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Видео:Тригонометрическая окружность. Как выучить?Скачать

Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Видео:ДВИЖЕНИЕ ПО ОКРУЖНОСТИ: угол поворота и угловая скорость. Ускорение при равномерном движении.Скачать

Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
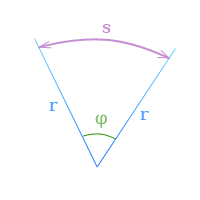
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
( 1 рад = 1 м/ 1 м = 1 ), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). 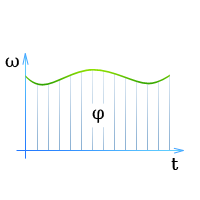
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Видео:Радианная мера угла. 9 класс.Скачать

Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Видео:Угловая скорость и радианная мера углаСкачать

Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) ?,
скорость u — угловая скорость ?,
ускорение a — угловое ускорение ?
Видео:Радиус описанной окружностиСкачать

Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
? — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ? от t). 
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость ? от t) и график углового ускорения (зависимость ? от t).
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
? — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
? — угловая частота,
то
Период
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:
• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Видео:Как искать точки на тригонометрической окружности.Скачать

Равномерное движение тела по окружности
Говорят, что тело движется по окружности равномерно, если его угловая скорость постоянна, т.е. тело за равные промежутки времени поворачивается на один и тот же угол.
? — угловая скорость (постоянная в течение времени t)
? — угловое перемещение
t — время поворота на угол ?
Поскольку на графике угловой скорости площадь прямоугольника соответствует угловому перемещению, имеем:
Постоянная угловая скорость — есть отношение углового перемещения (угла поворота) ко времени, затраченному на это перемещение.
Единица СИ угловой скорости:
Видео:Центростремительное ускорение. 9 класс.Скачать

Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно возрастает.
? — мгновенная угловая скорость тела в момент времени t
? — угловое ускорение, постоянное в течение времени t
? — угловое перемещение тела за время t, (? в радианах)
t — время
Поскольку на графике скорости угловое перемещение равно площади треугольника, имеем:
Поскольку вращение тела начинается из состояния покоя, изменение угловой скорости ?? равно достигнутой в результате ускорения угловой скорости ?. Поэтому формула принимает следующий вид:
Видео:Линейная и угловая скорости при равномерном движении по окружностиСкачать

Равномерно ускоренное движение по окружности с начальной угловой скоростью
Начальная скорость тела, равная ?0 в момент t = 0, изменяется равномерно на величину ??. (Угловое ускорение при этом постоянно.)
?0 — начальная угловая скорость
? — конечная угловая скорость
? — угловое перемещение тела за время t в радианах
t — время
? — угловое ускорение постоянное в течение времени t
Поскольку на графике скорости угловое перемещение соответствует площади трапеции под кривой скорости, имеем:
Так как площадь трапеции равна сумме площадей образующих ее треугольника и прямоугольника, получаем:
Далее из графика скорости следует
Совместив формулы мы получим
После преобразования получаем выражение, не содержащее времени:
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Неравномерно ускоренное движение тела по окружности
Движение тела по окружности будет неравномерно ускоренным, если изменение угловой скорости происходит не пропорционально времени, т. е. если угловое ускорение не остается постоянным. В этом случае и угловая скорость и угловое ускорение являются функциями времени.
Связь величин ?, ? и ? представлена на соответствующих графиках.
Мгновенная угловая скорость
Полный угол поворота тела в любой момент времени можно определить по графику углового перемещения. Чем круче график, тем больше в данный момент времени мгновенная угловая скорость.
? — угол между касательной и осью времени t
? — мгновенная угловая скорость
? — угловое перемещение к моменту времени t

Мгновенной угловой скоростью называется первая производная функции ? = ?(t) по времени.
Обратите внимание:
1) чтобы вычислить мгновенную угловую скорость ?, необходимо знать зависимость углового перемещения от времени.
2) формула углового перемещения при равномерном движении тела по окружности и формула углового перемещения при равномерно ускоренном движении по окружности без начальной угловой скорости являются частными случаями формулы (2) соответственно для ? = 0 и ? = const.
Из формул следует:
Проинтегрировав обе части выражения, получим
Угловое перемещение есть интеграл по времени от угловой скорости.
Обратите внимание:
Для вычисления углового перемещения ? необходимо знать зависимость угловой скорости от времени.
Средняя угловая скорость
Средняя угловая скорость для некоторого интервала времени
Среднее число оборотов определяется аналогично формуле:
Вращательное движение тела, формулы
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения.
Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями.

Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Векторные величины, характеризующие вращательное движение тела
| Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело. |  |
Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:
Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):
или, если оси вращения перпендикулярны друг другу
Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.






 Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 
 точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.




















































