Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12.Скачать
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники 
и 
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия – 
Отношение площадей этих треугольников есть 
.
4. Треугольники 
и 
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:8 класс, 6 урок, ТрапецияСкачать
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:СЕРЬЁЗНО готовимся к ОГЭ 2024! / Полный прогон задания 17 на ОГЭ по математикеСкачать
Вписанная окружность
Если в трапецию вписана окружность с радиусом 
и она делит боковую сторону точкой касания на два отрезка — 
и 
, то 
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать
Площадь
или 
где 
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать
Биссектриса трапеции
Биссектриса угла трапеции, пересекающая основание, отсекает от трапеции равнобедренный треугольник.
Дано : ABCD — трапеция, AD ∥ BC,
AF — биссектриса ∠BAD.
Доказать : треугольник ABF — равнобедренный.
1) ∠BAF=∠DAF (так как AF — биссектриса ∠BAD по условию)
2) ∠BFA=∠DAF (как внутренние накрест лежащие при AD ∥ BC и секущей AF)
3) Следовательно, ∠BAF=∠BFA
4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку).
Что и требовалось доказать.
Если биссектриса угла трапеции пересекает не основание трапеции, а прямую, содержащую основание, то она отсекает равнобедренный треугольник на продолжении этой прямой.
Таким образом, биссектриса угла трапеции отсекает на ее основании или продолжении основания отрезок, равный боковой стороне:
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равныСкачать
Биссектриса угла трапеции
Рассмотрим задачи, в которых биссектриса угла трапеции делит противоположное основание на отрезки.
Мы уже имели дело с похожей задачей на биссектрису угла параллелограмма, а также рассматривали частный случай для трапеции (когда основание трапеции равно ее боковой стороне, биссектриса трапеции совпадает с ее диагональю).
I. Биссектриса острого угла при большем основании трапеции делит другое основание на отрезки.
1) ∠ BAF= ∠ DAF (так как AF — биссектриса ∠ BAD по условию).
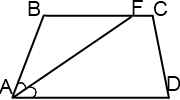
2) ∠ DAF= ∠ BFA (как внутренние накрест лежащие при AD ∥ BC и секущей AF).
3) Следовательно, ∠ BAF= ∠ BFA.
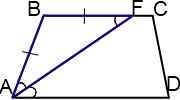
4) Следовательно, треугольник ABF — равнобедренный с основанием AF (по признаку равнобедренного треугольника).
5) Следовательно, AB=BF.
II. Биссектриса тупого угла при меньшем основании трапеции делит другое основание на отрезки.
Аналогично доказывается, что треугольник ABP — равнобедренный:
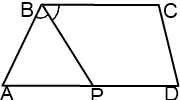
1) ∠ ABP= ∠ CBP (так как BP — биссектриса ∠ ABC по условию).
2) ∠ CBP= ∠ APB (как внутренние накрест лежащие при AD ∥ BC и секущей BP).
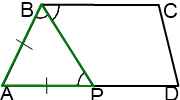
3) Следовательно, ∠ ABP= ∠ APB.
4) Следовательно, треугольник ABP — равнобедренный с основанием BP (по признаку равнобедренного треугольника).
5) Следовательно, AB=AP.
Вывод: в этом случае
биссектриса угла трапеции отсекает от нее равнобедренный треугольник.
Эта задачи — базовые. На их основе существует много других задач.
В следующий раз рассмотрим задачи на пересечение двух биссектрис трапеции.
💡 Видео
Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать
ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать
Задание 25_Признак равнобедренной трапецииСкачать
Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать
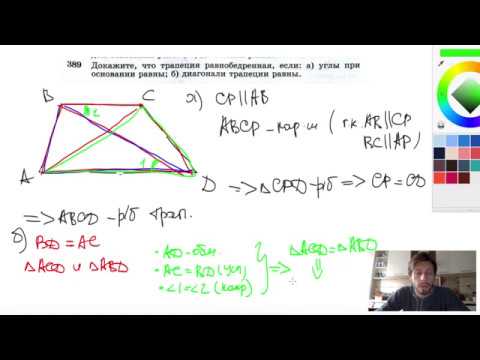
№389. Докажите, что трапеция равнобедренная, если: а) углы при основании равныСкачать
7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать
Трапеция, решение задач. Вебинар | МатематикаСкачать
✓ Свойства и признаки равнобедренного треугольника | Ботай со мной #008 | Борис ТрушинСкачать
ТРАПЕЦИЯ . §8 геометрия 8 классСкачать
Диагонали трапеции и точка их пересеченияСкачать
№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать
Основания равнобедренной трапеции равны 3 и 17 ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать
БИССЕКТРИСА В ТРАПЕЦИИ. Мат в 3 хода!Скачать
