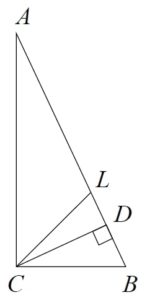
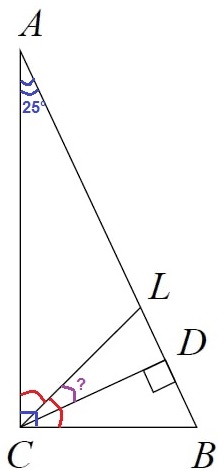
В прямоугольном треугольнике ABC с гипотенузой AB провели высоту CD и биссектрису CL. Найдите величину угла DCL, если ∠CAB = 25°. Ответ дайте в градусах. Запишите решение и ответ.
Источник задания: fioco.ru
Биссектриса CL делит прямой ∠С = 90° пополам, найдём ∠ACL:
∠ACL = 90/2 = 45°
Сумма углов треугольника равна 180°. Найдём в ΔСAL ∠CLA:
∠CLA = 180° – (∠ACL + ∠CAL) = 180° – (45° + 25°) = 110°
Найдём смежный ∠СLD:
∠СLD = 180° – ∠CLA = 180 – 110 = 70°
∠СDL прямой, найдём искомый ∠DCL из ΔDCL:
∠DCL = 180° – (∠СDL + ∠СLD) = 180° – (90° + 70°) = 20°
Видео:Определение длины гипотенузыСкачать

Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
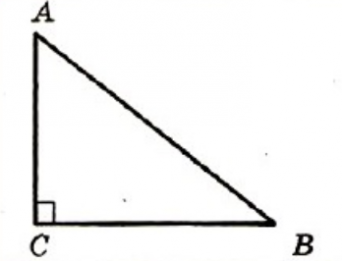
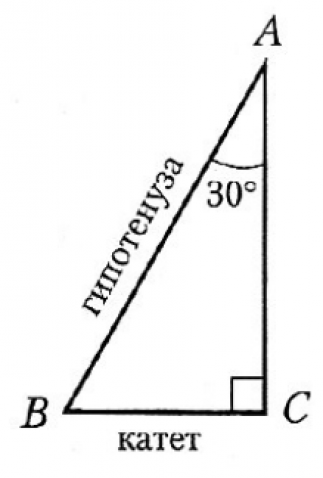
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Видео:Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
- В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .
Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
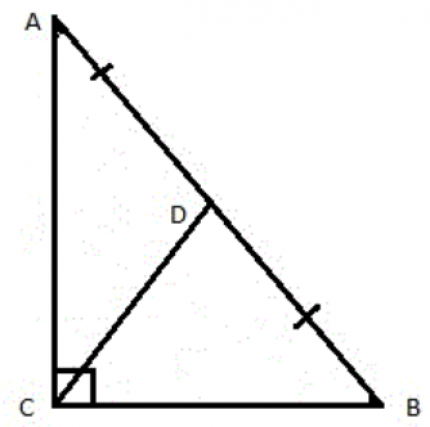
- Медиана, проведенная к гипотенузе, равна её половине.
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Видео:7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Видео:Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.
Египетский треугольник
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.
Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

В прямоугольном треугольнике АВС гипотенуза АВ равна с и?
Геометрия | 5 — 9 классы
В прямоугольном треугольнике АВС гипотенуза АВ равна с и.
В прямоугольном треугольнике АВС
медианы СМ, ВN и АК.
Медиана из прямого угла равна половине гипотенузы
СМ = с / 2 (свойство).
АК = √(АС² + ВС² / 4) = √(4с² * Cos²α + c²Sin²α) / 2 = (c / 2) * √(4 * Cos²α + Sin²α) =
(c / 2) * √(4 * Cos²α + 4Sin²α — 3Sin²α) = c * √(4 — 3Sin²α) / 2.
BN = √(АС² / 4 + ВС²) = √(с² * Cos²α + 4c²Sin²α) / 2 = (c / 2) * √(Cos²α + 4 * Sin²α) =
(c / 2) * √(4Cos²α + 4Sin²α — 3Cos²α) = c * √(4 — 3Cos²α) / 2.
Ответ : СМ = с / 2, АК = c * √(4 — 3Sin²α) / 2, BN = c * √(4 — 3Cos²α) / 2.
Вы находитесь на странице вопроса В прямоугольном треугольнике АВС гипотенуза АВ равна с и? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Ответ : E ∈ α точка Е принадлежит плоскости α ; F ∈ α точка F принадлежит плоскости α ; D ∈ α точка D принадлежит плоскости α ; m ∩ α = E прямая m пересекает плоскость α в точке Е ; FD ⊂ α прямая FD лежит в плоскости α.
Все смотри на фото )).
Длины звеньев ломаной представляют из себя возрастающую геометрическую прогрессию (q>1) значит наибольший отрезок ломаной — пятый : bₐ = b₁ * q⁽ᵃ⁻¹⁾ где q = (b₍ₐ₋₁₎) / bₐ⇒ q = 2 (по условию) ; Сумма первых пяти членов данной геометрической прогрессии..
A1 + a2 + a(2 * 2) + a(2 * 2 * 2) + a(2 * 2 * 2 * 2) = 186 A1 + a2 + a4 + a8 + a16 = 186 A = 186 : (1 + 2 + 4 + 8 + 16) A = 186 : 31 A = 6 A16 = 6 * 16 A16 = 96 Ответ : 96.
Смотри фото ∠ВОС = 80 — 36 = 44°.
1. 65 2. 67. 5 и 112. 5 3. 110 и 70 4. 120 и 60.
Рисунок построен не правильно т. К. в треугольнике с прямым углом сумма двух углов равна 220 градусов, а сумма всех углов треугольника равна 180 градусов.
Второе третий угол равен 114° второй и четвертый углы равны 66°.
Смежный угол угла в 110° будет равняться 180° — 110° = 70° В получившемся прямоугольном треугольнике известны углы 70° и 90°, значит третий угол будет равен 90° — 70° = 20° Биссектрисса, которая делилп острый угол, образовала два угла по 20°, значит ..
Если КОМ = 58, то ВОС = 58, т. К. эти углы вертикальные АОС = СОВ + ВОА = 58 + 47 = 105 Если ВОА = 47, то ДОК = 47, так как эти углы вертикальные Если сумма смежных углов равна 180, то СОД = 180 — ВОС — ДОК = 180 — 58 — 47 = 75 СОК = СОД + ДОК = 75 ..
💡 Видео
Найдите гипотенузуСкачать

Теорема Пифагора для чайников)))Скачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Нахождение стороны прямоугольного треугольникаСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ . §15 геометрия 8 классСкачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

В прямоугольном треугольнике ABC ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

В прямоугольном треугольнике гипотенуза равна 6 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

№171. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскостиСкачать
ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

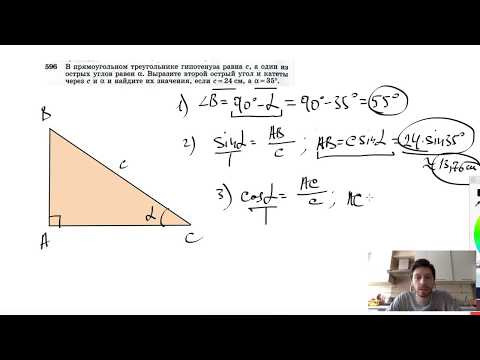
№596. В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен αСкачать