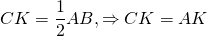Как найти угол между медианой и высотой в прямоугольном треугольнике, если известны его острые углы?
Острые углы прямоугольного треугольника равны α и β (β>α). Найти угол между медианой и высотой, проведенными из вершины прямого угла.
Дано : ∆ ABC, ∠C=90º,
Так как сумма острых углов прямоугольного треугольника равна 90º, в треугольнике ABC ∠A+∠B=90º, то есть α+β=90º. Значит, β=90º-α.
Следовательно, треугольник ACK- равнобедренный с основанием AC. Отсюда, ∠ACK=∠A=α (как углы при основании равнобедренного треугольника).
Рассмотрим треугольник ACF — прямоугольный (∠CFA=90º, так как CF — высота).
∠A+∠ACF=90º, откуда ∠ACF=90º-∠A=90º-α=β.
Вывод : угол между медианой и высотой, проведёнными к гипотенузе, равен разности острых углов прямоугольного треугольника.
Поскольку две другие высоты прямоугольного треугольника совпадают с его катетами, то угол между медианой и высотой, проведённой к катету, есть угол между медианой и другим катетом. Для нахождения этих углов требуются дополнительные данные.
∠CBP — угол между медианой BP и высотой BC
(высота BC является также катетом).
∠CAE — угол между медианой AE и высотой AC
Видео:Угол между векторами. 9 класс.Скачать
Угол между высотой и медианой вектора
Найдем координаты точки D (медианы стороны ВС):
Xd=(3+4)/2=3,5.
Yd=(1-2)/2=-0,5.
D(3,5;-0,5). Вектор AD или AD.
Модуль вектора |AD|=√(6,25+12,25)=√18,5.
Уравнение прямой ВС:
(X-Xb)/(Xc-Xb)=(Y-Yb)/(Yc-Yb) или
(X-4)/(-1)=(Y-1)/(-3) — каноническое уравнение.
Уравнение прямой ВС в общем виде Ax+By+C=0:
3х-y-11=0, где А=3, В=-1, С=-11.
Вектор нормали прямой — это перпендикуляр к прямой.
Координаты вектора нормали из уравнения прямой ВС:
n==. Этот же вектор — направляющий вектор для прямой АЕ.
Формула для уравнения прямой, проходящей через точку А(1;3)
и имеющей направляющий вектор р, то есть уравнение прямой АЕ:
(X-1)/3=(Y-3)/-1 — каноническое уравнение.
х+3y-10=0 — общее уравнение прямой АЕ.
Найдем точку пересечения прямых АЕ и ВС:
Система двух уравнений:
3х-y-11=0 и х+3y-10=0. Решаем систему и имееи:
Х=4,3 и Y=1,9/ То есть точка Е(4,3;1,9).
Тогда вектор АЕ. Модуль вектора |AE|=√(10,89+1,21)=√12,1.
Угол между векторами AD и ВЕ:
Cosα=(Xad*Xae+Yad*Yae)/(√18,5*√12,1)≈ 12,1/14,96 ≈ 0,809.
Ответ: угол между векторами равен arccos(0,809. или α≈36°.
Второй вариант:
Находим точку D(3,5;-0,5). Вектор AD.
Медиана (Модуль вектора) |AD|=√(6,25+12,25)=√18,5. (смотри первый вариант).
Находим площадь треугольника по координатам его вершин по формуле
(по формуле Герона, когда стороны — сплошные корни не хочется решать):
S=(1/2)|(Xa-Xc)*(Yb-Yc)-(Xb-Xc)(Ya-Yc)| или в нашем случае:
S=(1/2)|(1-3)*(1+2)-(4-3)(3+2)|= 5,5.
Находим длину стороны ВС:
|BC|=√[(Xc-Xb)²+(Yc-Yb)²] или BC=√[(-1)²+(-3)²] =√10.
Тогда высота треугольника АЕ=2*S/ВС= 11√10/10.
Угол между высотой АЕ и медианой AD определяем по косинусу угла Спасибо
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать
Задача. Найти угол между высотой и медианой прямоугольного треугольника
| Найдіть кут між медіаною і висотою прямокутного трикутника , які проведені з вершини прямого кута , якщо гострий кут дорівнює 20 градусів | Найдите угол между высотой и медианой прямоугольного треугольника, которые проведены из вершины прямого угла, если острый угол равен 20 градусов |
.
Решение.
Решим задачу путем дополнительного построения вокруг заданной геометрической фигуры (треугольника), чтобы использовать свойства новой образованной фигуры (прямоугольника) для решения этой задачи по геометрии
Сначала достроим прямоугольный треугольник до прямоугольника.
В результате дополнительного построения катеты прямоугольного треугольника одновременно являются сторонами прямоугольника, а гипотенуза — его диагональю.
Далее учтем следующие свойства треугольника и прямоугольника:
- Сумма углов треугольника равна 180 градусам
- Диагонали прямоугольника в точке пересечения делятся пополам
- Диагонали прямоугольника равны
Величина одного из углов треугольника задана в условии задачи. Поскольку треугольник по условию прямоугольный, то мы можем найти величину третьего угла, зная, что сумма углов треугольника равна 180 градусам.
Поскольку угол CAB = 20°, то угол ABC = 180 — 90 — 20 = 70°
Таким образом, мы нашли градусную меру угла B в треугольнике ABC
Рассмотрим треугольник COA. Он равнобедренный, так как его стороны — это половины диагоналей прямоугольника. Это следует из свойств прямоугольника. Так как диагонали прямоугольника равны, а в точке пересечения они делятся пополам, то половины равных отрезков будут также между собой равны. Поскольку в равнобедренном треугольнике углы при основании равны, то:
∠OCA = ∠OAC = 20º
Рассмотрим треугольник BKC. CK является высотой треугольника ABC, проведенной к гипотенузе. Значит угол BKC — прямой, то есть равен 90 градусам, а сам треугольник BKC — прямоугольный. Поскольку треугольник BKC — прямоугольный, то угол BCK = 180 — 90 — 70 = 20°. (Это следует из того, что сумма углов треугольника 180 градусов, угол BKC — прямой, а величину угла B мы нашли ранее)
Поскольку угол BCA — прямой, то его градусная мера равна 90 градусов и, одновременно, равна сумме градусных мер составляющих его углов: BCK, KCO и OCA.
Величину угла BCK мы только что нашли, она составляет 20 градусов, величину угла OCA мы также нашли ранее и она тоже составляет 20 градусов.
Откуда:
20° + 20° + ∠KCO = 90°
∠KCO = 50°
Ответ: Угол между медианой и биссектрисой заданного прямоугольного треугольника равен 50 градусов.
🎦 Видео
Угол между медианой и высотойСкачать
11 класс, 5 урок, Угол между векторамиСкачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
ЕГЭ база #15 / Треугольники и их элементы / Угол между биссектрисой, медианой и высотой / решу егэСкачать
Найти угол между высотой BD и медианой ВЕ этого треугольникаСкачать
Угол между векторами | МатематикаСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
100 тренировочных задач #135 Угол между векторамиСкачать
Уравнения стороны треугольника и медианыСкачать
Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать
Геометрия 9 класс (Урок№18 - Угол между векторами. Скалярное произведение векторов.)Скачать
Вычисляем высоту через координаты вершин 1Скачать
найти угол между единичными векторамиСкачать
Вычисляем угол через координаты вершинСкачать
Как находить угол между векторамиСкачать
Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать
Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
9 класс, 17 урок, Угол между векторамиСкачать
