Площадь основания треугольника призмы

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.

Формула площади правильной призмы

1. Общая формула

Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.

Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.

Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.

2. Площадь правильной треугольной призмы

Основание: равносторонний треугольник.

<table data-id="97" data-view-id="97_79105" data-title="Площадь правильной треугольной призмы" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

ПлощадьФормулаоснование

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value="» data-order=»«> боковая поверхностьполная

<td data-cell-id="B4" data-x="1" data-y="4" data-db-index="4" data-cell-type="text" data-original-value="» data-order=»«>

3. Площадь правильной четырехугольной призмы

Основание: квадрат.

<table data-id="98" data-view-id="98_52245" data-title="Площадь правильной четырехугольной призмы" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

ПлощадьФормулаоснованиебоковая поверхностьполная

Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a 2 . А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a 2 .

4. Площадь правильной шестиугольной призмы

Основание: правильный шестиугольник

<table data-id="99" data-view-id="99_96678" data-title="Площадь правильной шестиугольной призмы" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

ПлощадьФормулаоснование

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value="» data-order=»«> боковая поверхностьполная

<td data-cell-id="B4" data-x="1" data-y="4" data-db-index="4" data-cell-type="text" data-original-value="» data-order=»«>

Примеры задач

Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.

Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:

Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см 2 . Найдите ее высоту, если известно, что сторона основания равна 5 см.

Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:

Геометрические фигуры

Объём призмы

V =	n	ha 2 ctg	π
	4		n

Что такое треугольная призма?

Перед тем как приводить формулу объема треугольной призмы, рассмотрим свойства этой фигуры.

Чтобы получить этот вид призмы, необходимо взять треугольник произвольной формы и параллельно самому себе перенести его на некоторое расстояние. Вершины треугольника в начальном и конечном положении следует соединить прямыми отрезками. Полученная объемная фигура называется треугольной призмой. Она состоит из пяти сторон. Две из них называются основаниями: они параллельны и равны друг другу. Основаниями рассматриваемой призмы являются треугольники. Три оставшиеся стороны – это параллелограммы.

Помимо сторон, рассматриваемая призма характеризуется шестью вершинами (по три для каждого основания) и девятью ребрами (6 ребер лежат в плоскостях оснований и 3 ребра образованы пересечением боковых сторон). Если боковые ребра перпендикулярны основаниям, то такая призма называется прямоугольной.

Отличие треугольной призмы от всех остальных фигур этого класса заключается в том, что она всегда является выпуклой (четырех-, пяти-, …, n-угольные призмы могут также быть вогнутыми).

Правильная треугольная призма – это прямоугольная фигура, в основании которой лежит равносторонний треугольник.

Формула объема треугольной призмы правильной

Многогранник, который мы изучаем, будет правильным, если две его грани являются одинаковыми треугольниками равносторонними и три грани — это одинаковые прямоугольники. Формулу для объема такой призмы несложно получить из выражения общего вида, записанного в пункте выше. Чтобы это сделать, рассчитаем сначала площадь основания:

So = 1 / 2 × ha × a = 1 / 2 × √3 / 2 × a × a = √3 / 4 × a2

Значение высоты треугольника ha получено, исходя из того факта, что для равностороннего основания она является также медианой и биссектрисой. Таким образом, площадь So является функцией только одного параметра (стороны a).

Формулу объема для изучаемой призмы можно получить, если умножить на высоту выражение выше:

Поскольку для рассматриваемой фигуры высота равна длине бокового ребра b, то полученное выражение также можно переписать через параметры a и b.

Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы .

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы .

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

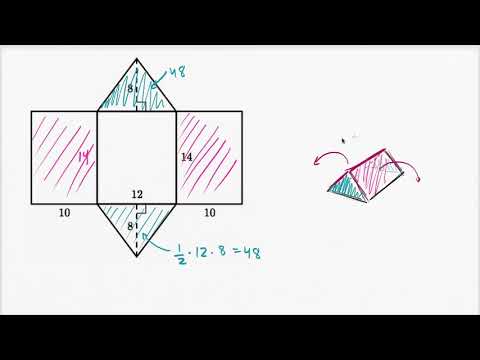
Найти объем призмы, зная площадь основания и высоту

Найти объем правильной треугольной призмы, зная ребра

Объем правильной фигуры через значение ее диагонали

Треугольная призма является самой простой фигурой из своего класса, поэтому она обладает всего одним единственным типом диагонали. Это диагонали трех ее параллелограммов.

Предположим, что имеется правильная фигура, диагональ которой равна d (это диагональ прямоугольника), а высота равна h. Как рассчитать ее объем?

Для начала следует определить значение стороны основания a. Для этого воспользуемся теоремой Пифагора:

Тогда формула объема треугольной призмы приобретает вид:

V = √3 / 4 × a2 × h = √3 / 4 × (d2 — h2) × h

В случае правильной призмы объем всегда является функцией двух параметров (h и d в данном выражении).

Виды призм

• Прямая призма – это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.

• Наклонная призма – это призма, в которой боковые грани не перпендикулярны к основанию.

• Правильная призма – это призма, в которой основания являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.

• Усечённая призма – это призма, в которой основания не параллельны друг другу. Усечённая призма может быть, как прямой, так наклонной.

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Вычисление объема правильной пятиугольной призмы

• Больше информации о том, как найти апофему, если она не дана, можно найти здесь . [5]

• А = 1/2 х 5 х сторона х апофема.
• А= 1/2 х 5 х 6 см х 7 см = 105 см 2 .

• 105 см 2 x 10 см = 1050 см 3 .

Формула вычисления объема призмы

Объем призмы равняется произведению площади ее основания на высоту.

V = S_осн ⋅ h

• S_осн – площадь основания, т.е. в нашем случае – четырехугольника ABCD или EFGH (равны между собой);
• h – высота призмы.

Приведенная выше формула подходит для следующих видов призм:

• прямой – боковые ребра перпендикулярны основанию;
• правильной – прямая призма, основанием которой является правильный многоугольник;
• наклонной – боковые ребра расположены под углом по отношению к основанию.

Необычная формула объёма призмы

Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы .

– площадь сечения, перпендикулярного боковому ребру,

– длина бокового ребра.

Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.

Давай теперь для упражнения посчитаем объём самых популярных призм.

Как рассчитывать объем фигуры произвольного типа?

Часть пространства, которая ограничена плоскими сторонами геометрической фигуры, называется ее объемом. В общем случае для призмы абсолютно любого типа справедлива следующая формула для определения ее объема:

Как видно, она очень проста и содержит всего два множителя: So — площадь одного основания, h — высота призмы, то есть дистанция между ее основаниями.

Применительно к треугольной призме произвольной формы (наклонной и неправильной), для вычисления величины So можно воспользоваться универсальной формулой для треугольника:

Здесь a — сторона треугольника, ha — высота треугольника, опущенная на сторону a.

Расчет высоты h призмы можно провести с использованием теоремы Пифагора, если знать длину бокового ребра b и двугранные углы между основанием и боковыми гранями.

Вычисление объема трапецеидальной призмы

• Например, основание1 = 8 см, основание2 = 6 см, а высота = 10 см.
• 1/2 х ( 6 + 8 ) х 10 = 1/2 х 14 см х 10 см = 70 см 2 .

• 70 см 2 x 12 см = 840 см 3 .

Основные свойства призмы

• Основание призмы – равные многоугольники
• Высота прямой призмы равна длине бокового ребра.
• Боковые ребра призмы параллельны и равны между собой.
• Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
• Боковые грани призмы – параллелограммы
• Высота наклонной призмы всегда меньше длины ребра.
• В прямой призме грани могут быть прямоугольниками или квадратами.

Объем треугольной призмы общего типа

Как найти объем треугольной призмы? Формула в общем виде аналогична таковой для призмы любого вида. Она имеет такую математическую запись:

Здесь h – это высота фигуры, то есть расстояние между ее основаниями, So – площадь треугольника.

Величину So можно найти, если известны некоторые параметры для треугольника, например одна его сторона и два угла или две стороны и один угол. Площадь треугольника равна половине произведения его высоты на длину стороны, на которую опущена эта высота.

Что касается высоты h фигуры, то ее проще всего найти для прямоугольной призмы. В последнем случае h совпадает с длиной бокового ребра.

Площадь поверхности призмы

Формула. Площадь поверхности правильной призмы через высоту ( h ), длину стороны ( a ) и количество сторон ( n ):

S =	n	a 2 ctg	π	+ nah
	2		n

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Объем прямой фигуры с прямоугольным треугольником в основании

Прямоугольный треугольник представляет собой фигуру из трех сторон, две из которых пересекаются под прямым углом. Эти стороны называются катетами. Обозначим их a1 и a2. Третья сторона называется гипотенузой (a3). Из планиметрии известно каждому школьнику, что если взять половину произведения катетов, то можно получить площадь рассматриваемого треугольника, то есть:

Так как призма является прямой, то достаточно умножить на So длину ее бокового ребра b, чтобы получить объем фигуры:

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Призма

Призма

Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.

Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.

Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Формулы вычисления объема и площади поверхности призмы:

Чтобы были понятны формулы, введем обозначения:

$P_$ — периметр основания;

$S_$ — площадь основания;

$S_$ — площадь боковой поверхности;

$S_$ — площадь полной поверхности;

$h$ — высота призмы.

В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

1. $S=/$, где $h_a$ — высота, проведенная к стороне $а$
2. $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
3. Формула Герона $S=√

   $, где $р$ — это полупериметр $p=/$

4. $S=p·r$, где $r$ — радиус вписанной окружности
5. $S=/$, где $R$ — радиус описанной окружности
6. Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.

В основании лежит четырехугольник

1. Прямоугольник

$S=a·b$, где $а$ и $b$ — смежные стороны.

2. Ромб

$S=/$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

3. Трапеция

$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.

Прямая призма называется правильной, если ее основания – правильные многоугольники.

Рассмотрим площади правильных многоугольников:

1. Для равностороннего треугольника $S=/$, где $а$ — длина стороны.

$S=a^2$, где $а$ — сторона квадрата.

3. Правильный шестиугольник

Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:

Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.

Построим прямую призму, в основании которой лежит ромб.

Распишем формулу площади полной поверхности:

В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$

Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.

Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.

Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.

Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:

Цилиндр — это та же призма, в основании которой лежит круг.

Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.

Средняя линия треугольника параллельна основанию и равна его половине.

$MN$ — средняя линия, так как соединяет середины соседних сторон.

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)

1. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
2. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: