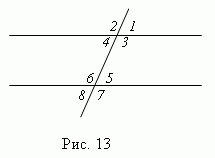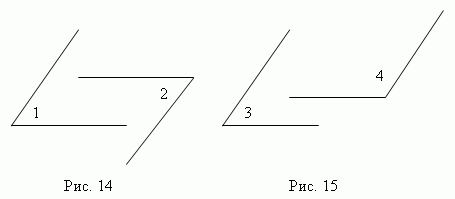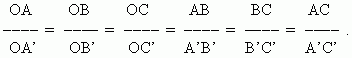Угол между параллельными прямыми равен 180 градусов верно или нет (8 видео)

Параллельность прямых

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Определение параллельности прямых
Свойства и признаки параллельных прямых
Задача 1
Задача 2
Параллельные прямые
4.3. Угол между направлениями. Параллельные прямые
📽️ Видео

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

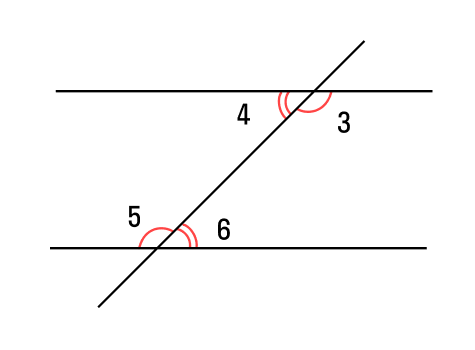
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

два внутренних накрест лежащих угла равны между собой:

два соответственных угла равны между собой:

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Видео:Пары углов в геометрииСкачать

Параллельные прямые

Параллельные прямые . Расстояние между параллельными прямыми .
Углы с соответственно параллельными сторонами .

Соответственные углы .
Внутренние и внешние накрест лежащие углы .

Внутренние и внешние односторонние углы .

Углы с соответственно перпендикулярными сторонами .
Пропорциональные отрезки . Теорема Фалеса.

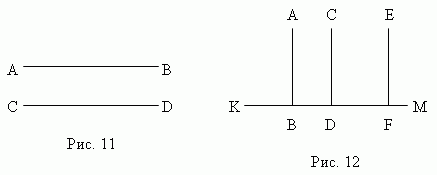
Две прямые AB и CD ( рис.11 ) называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB || CD . Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180 ° , если их направления противоположны. Все перпендикуляры ( AB , CD , EF , рис.12 ) к одной и той же прямой KM параллельны между собой. Обратно, прямая KM , перпендикулярная к одной из параллельных прямых, перпендикулярна и к остальным. Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, есть расстояние между ними.

При пересечении двух параллельных прямых третьей прямой, образуются восемь углов ( рис.13 ), которые попарно называются:

1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно

равны: ( 1 = 5; 2 = 6; 3 = 7; 4 = 8 );

2) внутренние накрест лежащие углы ( 4 и 5; 3 и 6 ); они попарно равны;

3) внешние накрест лежащие углы ( 1 и 8; 2 и 7 ); они попарно равны;

4) внутренние односторонние углы ( 3 и 5; 4 и 6 ); их сумма равна 180 °

( 3 + 5 = 180 ° ; 4 + 6 = 180 ° );

5) внешние односторонние углы ( 1 и 7; 2 и 8 ); их сумма равна 180 °

( 1 + 7 = 180 ° ; 2 + 8 = 180 ° ).

Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые, 1 = 2 , рис.14 ), либо их сумма равна 180 ° ( 3 + 4 = 180 ° , рис.15 ).

Углы с соответственно перпендикулярными сторонами также либо равны друг другу ( если они оба острые, или оба тупые ), либо их сумма равна 180 ° .

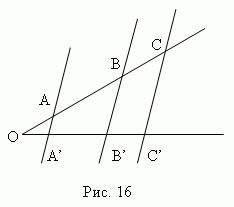
Теорема Фалеса. При пересечении сторон угла параллельными прямыми ( рис.16 ) стороны угла делятся на пропорциональные отрезки:

Видео:9. Угол между прямымиСкачать

4.3. Угол между направлениями. Параллельные прямые

Для того чтобы мы могли определить угол между двумя лучами, они вовсе необязательно должны иметь общее начало. В самом деле, каждый луч, независимо от того, где он начинается, задает какое-то направление на плоскости, а различие между двумя направлениями характеризуется не чем иным, как углом — точнее говоря, угловым расстоянием или, с учетом знака, угловым смещением.

Рассмотрим лучи OА и OВ с общим началом в точке O. Обозначим угол между ними через γ . Давайте, однако, договоримся, что здесь и далее в этих рассуждениях под «углом» мы будем понимать не угловое расстояние, а угловое смещение, которое может быть положительным или отрицательным. Об этом на рисунках нам будет напоминать стрелка у дуги, обозначающей угол:

Пусть на луче OA между O и A задана произвольная точка A₀, а на луче OB между O и B — произвольная точка B₀. Очевидно, что угол между лучами A₀A и B₀B тоже равен γ , хотя на этот раз лучи исходят не из одной точки.

Этот угол мы могли бы найти и другим способом. Проведем через точки A₀ и B₀ прямую и отметим на ней точки A₁ и B₁, как показано на рисунке:

Измерим углы ∠A₁A₀A и ∠A₁B₀B и обозначим результаты наших измерений через α и β соответственно. Эти углы (а точнее — угловые смещения) отсчитываются от одного и того же направления, задаваемого лучом B₀A₁. Очевидно, что угол γ можно вычислить как

Пусть теперь на плоскости нам даны два произвольных луча B₀B и A₀A. Опираясь на предыдущие рассуждения, мы всегда можем найти угол γ между ними одним из следующих двух способов.

Первый способ. Восстановить исходные лучи до полных прямых, найти точку их пересечения и непосредственно измерить угол γ между подходящими лучами, начинающимися в этой точке:

Второй способ. Провести прямую через точки A₀ и B₀, измерить образовавшиеся углы α и β и вычислить угол γ по формуле γ = β − α .

Необходимо отметить, что второй способ работает всегда, а с первым способом могут возникнуть проблемы. Это случается, в частности, тогда, когда углы α и β в точности равны друг другу:

В этом случае угол γ , вычисляемый по формуле γ = β − α , обращается в нуль. А это означает, что прямые, восстановленные из лучей B₀B и A₀A, нигде не пересекаются.

Действительно, если бы они пересекались, то угол γ можно было бы измерить в точке пересечения непосредственно, но тогда он оказался бы отличен от нуля.

Пусть две несовпадающие прямые принадлежат одной плоскости и на них лежат лучи, угол между которыми равен нулю. Про такие прямые говорят, что они параллельны друг другу. Важнейшее свойство параллельных прямых заключается в том, что они нигде не пересекаются.

Вернемся к задаче о нахождении угла γ между двумя произвольными лучами B₀B и A₀A с началом в разных точках. Мы только что рассмотрели особый случай, когда этот угол равен нулю. Про лучи, угловое расстояние между которыми равно нулю, говорят, что они сонаправлены или параллельны. Возможен другой особый случай, когда угол γ , рассчитанный по формуле γ = β − α , оказывается равен 180° или −180°:

Такие лучи называются противонаправленными или антипараллельными. Несложно видеть, что прямые, восстановленные из этих лучей, параллельны друг другу и, таким образом, этот случай очень похож на предыдущий.

Постороение параллельных прямых

Пусть на листе бумаги начерчена некоторая прямая n и мы хотим провести другую прямую, параллельную первой. Делается это так. Совместим с прямой n одну из сторон чертежного треугольника. К другой стороне треугольника приставим линейку. Прочно держим линейку одной рукой и передвигаем треугольник другой рукой, скользя им вдоль линейки. После этого проводим линию по той стороне треугольника, которую первоначально мы приставляли к исходной прямой n. Новая линия образует тот же угол с линейкой, что и прямая n, а значит, обе линии параллельны друг другу.

Если мы хотим, чтобы новая прямая прошла через какую-то определенную точку, то мы всегда это может сделать, остановив скольжение угольника вдоль линейки в подходящем месте.