Теорема трех параллельных прямых (3 видео)

Параллельность 3 прямых в пространстве

Вы будете перенаправлены на Автор24

В объёмном мире возможно три основных типа отношений прямых относительно друг друга:

Прямые по отношению к друг другу скрещиваются, то есть лежат в непересекающихся плоскостях и не имеют ничего общего в отличие от пересекающихся прямых. Хорошим примером будет расположение развязки на дороге, когда над одной дорогой, которая лежит на уровне земли, сверху другая. Другая иллюстрация к этому типу отношений — река и проходящая над ней железная дорога.
Две прямые являются параллельными и в этом случае они лежат в одной плоскости. Здесь в качестве иллюстрации из мира вспомним железнодорожные рельсы, идущие параллельно друг другу. Также параллельны друг другу, например, две вертикальные грани дома.
Две прямые пересекаются друг с другом и также лежат в одной плоскости. Иллюстрация из реальной жизни — это перекрёсток обычной дороги. Также одна горизонтальная, а другая вертикальная грани дома являются примером пересекающихся прямых.

Под параллельными прямыми следует понимать прямые, лежащие в одной и той же плоскости и не имеющие каких-либо точек соприкосновения друг с другом.

Рисунок 1. Типы отношений прямых в объёмном мире

В этой статье мы более подробно познакомимся с теоремой о трёх параллельных прямых в евклидовом пространстве и её доказательством.

Содержание

Теорема о параллельности 3 прямых в евклидовом пространстве
Доказательство теоремы о параллельности трех прямых в пространстве
Готовые работы на аналогичную тему
Лемма о двух параллельных прямых, использовавшаяся для доказательства теоремы о трёх параллельных прямых
Лекция по математике на тему «Параллельность трех прямых»
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Математика: теория и методика преподавания в образовательной организации
Оставьте свой комментарий
Подарочные сертификаты
Параллельные прямые в пространстве. Параллельность трех прямых
🔍 Видео

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

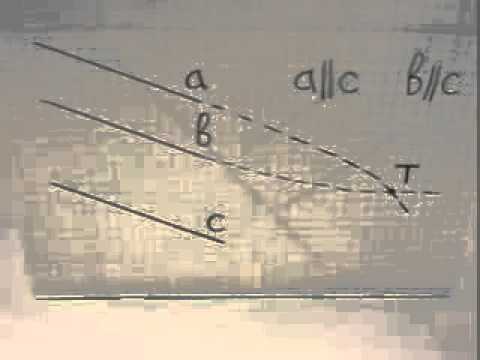
Теорема о параллельности 3 прямых в евклидовом пространстве

Если каждая из двух прямых $a$ и $b$ в пространстве параллельны некой третьей прямой $c$, то эти прямые $a$ и $b$ параллельны также между собой.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Доказательство теоремы о параллельности трех прямых в пространстве

Готовые работы на аналогичную тему

Рисунок 2. Параллельность трех прямых в пространстве — доказательство

Рассмотрим прямые $a$, $b$ и $c$, причём $a$ параллельна $c$, и $b$ параллельна $c$. Отметим на прямой $b$ точку $N$.

Как известно, прямая и не возлежащая по её длине точка достаточны для задания единственной плоскости, то есть прямая $a$ и точка $N$ являются достаточными для задания некой плоскости $α$. Теперь рассмотрим нашу вторую подопечную $b$.

Предположим, что она встречается с плоскостью $α$ в каком-то месте пространства, например, в точке $N$, тогда воспользовавшись леммой о двух параллельных прямых (см. ниже) получается, что её подруга $c$ также должна пересекать плоскость $α$.

Из этого можно сделать ошибочный вывод, что прямая $a$ тоже пересекает плоскость $α$, так как она также параллельна прямой $c$. Но это совсем не так, так как прямая $a$ возлежит в плоскости $a$.

$a$ и $b$ не имеют общих точек, так как если бы они имели их, то ситуация, при которой каждая из них при этом оставалась бы параллельна прямой $c$ была бы не реализуема, следовательно, $a$ и $b$ также параллельны друг другу.

Видео:Параллельность прямых. 10 класс.Скачать

Лемма о двух параллельных прямых, использовавшаяся для доказательства теоремы о трёх параллельных прямых

Если одна из параллельных прямых пересекает некую плоскость, то и вторая прямая также пересекает эту плоскость.

Рисунок 3. Задача о параллельности трех прямых в пространстве

Необходимо найти периметр $MNQP$, при этом $AD = 12$ см, $BC = 14$

Рисунок 4. Задача о параллельности трех прямых в пространстве

$MN || BC, QP || BC =>$ по теореме о параллельности трёх прямых $MN || QP$
$MP || DA, NQ || DA =>$ по теореме о параллельности трёх прямых $MP || NQ$
$MN || QP, MP || NQ => MNQP$ является параллелограммом
$P_ = 2 cdot (MN + MP)$
$MN = frac= frac= 7$ см
$MP = frac= frac= 6$ см
$P_ = 2 cdot (6 + 7) = 26$ см.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 01 2021

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Лекция по математике на тему «Параллельность трех прямых»

Видео:Теорема о двух прямых, параллельных третьейСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Лекция по теме «Параллельность трех прямых»

Докажем лемму о пересечении плоскости параллельными прямыми.

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает данную плоскость.

Лемма о параллельных прямых

Рассмотрим параллельные прямые а и b , одна из которых (прямая а) пересекает плоскость . Докажем, что и прямая b пересекает эту плоскость, то есть имеют одну общую точку

Доказать: b и имеют общую точку, причем она единственная

1)Пусть прямая а пересекает плоскость в точке М. Прямые а и b лежат в одной плоскости, назовем её . Плоскости и имеют общую точку М, значит, они пересекаются по прямой с .

2)Прямая с лежит в плоскости и пересекает прямую а , значит она пересекает и параллельную ей прямую b в точке Р.

3) Прямая с лежит и в плоскости альфа. Поэтому точка Р принадлежит также плоскости альфа. Если предположить, что существует ещё одна точка, принадлежащая и прямой b и плоскости альфа, то это означает, что прямая b лежит в этой плоскости и совпадает с прямой с и пересекает прямую а . А это противоречит условию. Точка Р – точка пересечения прямой b и плоскости альфа.

Что и требовалось доказать.

Эта лемма поможет доказать теорему о параллельности трёх прямых в пространстве.

Если две прямые параллельны третьей прямой, то они параллельны.

Теорема о параллельности трех прямых в пространстве

Если две прямые параллельны третьей прямой, то они параллельны.

Докажем эту теорему.

Пусть прямая а параллельна прямой с и прямая b параллельна прямой с . Докажем, что а параллельна b .

Доказательство. Для этого нужно доказать, что они лежат в одной плоскости и не пересекаются.

1) Отметим точку К на прямой b . Точка К и прямая а определяют плоскость, обозначим её .

Докажем, что прямая b лежит в этой плоскости.

2) Допустим прямая b не лежит, а пересекает эту плоскость. По лемме о параллельных прямых, прямая с, параллельная b , также пересекает эту плоскость. Но тогда и прямая а, параллельная с тоже пересекает плоскость альфа. Противоречие с условием задания плоскости. Значит прямая b лежит в плоскости. Прямые а и b не пересекаются, так как иначе через точку их пересечения проходило бы две прямые, параллельные прямой с, что противоречит теореме параллельных прямых. Теорема доказана

Необходимо доказать что а и b , и а b

1) отметим К а К и а определили плоскость , т.е. Ки а

2) (от противного)

b , b || c (по лемме о параллельных прямых) с , но тогда и а , т.к. а|| c .

Наше предположение не верно, т.е. b . И a||b ,

На рисунке точки M , N , Q и Р – середины ребер DP , DC , AC , AB . Найдите периметр четырехугольника MNQP , если AD = 12 см, BC = 14 см.

Дано: М – середина BD

А D = 12 см; ВС = 14 см

1) Рассмотрим треугольник ВС D . Отрезок MN является средней линией, значит, он параллелен ВС. Отрезок Q Р – средняя линия треугольника АВС и параллелен ВС. По теореме о параллельности трех прямых, MN параллельно Q Р.

2)МР – средняя линия треугольника D ВА, МР параллельно D А. Отрезок NQ – средняя линия треугольника АС D , NQ параллелен D А. Значит, МР параллельно NQ .

3)В четырехугольнике MNQP противоположные стороны попарно параллельны, значит, MNQP – параллелограмм.

4)Периметр параллелограмма MNQP равен удвоенной сумме смежных сторон. Длины этих сторон найдем как длины средних линий, равных половине параллельных сторон треугольника. MN равен половине ВС, 14:2 =7см, МР равен половине D А, то есть 6 см. В результате периметр равен 26 см. Задача решена.

Картинка (если на разных экранах то тетраэдр дублируется)

1) ΔВС D : MN – средняя линия, MN || ВС;

ΔАВС: Q Р – средняя линия, Q Р || ВС. Значит, MN || Q Р.

2)Δ D ВА: МР – средняя линия, МР || D А;

ΔАС D : NQ – средняя линия, NQ || D А.

3) из 1) и 2) MNQP – параллелограмм.

4) P _MNQP = 2( MN + МР);

Ответ. P _MNQP = 26см.

Треугольники АВС и ABD не лежат в одно плоскости. Докажите, что любая прямая, параллельная отрезку С D , пресекает плоскости данных треугольников

Запишем условие и построим чертеж задачи.

Так по условию точка С принадлежит плоскости АВС а точка Д принадлежит плоскости АВД, то прямая СД пересекает плоскость АВС в точке С, а плоскость АВД в точке Д.

Тогда по лемме о пересечении плоскости параллельными прямыми имеем что люба прямая параллельная АД пересекает плоскость треугольника АВС и плоскость треугольника АВД.

Дано: ΔАВС и ΔАВ D не лежат в одной плоскости

Доказать, что любая прямая, параллельная отрезку С D пересекает плоскости АВС и АВ D

Т.к. С АВС и D ABD ,

то CD ABC = C и С D ABD = D

(по лемме о пересечении плоскости параллельными прямыми)

Любая прямая || CD ABC и ABD

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 934 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 320 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 676 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Стринкевич Лилия ИльфатовнаНаписать 1100 15.12.2016

Номер материала: ДБ-025581

15.12.2016 222

15.12.2016 1293

15.12.2016 1703

15.12.2016 4890

15.12.2016 223

15.12.2016 290

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Минпросвещения создает цифровую психологическую службу для школьников

Время чтения: 1 минута

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:10 класс - Геометрия - Параллельные прямые в пространстве. Параллельность трёх прямыхСкачать

Параллельные прямые в пространстве. Параллельность трех прямых

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.