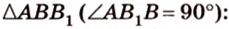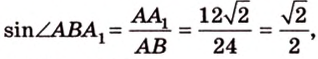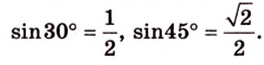- Угол между скрещивающимися прямыми и расстояние между ними. Расстояние от точки до плоскости и от прямой до параллельной ей плоскости
- Углы и расстояния в пространстве — определение и вычисление с примерами решения
- Угол между двумя прямыми в пространстве
- Угол между прямой и плоскостью в пространстве
- Угол между двумя плоскостями, пространства
- Пример №1
- Расстояния в пространстве
- Пример №2
- Пример №3
- Пример №4
- Угол между прямыми онлайн
- Предупреждение
- 1. Угол между прямыми на плоскости
- Прямые заданы каноническими уравнениями
- 1.1. Определение угла между прямыми
- 1.2. Условие параллельности прямых
- 1.3. Условие перпендикулярности прямых
- Прямые заданы общими уравнениями
- 1.4. Определение угла между прямыми
- 1.5. Условие параллельности прямых
- 1.6. Условие перпендикулярности прямых
- 2. Угол между прямыми в пространстве
- 2.1. Определение угла между прямыми
- 2.2. Условие параллельности прямых
- 2.3. Условие перпендикулярности прямых
- 💥 Видео
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Угол между скрещивающимися прямыми и расстояние между ними.
Расстояние от точки до плоскости и от прямой до параллельной ей плоскости
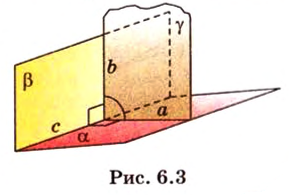
Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.
Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?
Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.
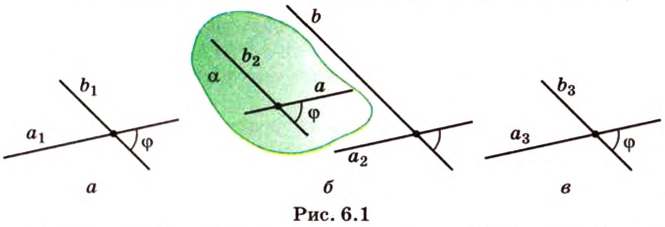
Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях ? и ?. Проведем в плоскости ? прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.
Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.
Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.
Дадим еще два полезных определения.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.
Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.
Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.
Видео:Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Углы и расстояния в пространстве — определение и вычисление с примерами решения
Содержание:
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Угол между двумя прямыми в пространстве
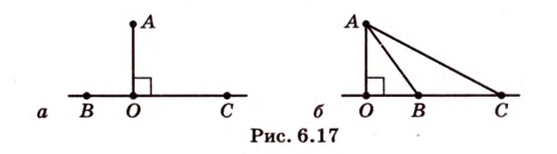
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 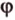
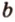
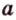
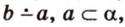
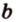
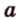
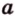
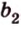
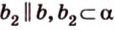
Итак,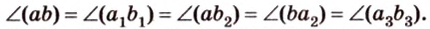
Если 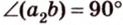
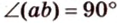
Угол между прямой и плоскостью в пространстве
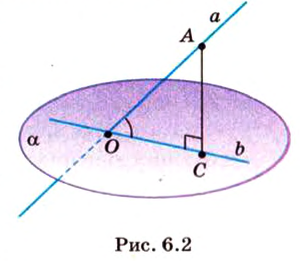
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 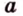
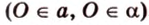
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 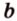
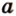
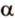
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 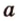
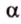
Угол между прямой 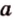
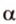
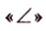
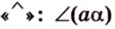
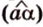
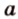
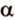
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например 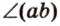
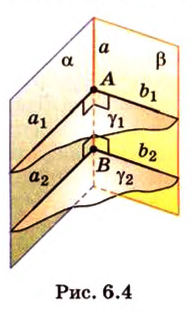
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
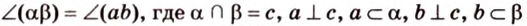
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Выберем точки 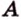
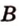
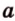
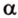
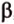
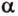
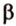
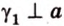
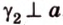
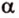
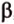
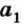
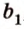
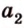
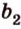
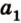
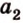
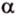
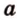
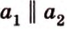
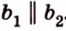
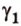
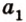
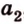
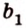
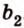
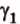
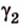
Пример №1
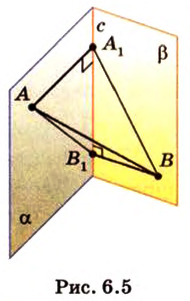
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 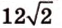
Дано: 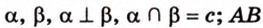
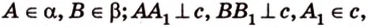
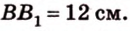
Найти: углы, образованные отрезком 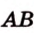
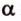
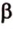
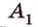
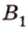
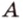
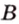
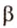
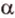
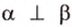
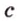
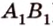
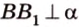
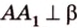
Итак, 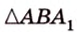
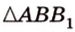
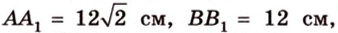
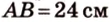
Из 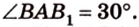
Из 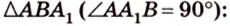
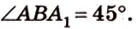
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 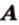
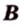
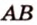
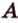
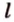
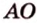
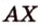
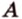
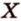
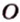
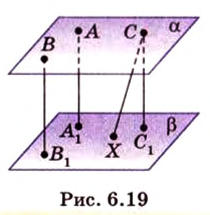
Рассмотрим плоскость 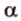
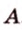
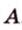
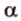
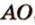
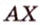
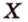
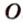
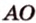
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 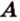
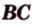
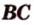
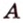
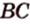
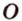
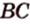
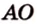
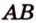

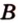
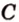
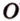
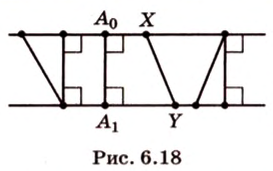
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 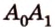
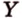
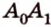
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
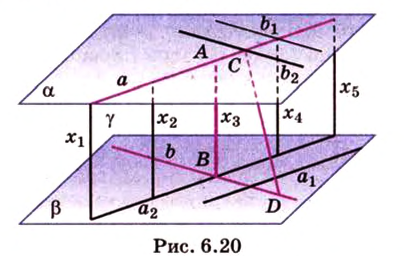
Пусть имеем две параллельные плоскости 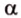
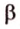
и второй, то перпендикуляр 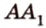
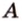
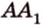
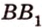
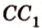
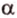
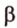
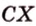
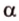
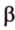
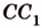
А это вытекает из того, что перпендикуляр 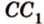
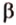
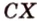
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Действительно, пусть 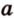
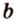
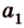
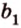
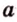
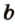
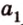
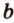
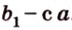
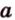
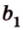
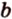
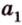
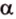
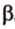
Плоскости 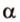
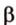
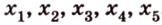
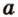
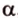
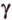
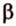
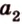
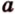
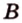
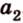
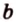
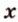
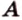
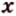
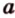
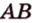
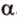
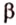
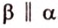
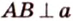
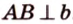
Отрезок 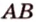
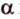
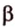
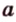
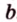
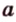
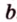
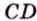
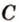
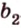
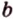

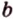
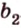
Поскольку она перпендикулярна прямым 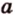
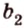

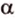




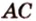
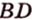
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
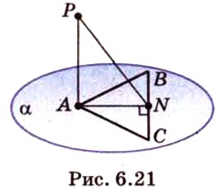
Пример №2
Отрезок 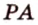
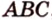
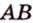
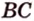
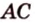
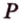
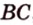
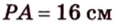
Пусть 
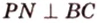
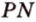
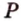
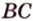
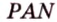
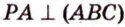
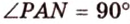
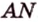
Из формулы для площади треугольника 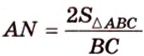
Необходимую площадь определим по формуле Герона: 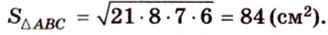
Тогда 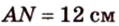
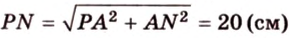
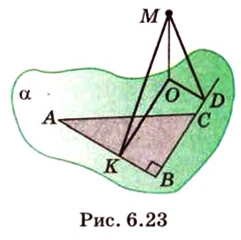
Пример №3
Прямая 
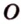
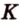
Пусть 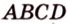
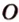
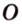
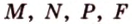
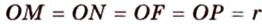
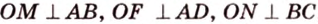
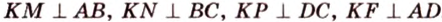
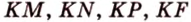
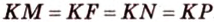
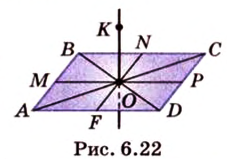
Пример №4
Точка 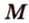
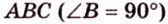
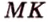
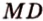
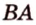
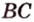
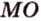
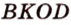
Поскольку отрезки 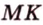
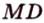
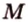
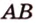
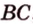
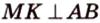
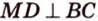
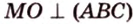
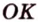
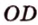
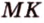
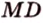
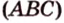
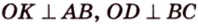
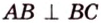
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Угол между плоскостями равен углу между прямыми, перпендикулярными к этим плоскостямСкачать

Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
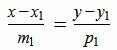 , , | (1.1) |
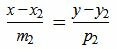 , , | (1.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
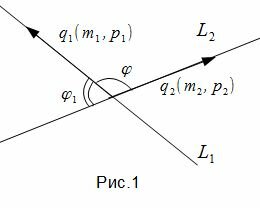 , , |
 , , | (1.3) |
Из выражения (1.3) получим:
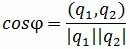 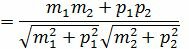 . . | (1.4) |
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
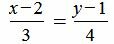 . . | (1.5) |
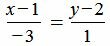 . . | (1.6) |
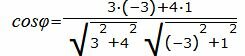 . . |
Упростим и решим:
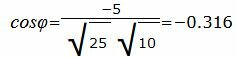 . . |
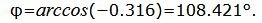 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
 |
Угол между прямыми равен:
 |
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
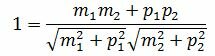 . . | (1.7) |
Сделаем преобразования с выражением (1.7):
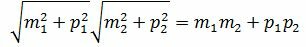 , , |
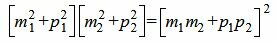 , , |
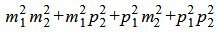 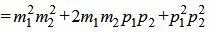 , , |
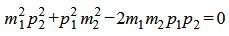 , , |
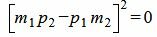 , , |
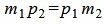 . . | (1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
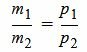 . . | (1.9) |
Пример 2. Определить, параллельны ли прямые
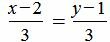 . . | (1.10) |
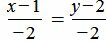 . . | (1.11) |
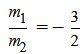 , , 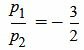 . . |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
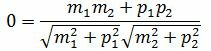 . . | (1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
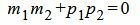 . . | (1.13) |
Пример 3. Определить, перпендикулярны ли прямые
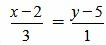 | (1.14) |
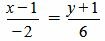 . . | (1.15) |
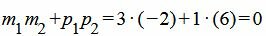 . . | (16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
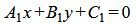 | (1.17) |
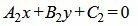 . . | (1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
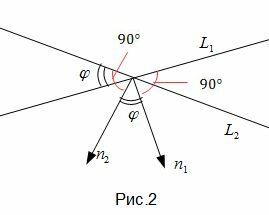 . . |
Из определения скалярного произведения двух векторов, имеем:
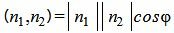 . . | (1.19) |
Из уравнения (19) получим
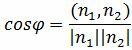 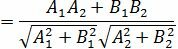 . . | (1.20) |
Пример 4. Найти угол между прямыми
| 5x1−2x2+3=0 | (1.21) |
| x1+3x2−1=0. | (1.22) |
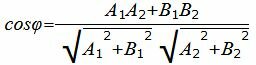 | (23) |
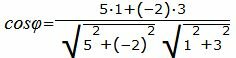 |
Упростим и решим:
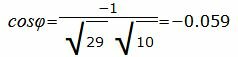 |
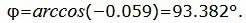 |
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
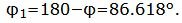 |
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
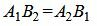 . . | (1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
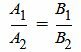 . . | (1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
| 4x+2y+2=0 | (1.26) |
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
| A1A2+B1B2=0. | (1.28) |
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
| 4x−1y+2=0 | (1.29) |
| 2x+8y−14=0. | (1.30) |
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
Видео:Угол между прямыми в пространстве. 11 класс.Скачать
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
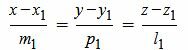 , , | (2.1) |
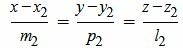 , , | (2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , | (2.3) |
Из выражения (2.3) получим:
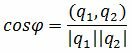 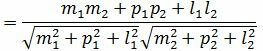 . . | (2.4) |
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
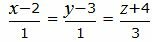 . . | (2.5) |
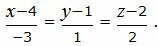 | (2.6) |
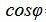 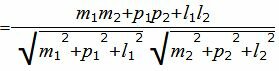 . . |
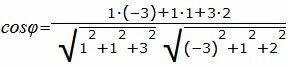 . . |
Упростим и решим:
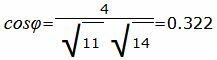 . . |
 |
Угол между прямыми равен:
 |
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
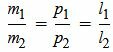 | (2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
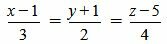 . . | (2.9) |
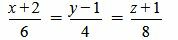 . . | (2.10) |
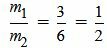 , , 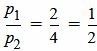 , , 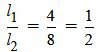 . . |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
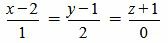 . . | (2.11) |
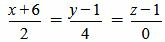 . . | (2.12) |
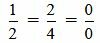 . . | (2.13) |
Выражение (2.13) нужно понимать так:
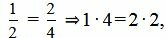 , , 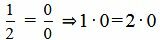 , , 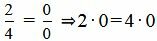 . . | (2.14) |
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
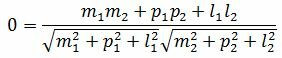 . . | (2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
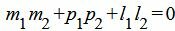 . . | (2.16) |
Пример 3. Определить, перпендикулярны ли прямые
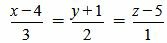 | (2.17) |
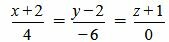 . . | (2.18) |
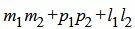 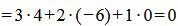 . . | (2.19) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
💥 Видео
10 класс, 9 урок, Угол между прямымиСкачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

Урок 6. Угол между прямыми в пространстве. Стереометрия с нуля.Скачать

Видеоурок "Угол между прямыми в пространстве"Скачать
Взаимное расположение прямых в пространстве. 10 класс.Скачать

Видеоурок "Угол между прямыми"Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Стереометрия для ЕГЭ: 3 - угол между прямыми и плоскостьюСкачать

ЕГЭ по математике - Угол между скрещивающимися прямымиСкачать

9. Угол между прямымиСкачать

Перпендикулярность прямой и плоскости. 10 класс.Скачать

10 класс, 21 урок, Угол между прямой и плоскостьюСкачать




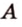 прямой
прямой 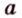
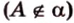 ;
;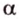
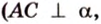
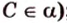 ;
;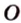 и
и  прямую
прямую 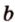 .
.