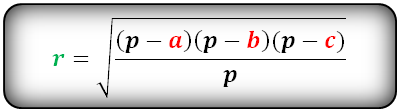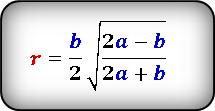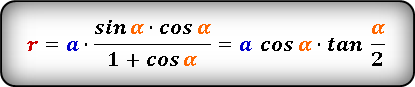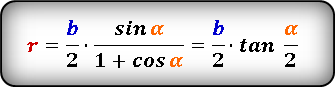Как найти сторону равнобедренного треугольника вписанного в окружность

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Равнобедренные треугольники

Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.

1. В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.

6. В равнобедренном треугольнике:

— биссектрисы, проведенные из вершин при основании, равны;

— высоты, проведенные из вершин при основании, равны;

— медианы, проведенные из вершин при основании, равны.

7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.

8. Вписанная окружность точкой касания делит основание пополам.

Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

$∠BCD$ — внешний угол треугольника $АВС$.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$.

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

1. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
2. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
3. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$cos BOA= — cos BOC;$

$ctg BOA= — ctg BOC.$

В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.

Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)

Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$

Рассмотрим прямоугольный треугольник $АНС$.

Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:

Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:

Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

В треугольнике $АВС$ $ВС=16, sin∠A=/$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.

Воспользуемся теоремой синусов:

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности

Далее подставим числовые данные и найдем $R$

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Видео:№690. Найдите основание равнобедренного треугольника, если центр вписанной в него окружностиСкачать

Все формулы для радиуса вписанной окружности

Видео:№250. Найдите сторону равнобедренного треугольника, если две другие стороны равны: а) 7 см и 3 смСкачать

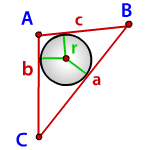
Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

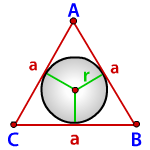
Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

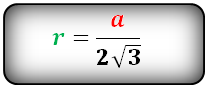
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Видео:Известна биссектриса равностороннего треугольника. Найти сторону этого треугольника. ОГЭ №16Скачать

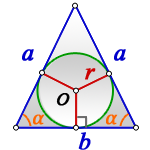
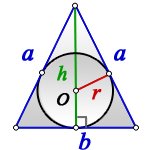
Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

💡 Видео

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

ЕГЭ 6 номер. Нахождение стороны правильного треугольника по радиусу вписанной окружности.Скачать

№689. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 смСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

№490. Найдите боковую сторону и площадь равнобедренного треугольника, если: а) основание равноСкачать

Вписанная окружность в равностороннем треугольникеСкачать

Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Как найти сторону равностороннего треугольника #shorts | ЕГЭ 2022 по профильной математике | ЭйджейСкачать