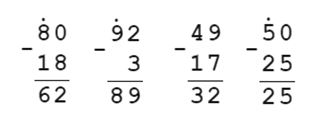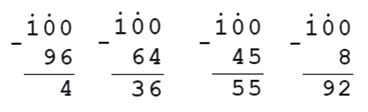Три окружности с центрами O1, O2 и O3 радиусами 1, 2 и 6 соответственно попарно касаются внешним образом. Найдите угол O1O2O3.
Решение: 
O1O2=3
O2O3=8
O1O3=7
По теореме косинусов:
O1O3 2 =O1O3 2 +O2O3 2 -2O1O2∙O2O3∙cos(O1O2O3)
7 2 =8 2 +3 2 -2∙8∙3∙cos(O1O2O3)
49=64+9-48∙cos(O1O2O3)
48∙cos(O1O2O3)=64+9-49
48∙cos(O1O2O3)=24
cos(O1O2O3)=0,5
∟O1O2O3=60°
Видео урока, где рассмотрено решение этой задачи и не только.
Кликните СЮДА, чтобы посмотреть видео.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

Окружность. Относительное взаимоположение окружностей.
Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
Видео:Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать
ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 1 Страница 87-92
| 05.10.2021, 14:56 |
Страница 87
1. Какие предметы, изображённые на рисунке, в действительности похожи на окружность, а какие — на круг?
Ответ:
На окружность похожи: 1 рисунок (тигр, который прыгает через кольцо) и 3 рисунок (обруч).
На круг похожи: 2 рисунок (леденец) и 4 рисунок (солнце).
2. Используя циркуль, начерти три разные окружности. Перед выполнением задания обдумай план его выполнения. Обязательно ли надо отмечать три разных центра окружностей?
Ответ:
Необязательно отмечать три разных центра окружностей, можно провести три окружности из одного центра.
1. Нужно отметить центр окружности — точку O.
2. Выбрать любую точку A.
3. Одну ножку циркуля поставить в центр окружности, а вторую ножку, которой будете чертить, установить в точке A и начертить окружность.
Для второй и третьей окружности нужно сделать те же самые действия, кроме первого пункта.
3. Начерти окружность и проведи три её радиуса. Сколько радиусов можно провести в одной окружности?
Ответ:
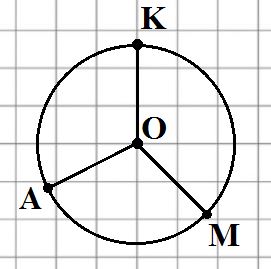
В одной окружности можно провести бесконечное множество радиусов.
Страница 88
4. Начерти с помощью циркуля окружность с центром в точке О и радиусом длиной 5 см.
Ответ:
Нужно отметить центр окружности — точку O.
Провести отрезок OA, который равен радиусу.
Одну ножку циркуля поставить в центр окружности, а вторую ножку, которой будете чертить, установить в точке A и начертить окружность. 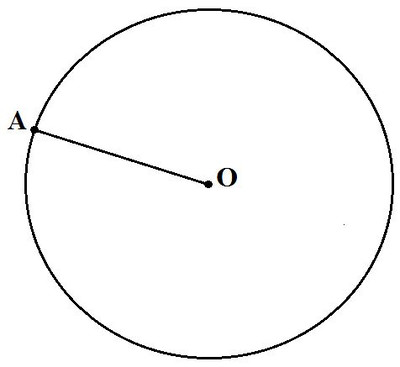
OA = 5 см
5. Начерти окружность с радиусом длиной 2 см. Начерти другую окружность с тем же центром и радиусом длиной 4 см.
Ответ: 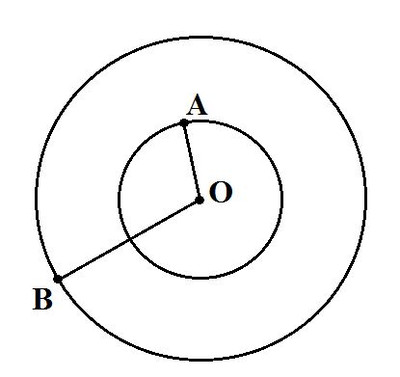
OA = 2 см
OB = 4 см
6. Сравни окружность и круг. В чём их сходство и различие?
Ответ:
Различие: Окружность — это замкнутая линия. А круг — это фигура, которая ограничена окружностью.
Сходства: Круг и окружность имеют радиус и диаметр.
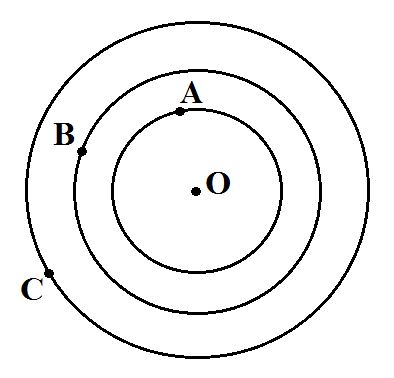
7. Начерти две разные окружности, имеющие один и тот же радиус.
Ответ: 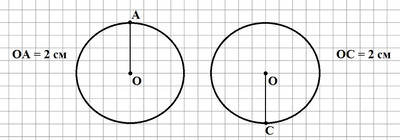
Две разные окружности OA и OC имеют один и тот же радиус, который равен 2 см.
8. Сколько окружностей ты видишь на каждом рисунке? Выбери правильный ответ.
Ответ:
На первом рисунке 6 окружностей, а на втором — 10 окружностей.
Страница 89
9. Вычисли.
(80 — 7) + 13
52 — (6 + 18)
(60 + 8) — 19
40 — (21 — 7)
Ответ:
10. Называйте по очереди ответы примеров. Если необходимо, исправляйте ошибки друг друга.
4 + 5 19 — 6 30 — 20 50 + 0
9 — 6 8 + 8 30 + 20 48 — 0
7 + 7 9 + 9 60 — 60 10 + 10
7 — 7 0 — 0 60 + 30 48 — 48
Ответ:
4 + 5 = 9
9 — 6 = 3
7 + 7 = 14
7 — 7 = 0
19 — 6 = 13
8 + 8 = 16
9 + 9 = 18
0 — 0 = 0
30 — 20 = 10
30 + 20 = 50
60 — 60 = 0
60 + 30 = 90
50 + 0 = 50
48 — 0 = 48
10 + 10 = 20
48 — 48 = 0
11. Вычисли периметр треугольника, длины сторон которого равны 2 дм 6 см, 5 дм, 3 дм 8 см.
Ответ:
Чтобы проще было считать, можно длины перевести в одинаковые единицы измерения:
2 дм 6 см = 26 см
5 дм = 50 см
3 дм 8 см = 38 см
26 см + 50 см + 38 см = 114 см = 11 дм 4 см
12. Какие из утверждений неверны?
Это не многоугольник.
Это луч АВ.
Это не кривая линия.
Это не луч.
Это отрезок.
Ответ:
Это луч AB
13. Собираясь домой, гости надели 4 пальто и 7 плащей, после чего вешалка опустела. Сколько гостей ушли домой?
Ответ:
4 + 7 = 11 вещей — надели гости, т.е. 11 гостей ушли домой
14. На двух полках стояло по 15 книг. С одной полки взяли несколько книг, а с другой взяли столько книг, сколько осталось на первой полке. Сколько всего взяли книг?
Ответ:
Допустим, что с первой полки взяли 6 книг, а со второй полки взяли столько книг, сколько осталось на первой полке.
На первой полке осталось 15 — 6 = 9 книг, значит со второй полки взяли 9 книг.
6 + 9 = 15 книг — взяли всего
Страница 90
15. В магазине продают печенье, шоколад, конфеты, вафли.
У Антона 90 рублей. Может ли он купить:
2 плитки шоколада;
пачку печенья и шоколадку;
пачку вафель, пачку печенья и плитку шоколада;
коробку конфет;
3 пачки печенья;
2 пачки вафель, шоколадку и пачку печенья?
Ответ:
2 плитки шоколада стоят: 38 + 38 = 76 рублей
90 рублей > 76 рублей, значит Антон сможет купить 2 плитки шоколада.
Пачка печенья и шоколадка стоят: 12 + 38 = 50 рублей
90 рублей > 50 рублей, значит Антон сможет купить пачку печенья и шоколадку.
Пачка вафель, пачка печенья и плитка шоколада стоят: 30 + (12 + 38) = 30 + 50 = 80 рублей
90 рублей >> 80 рублей, значит Антон сможет купить пачку вафель, пачку печенья и плитку шоколада.
Коробка конфет стоит 96 рублей
90 рублей 36 рублей, значит Антон сможет купить 3 пачки печенья.
2 пачки вафель, шоколадка и пачка печенья стоят: (30 + 30) + (38 + 12) = 60 + 50 = 110 рублей
90 рублей □ + □ ) + □ = 39.
Ответ:
1) Сначала узнаем сколько пирожков было с мясом и капустой:
12 + 15 = 27 пирожков
2) Затем узнаем сколько пирожков было с рисом:
39 — 27 = 12 пирожков
Проверка решения: (12 + 15) + 12 = 39
21. Выполни действия, записывая числа столбиком.
68 + 24 52 + 9 64 — 17 50 — 16
42 + 58 64 + 7 85 — 58 70 — 43
73 + 16 8 + 92 51 — 44 90 — 8
19 + 27 4 + 49 77 — 69 63 — 4
Ответ:
22. В некоторых числах одна из цифр в записи заменена звёздочкой. В тех случаях, где возможно, сравни пары чисел.
3 ∗ и 51 99 и ∗ 7 7 ∗ и ∗ 8
∗ 5 и ∗ 4 6 ∗ и 8 ∗ 8 ∗ и 9 ∗
Поясни свой ответ.
Ответ:
3 ∗ и 51 — 3 десятка меньше, чем 5 десятков, поэтому какая бы цифра (от 0 до 9) вместо ∗ не стояла, число 3 ∗ всегда будет меньше 51. Так что 3 ∗ ∗ 5 и ∗ 4 — в обоих случаях ∗ стоит на месте разряда десятков, поэтому пары нельзя сравнить
99 и ∗ 7 — 99 самое большое двузначное число, поэтому оно больше любого другого двузначного числа. Так что 99 > ∗ 7
6 ∗ и 8 ∗ — 6 десятков меньше, чем 8 десятков, поэтому какая бы цифра (от 0 до 9) вместо ∗ не стояла, число 6 ∗ всегда будет меньше 8 ∗ . Так что 6 ∗ 8 ∗
7 ∗ и ∗ 8 — в первом числе 7 десятков, во втором числе на месте разряда десятков стоит ∗ , вместо которой может стоять цифра больше 7, равно 7 или меньше 7, поэтому пары нельзя сравнить
8 ∗ и 9 ∗ — 8 десятков меньше, чем 9 десятков, поэтому какая бы цифра (от 0 до 9) вместо ∗ не стояла, число 8 ∗ всегда будет меньше 9 ∗ . Так что 8 ∗ 9 ∗
23. Объясни, как составлены ряды чисел. Назови ещё по три следующих числа.
1, 6, 11, 16 . .
20, 17, 14, 11 .
1, 2, 3, 5, 8 . .
Ответ:
В первом ряду каждое следующее число больше предыдущего на 5: 1, 6, 11, 16, 21, 26, 31
Во второму ряду каждое следующее число меньше предыдущего на 3: 20, 17, 14, 11, 8, 5, 2
В третьем ряду следующее число равно сумме двух предыдущих чисел: 1, 2, 3, 5, 8, 13, 21, 34
Страница 92
24. Уменьши: 80 на 18, 92 на 3, 49 на 17, 50 на 25.
Ответ:
25. Выясни, каков твой рост и рост твоего соседа по парте. Вычисли, на сколько сантиметров один из вас выше другого.
Ответ:
Например: рост первого ученика равен 130 см, а рост второго ученика равен 137 см.
137 — 130 = 7 см — второй ученик выше, чем первый
26. Сравни следующие примеры между собой. Чем они похожи и чем различаются?
100 — 45 100 — 8
100 — 64 100 — 96
Не выполняя вычислений, перепиши эти примеры в порядке увеличения их ответов.
Проверь себя: выполни вычисления.
Ответ:
У всех примеров одинаковое уменьшаемое (число 100).
Чем больше число вычитаем из уменьшаемого, тем меньше будет значение разности.
Поэтому примеры в порядке увеличения их ответов будут выглядеть так: 100 — 96; 100 — 64; 100 — 45; 100 — 8
27. Какое слово надо вставить, чтобы получилось верное утверждение? Выбери.
Канюк — это . .
1) растение 2) лодка 3) птица 4) рыба
Для ответа на вопрос можно воспользоваться толковым словарём русского языка.
Ответ:
Канюк — это хищная птица, обитающая в Старом Свете.
📽️ Видео
Г: Три равные окружности с центрами О1, О2, О3 и радиусом R попарно касаются друг друга в точках А ВСкачать

Две окружности с центрами О1 и О3 и радиусами 7 и 6 касаютсяСкачать

ОГЭ по математике. Окружности с центрами.. Вариант 3 (25)Скачать

САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Задача по темам: окружность, равнобедренный треугольник. "Окружности с центрами в точках Р и Q ..."Скачать

Как искать точки на тригонометрической окружности.Скачать

Три точки, задающие окружностьСкачать
№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

ОГЭ по математике. Окружности с центрами в точках √25 вариант 2Скачать

ОГЭ Задание 25 Две окружностиСкачать

Построение окружности по трём точкам.Скачать

Три окружностиСкачать

#23. IMO-2008, Problem 1Скачать
Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

ЕГЭ Задание 16 Три окружностиСкачать
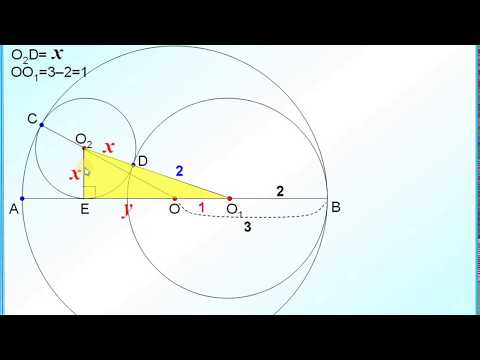
№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать