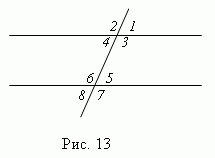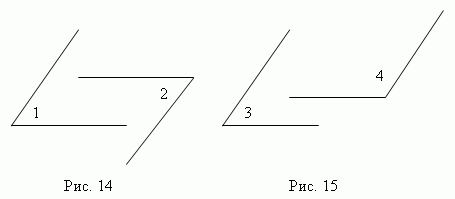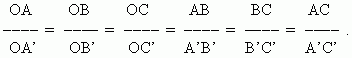Параллельные прямые . Расстояние между параллельными прямыми .
Углы с соответственно параллельными сторонами .
Соответственные углы .
Внутренние и внешние накрест лежащие углы .
Внутренние и внешние односторонние углы .
Углы с соответственно перпендикулярными сторонами .
Пропорциональные отрезки . Теорема Фалеса.
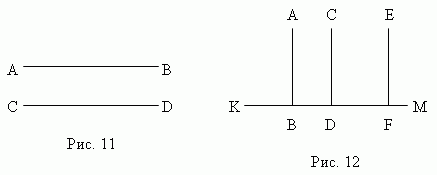
Две прямые AB и CD ( рис.11 ) называются параллельными , если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Обозначение: AB || CD . Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой. Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Угол между двумя параллельными лучами равен нулю, если у них одинаковые направления, и 180 ° , если их направления противоположны. Все перпендикуляры ( AB , CD , EF , рис.12 ) к одной и той же прямой KM параллельны между собой. Обратно, прямая KM , перпендикулярная к одной из параллельных прямых, перпендикулярна и к остальным. Длина отрезка перпендикуляра, заключённого между двумя параллельными прямыми, есть расстояние между ними.
При пересечении двух параллельных прямых третьей прямой, образуются восемь углов ( рис.13 ), которые попарно называются:
1) соответственные углы ( 1 и 5; 2 и 6; 3 и 7; 4 и 8 ); эти углы попарно
равны: (







2) внутренние накрест лежащие углы ( 4 и 5; 3 и 6 ); они попарно равны;
3) внешние накрест лежащие углы ( 1 и 8; 2 и 7 ); они попарно равны;
4) внутренние односторонние углы ( 3 и 5; 4 и 6 ); их сумма равна 180 °
( 



5) внешние односторонние углы ( 1 и 7; 2 и 8 ); их сумма равна 180 °
( 



Углы с соответственно параллельными сторонами либо равны друг другу ( если они оба острые, или оба тупые, 



Углы с соответственно перпендикулярными сторонами также либо равны друг другу ( если они оба острые, или оба тупые ), либо их сумма равна 180 ° .
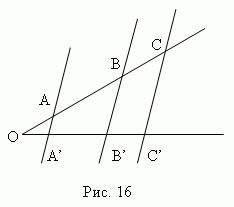
Теорема Фалеса. При пересечении сторон угла параллельными прямыми ( рис.16 ) стороны угла делятся на пропорциональные отрезки:
Copyright © 2004 — 2007 Др. Юрий Беренгард. All rights reserved.
Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Параллельность прямых
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
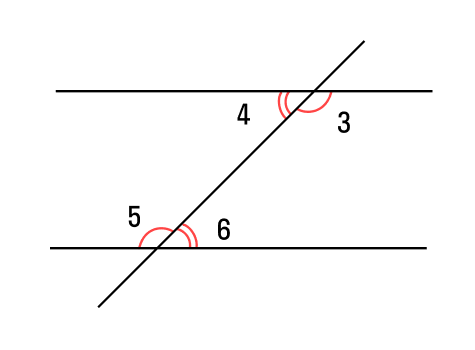
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
два внутренних накрест лежащих угла равны между собой:
два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Углы между прямыми и плоскостями
Взаимное расположение прямых и плоскостей в пространстве
Параллельность прямых и плоскостей
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Прямая и плоскость называются параллельными, если они не пересекаются.
Две плоскости называются параллельными, если они не пересекаются.
Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.
Признак параллельности прямой и плоскости. Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Признак скрещивающихся прямых. Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые скрещиваются.
Теоремыо параллельных прямых и параллельных плоскостях.
1. Две прямые, параллельные третьей прямой, параллельны.
2. Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
3. Через точку вне данной прямой можно провести прямую, параллельную данной, и только одну.
4. Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна их линии пересечения.
5. Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения параллельны.
6. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и только одну.
7. Две плоскости, параллельные третьей, параллельны между собой.
8. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Углы между прямыми и плоскостями
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость (угол 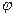
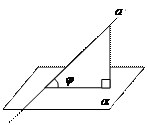 |
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, параллельными соответственно данным скрещивающимся прямым.
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей прямой. Полуплоскости называются гранями, прямая – ребром двугранного угла.
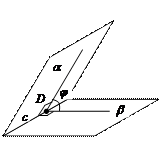
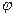
Градусная (радианная) мера двугранного угла равна градусной (радианной) мере его линейного угла.
🎥 Видео
Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Углы, образованные параллельными прямыми и секущейСкачать

29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать

Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Пары углов в геометрииСкачать

Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельные прямые (задачи).Скачать

Теоремы об углах, образованных двумя параллельными прямыми и секущей.Скачать

№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Углы при параллельных и секущей #математика #огэматематика #огэ #данирСкачать

УГЛЫ ПРИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ И СЕКУЩЕЙСкачать

10 класс, 8 урок, Углы с сонаправленными сторонамиСкачать