Доказать что середины равных хорд лежат на одной окружности (6 видео)

Докажите, что середины равных хорд окружности расположены на окружности с тем же центром.

Содержание

Ваш ответ
Похожие вопросы
Равные хорды
Хорды и дуги
Свойство дуг, заключенных между параллельными хордами
Свойство дуг, заключённых между касательной и параллельной ей хордой
Диаметр, перпендикулярный к хорде
🔍 Видео

Видео:Доказать, что точки лежат на одной окружностиСкачать

Ваш ответ

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Равные хорды

Выясним, какими свойствами обладают равные хорды и равные дуги.

Равные хорды равноудалены от центра окружности.

Дано : окр. (O;R), AB и CD — хорды,

Соединим центр окружности с концами хорд.

I. Рассмотрим треугольники AOB и COD.

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.

II. Рассмотрим прямоугольные треугольники AOF и COK.

2) ∠A=∠C (по доказанному).

Из равенства треугольников следует равенство соответствующих сторон: OF=OK.

Что и требовалось доказать .

Если хорды равноудалены от центра окружности, то они равны.

Дано: окр. (O;R), AB и CD — хорды,

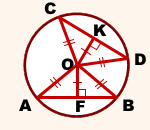
Соединим центр окружности с концами хорд.

I. Рассмотрим прямоугольные треугольники OKD и OFB.

1)OF=OK (по условию)

2)OD=OB (как радиусы).

Из равенства треугольников следует равенство соответствующих сторон:

II. Рассмотрим треугольники AOB и COD.

Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.

По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.

Что и требовалось доказать.

Равные хорды стягивают равные дуги.

Дано : окр. (O;R), AB и CD — хорды, AB=CD,

Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

1) AB=CD (по условию)

2) OA=OB=OC=OD (как радиусы).

Следовательно, ∆AOB = ∆COD (по трём сторонам).

Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.

Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD

Что и требовалось доказать .

Хорды, стягивающие равны дуги, равны.

Дано: окр. (O;R), AB и CD — хорды,

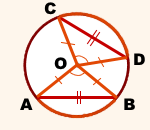
Соединим центр окружности с концами хорд.

Рассмотрим треугольники AOB и COD

Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.

Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.

Из равенства треугольников следует равенство соответствующих сторон: AB=CD.

Видео:Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Хорды и дуги

Докажем ряд теорем, устанавливающих зависимость между хордами и их дугами в одной и той же окружности или в равных окружностях.

При этом будем иметь в виду дуги, меньшие полуокружности.

Теорема 1. Равные дуги стягиваются равными хордами.

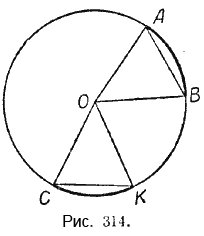
Пусть дуга АВ равна дуге СК. Требуется доказать, что и хорда АВ равна хорде СК (рис. 314).

Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны, так как имеют по две соответственно равные стороны (радиусы одной окружности) и по равному углу, заключённому между этими сторонами (эти углы равны, как центральные, соответствующие равным дугам). Следовательно, АВ = СК.

Теорема 2 (обратная). Равные хорды стягивают равные дуги.

Пусть хорда АВ равна хорде СК. Требуется доказать, что дуга АВ равна дуге СК (рис. 314).

Доказательство. Соединим концы хорд с центром окружности — точкой О. Полученные треугольники АОВ и КОС равны по трём соответственно равным сторонам. Следовательно, равны углы АОВ и СОК; но углы эти центральные, соответствующие дугам АВ и СК; из равенства этих углов следует равенство дуг: (breve = breve).

Теорема 3. Большая дуга стягивается и большей хордой.

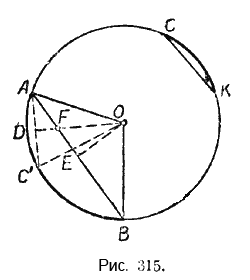
Пусть дуга АВ больше дуги СК (рис. 315).

Требуется доказать, что хорда АВ больше хорды СК.

Доказательство. Передвинем по окружности дугу СК так, чтобы точка К совместилась с точкой А, тогда точка С займёт положение С’ на дуге АВ между точками Aи В, дуга СК примет положение дуги АС’, а хорда СК примет положение хорды АС’. Проведём радиусы в точки A, В и С’. Опустим из центра О перпендикуляры ОЕ и ОD на хорды АВ и АС’. В треугольнике ОFE отрезок ОЕ — катет, а отрезок ОF — гипотенуза, поэтому OF > ОЕ, а потому и OD > OE.

Рассмотрим теперь треугольники ОАD и ОАЕ. В этих треугольниках гипотенуза ОА общая, а катет ОЕ меньше катета ОD, тогда по следствию из теоремы Пифагора катет АЕ больше катета АD. Но эти катеты составляют половины хорд АВ и АС’, значит, и хорда АВ больше хорды АС’. Вследствие равенства хорд АС’ и СК получаем
АВ > СК.

Теорема 4 (обратная). Большая хорда стягивает и большую дугу.

Пусть хорда А В больше хорды СК.

Требуется доказать, что дуга АВ больше дуги СК (рис. 315). Между дугами АВ и СК может существовать только одно из трёх следующих соотношений:

Но дуга AВ не может быть меньше дуги СК, так как тогда по прямой теореме хорда АВ была бы меньше хорды СК, а это противоречит условию теоремы.

Дуга АВ не может быть равна дуге СК, так как тогда хорда АВ равнялась бы хорде СК, а это тоже противоречит условию. Следовательно, (breve > breve).

Свойство дуг, заключенных между параллельными хордами

Теорема. Дуги, заключённые между параллельными хордами, равны.

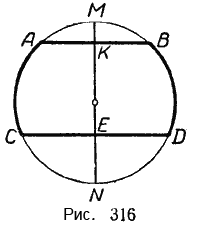
Пусть хорда AB параллельна хорде СD (рис. 316).

Требуется доказать, что (breve = breve). Проведём диаметр MN ⊥ AB. Так как CD || AB, то MN ⊥ CD.
Перегнём чертёж по диаметру MN так, чтобы правая часть совпала с левой.

Тогда точка В совпадёт с точкой А, так как они симметричны относительно оси MN (AB ⊥ MN по построению и AK = KB).

Аналогично, точка D совпадёт с точкой С. Отсюда (breve = breve).

Свойство дуг, заключённых между касательной и параллельной ей хордой

Теорема. Дуги, заключённые между касательной и параллельной ей хордой, равны.

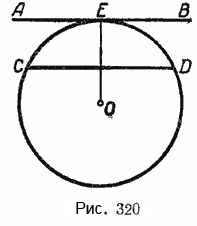
Пусть касательная АВ и хорда СD параллельны. Точка Е — точка касания прямой АВ с окружностью О (рис. 320).

Требуется доказать, что (breve = breve).

Для доказательства соединим точку касания Е с центром круга.

OE ⊥ AB, а так как СD || АВ, то OE ⊥ CD, а перпендикуляр к хорде, проведённый из центра той же окружности, делит стягиваемую ею дугу пополам.

Следовательно, (breve = breve).

Видео:✓ Степень точки в ЕГЭ | Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень | Борис ТрушинСкачать

Диаметр, перпендикулярный к хорде

Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.

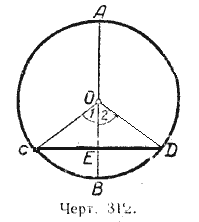
Пусть диаметр AB перпендикулярен к хорде CD (черт. 312). Требуется доказать, что
$$ CE = ED, breve = breve, breve = breve $$

Соединим точки С и D с центром окружности О. В равнобедренном треугольнике СОD отрезок ЕО является высотой, проведённой из вершины О на основание CD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и ∠1 = ∠2. Но ∠1 и ∠2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
$$ breve = breve $$
Дуги CA и ВА также равны между собой, как дополняющие равные дуги до полуокружности.

Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.

Пусть диаметр AB делит хорду CD пополам. Требуется доказать, что AB ⊥ CD,

Соединим точки С и В с центром круга. Получим равнобедренный треугольник СОD, в котором ОК является медианой, а значит, и высотой. Следовательно, AB⊥CD, а отсюда (по теореме 1) следует, что
$$ breve = breve; breve = breve $$

Теорема 3 (обратная). Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.

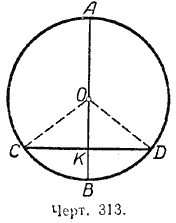
Пусть диаметр AB делит дугу СВD пополам (черт. 313). Требуется доказать, что

Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы (breve) = (breve), поэтому ОК будет и медианой и высотой этого треугольника. Следовательно, диаметр AB проходит через середину хорды и перпендикулярен к ней.