Убедиться что на векторах ab ad aa1 можно построить параллелепипед

вариантов текущего контроля

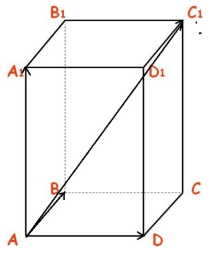
1. Домашнее задание №1. «Векторная алгебра и аналитическая геометрия»

Дано: точки , , , ; числа , ; угол .

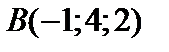
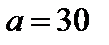
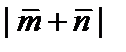
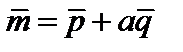
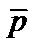
1. Найти длину вектора , если , и , — единичные векторы, угол между которыми равен .

2. Найти координаты точки М, делящей вектор в отношении .

3. Проверить, можно ли на векторах и построить параллелограмм. Если да, то найти длины сторон параллелограмма.

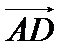
4. Найти углы между диагоналями параллелограмма ABCD.

5. Найти площадь параллелограмма ABCD.

6. Убедиться, что на векторах , , можно построить параллелепипед. Найти объем этого параллелепипеда и длину его высоты.

7. Найти координаты вектора , направленного по высоте параллелепипеда , проведенной из точки A к плоскости основания , координаты точки H и координаты единичного вектора, совпадающего по направлению с вектором .

8. Найти разложение вектора по векторам , , .

9. Найти проекцию вектора на вектор .

10. Написать уравнения плоскостей:

а) P, проходящей через точки A, B, D;

б) P₁, проходящей через точку A и прямую A₁B₁;

в) P₂, проходящей через точку A₁ параллельно плоскости P;

г) P₃ , содержащей прямые AD и AA₁;

д) P₄ , проходящей через точки A и C₁ , перпендикулярно плоскости P.

11. Найти расстояние между прямыми, на которых лежат ребра AB и CC₁; написать канонические и параметрические уравнения общего к ним перпендикуляра.

12. Найти точку A₂ , симметричную точке A₁ относительно плоскости основания ABCD.

13. Найти угол между прямой, на которой лежит диагональ A₁C, и плоскостью основания ABCD.

14. Найти острый угол между плоскостями ABC₁D (плоскость P) и ABB₁A₁ (плоскость P₁).

2. Домашнее задание №2. «Кривые и поверхности второго порядка»

В задачах 1–2 заданное уравнение линии второго порядка привести к каноническому виду и построить кривую в системе координат OXY.

В задаче 3 по приведенным данным найти уравнение кривой в системе координат OXY.

Для задач 1–3 указать:

1) канонический вид уравнения линии;

2) преобразование параллельного переноса, приводящее к каноническому виду;

3) в случае эллипса: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов; в случае гиперболы: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов, уравнения асимптот; в случае параболы: параметр, вершину, фокус, уравнение директрисы, расстояния от точки C до фокуса и директрисы;

4) для точки C проверить свойство, характеризующее данный тип кривых как геометрическое место точек.

В задаче 4 указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат OXYZ.

1) , ; 2) , .

3) Парабола симметрична относительно прямой , имеет фокус , пересекает ось OX в точке , а ее ветви лежат в полуплоскости .

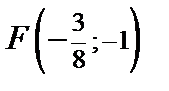
4) .

Контроль по модулю №1 “Векторная алгебра. Аналитическая геометрия”

1. Правые и левые тройки векторов. Определение векторного произведения векторов. Сформулировать свойства векторного произведения векторов. Вывести формулу вычисления векторного произведения двух векторов, заданных своими координатами в ортонормированном базисе.

2. Найти угол между векторами если

3. Найти, если это возможно, разложение вектора по векторам и

4. Составить уравнение плоскости, проходящей через точки , и перпендикулярной плоскости Составить канонические уравнения прямой, проходящей через точку и ортогональной к найденной плоскости.

Последнее изменение этой страницы: 2016-12-09; Нарушение авторского права страницы

По координатам точек считаешь векторы.

Вектор от точки C (x1,y1,z1) до точки D (x2,y2,z2) имеет вид: || x2-x1 y2-y1 z2-z1 ||
Примени это к заданым точкам – получишь векторы.

Построить параллелепипед ( с ненулевым объёмом, надо полагать) можно, если они не лежат в одной плоскости. Иначе – образуют базис в 3D пространстве.

Убедиться можно либо доказав их линейную независимость, либо посчитав смешанное произведение. Формулы в учебнике и в инете есть. Координаты есть из предыдущего шага.

Собственно, для вычисления объёма нужно то же векторное произведение.

Видео:№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Описание файла

PDF-файл из архива «Домашнее задание по аналитической геометрии (модуль №1)», который расположен в категории «9 вариант». Всё это находится в предмете «аналитическая геометрия» из первого семестра, которые можно найти в файловом архиве МГТУ им. Баумана. Не смотря на прямую связь этого архива с МГТУ им. Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «курсовые/домашние работы», в предмете «аналитическая геометрия» в общих файлах.

Видео:№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

Просмотр PDF-файла онлайн

Видео:№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

Текст из PDF

1 курс 1 семестрМодуль 1. Векторная алгебра. Прямая и плоскость в пространстве.Домашнее задание N 1.Дано: точки A, B, D, A1 ; числа a, b; угол ϕ.Задание:1. Найти длину вектора |m + n|, если m = p + aq, n = bp + q,где p и q — единичные векторы, угол между которыми равен ϕ.−→2. Найти координаты точки М , делящей вектор AB в отношении a : 1.−→ −−→3. Проверить, можно ли на векторах AB и AD построить параллелограмм.Если да, то найти длины сторон параллелограмма.4. Найти углы между диагоналями параллелограмма ABCD.5. Найти площадь параллелограмма ABCD.−→ −−→ −−→6.

Убедиться, что на векторах AB, AD, AA1 можно построить параллелепипед.Найти объем этого параллелепипеда и длину его высоты.−−→7. Найти координаты вектора AH, направленного по высоте параллелепипеда,проведенной из точки A к плоскости основания A1 B1 C1 D1 , координаты точки H−−→и координаты единичного вектора, совпадающего по направлению с вектором AH.−−→−→ −−→ −−→8. Найти разложение вектора AH по векторам AB, AD, AA1 .−−→−−→9. Найти проекцию вектора AH на вектор AA1 .10. Написать уравнения плоскостей:а) P , проходящей через точки A, B, D;б) P1 , проходящей через точку A и прямую A1 B1 ;в) P2 , проходящей через точку A1 параллельно плоскости P ;г) P3 , содержащей прямые AD и AA1 ;д) P4 , проходящей через точки A и C1 , перпендикулярно плоскости P .11.

Найти расстояние между прямыми, на которых лежат ребра AB и CC1 ;написать канонические и параметрические уравнения общего к ним перпендикуляра.12. Найти точку A2 , симметричную точке A1 относительно плоскости основанияABCD.13. Найти угол между прямой, на которой лежит диагональ A1 C и плоскостьюоснования ABCD.14. Найти острый угол между плоскостями ABCD (плоскость P ) и ABB1 A1(плоскость P1 ).Примечание.Зачётное число задач – 11 из 14.Оценка: 10 баллов – за 11 правильно решённых задач; 3 балла – за остальныерешённые задачи ДЗ.Сроки выполнения: выдача – 2 неделя; приём – 9 неделя.1Варианты задания1234567891011121314151617181920212223242526272829303132ABDA1abϕ1, 0, 02, −1, 31, 0, 11, 1, 10, 0, −12, 0, 10, 1, 03, −2, 21, 2, 30, 1, 00, 1, 03, −1, 10, 3, 03, 1, 20, 3, 2−1, 2, 00, 3, −23, 1, 11, 2, 02, 2, 30, 1, 00, 2, 10, 2, −32, 2, 12, 0, 13, −1, 03, 2, 02, 3, 10, 1, 2−1, 2, 2−1, 4, 20, 3, 21, 2, 03, −2, 21, 2, 30, 1, 00, 1, 03, −1, 11, 0, 03, 1, 20, 3, 2−1, 2, 00, 3, −23, 1, 10, 1, 02, 2, 30, 1, 00, 2, 10, 2, −32, 2, 10, 3, 02, −1, 31, 0, 11, 1, 10, 0, −12, 0, 13, −1, 03, 2, 02, 3, 12, 0, 10, 3, 20, 1, 2−1, 2, 2−1, 4, 20, 1, 02, 2, 30, 1, 00, 2, 10, 2, −32, 2, 10, 3, 02, −1, 31, 0, 11, 1, 10, 0, −12, 0, 11, 2, 03, −2, 21, 2, 30, 1, 00, 1, 03, −1, 11, 0, 03, 1, 20, 3, 2−1, 2, 00, 3, −23, 1, 12, 3, 12, 0, 13, −1, 03, 2, 0−1, 2, 2−1, 4, 20, 3, 20, 1, 20, 1, 22, 0, 11, 0, 22, 0, 31, 0, 20, −2, 3−1, 2, 23, −1, 01, 2, 41, 0, 21, 1, 31, −3, 3−1, 4, 23, 2, 00, 3, 30, 1, 21, 3, 11, −1, 30, 3, 22, 3, 10, 1, 11, 1, 31, 2, 00, 0, 32, −1, 33, −2, 23, 1, 22, 2, 31, 0, 00, 1, 00, 3, 01, 2, 051234567891071213141516171819202122232425262728293031−6−1−1−1−1−1−1−1−1−1−119−1−1−1−1−1−1−1−1−1−1−1−1−1−1−1−1−1−1−1−10π/6π/22π/311π/65π/67π/611π/63π/24π/3π/6ππ/34π/35π/67π/6π/3π/4π/35π/3π/211π/6π/47π/4π/2π3π/45π/42π/34π/35π/67π/62.

Видео:№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

Смешанное, векторное и скалярное произведение векторов

Задача:

Дан параллелепипед ABCDA₁B₁C₁D₁, построен на векторах AB(4,3,0), AD(2,1,2) и AA₁(-3,-2,5).
Найти:

Решение:

• а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA₁). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.

Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
V_ABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. S_ABCD= |[AB AD]|.

Теперь найдём модуль этого вектора:

S_ADD1A1= |[AD AA₁]|=√(81+256+1)=13√2.

г) Косинус угла λ₁, между ребром AB и диагональю B₁D будем высчитывать с помощью скалярного произведения векторов

cos(λ1)	=	(AB B1D) |AB| * |B1D|	.

Координаты вектора AB мы имеем, от вектор B₁D надо найти. Для этого используем следующую формулу:
B₁D = B₁A₁ + A₁A + AD = — AB — AA₁ + AD₁ = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B₁D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B₁D:
|AB|=√(16+9+0)=5, |B₁D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B₁D, (AB B₁D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:

cos(λ1)	=	4 5√(10)	=	2√(10) 25	.

д) Что бы найти cos(λ₂), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD₁A₁ мы можем взять вектор [AD AA₁], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.

cos(λ2)	=	6*9 + (-8)*(-16) + (-2)*(-1) 2√(26) * 13√(2)	=	46√(13) 169	.

Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD₁A₁.

Видео:№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Видео:№361. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. Разложите векторыСкачать

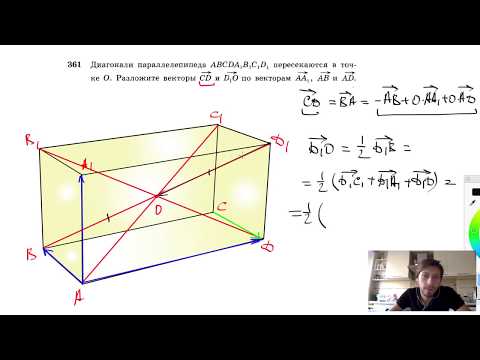
Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Видео:1. Векторы и параллелограмм задачи №1Скачать

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Доказательство.

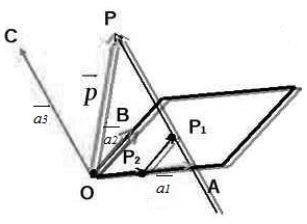
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:

[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow

=overrightarrow]

Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

🔍 Видео

Правило параллелепипеда для векторовСкачать

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

§20 Нахождение объёма параллелипипедаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

№76. Дан параллелепипед ABCDA1B1C1D1. Докажите, что AC||A1C1 и BD||B1D1.Скачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

№368. Точки М и N являются серединами ребер АВ и A1D1 параллелепипеда ABCDA1B1C1D1.Скачать

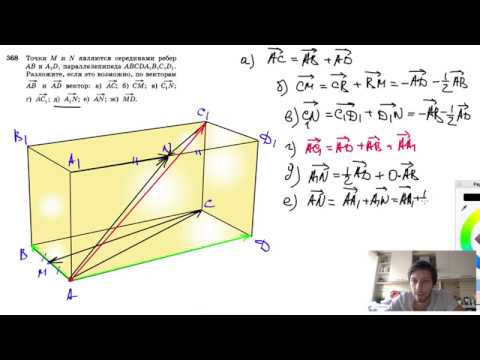
№116. Дан параллелепипед ABCDA1B1C1D1. Докажите, что: а) DC⊥B1C1, и AB⊥A1DСкачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

№337. Упростите выражение: a) OP - EP + KD - KA; б) AD + MP + EK - EP - MD;Скачать

№357. Даны параллелограммы ABCD и AB1C1D1. Докажите, что векторы ВВ1, СС1 и DD1 компланарны.Скачать